Борис Ротгауз

![]()
Дюссельдорф 2003
НАЧАЛА НЕТРАДИЦИОННОЙ ЭВОЛЮЦИИ ФИЗИКИ.
Глава 1. Краткий исторический
экскурс в традиционную физику
Глава
2. Попытка философского осмысливания естествознания
1 Принципы
определения используемых понятий
4
Дуалистическая пара понятий: объекты и субъекты
6 Математические
и физические объекты
7 Относительные
состояния и предшествование
Глава 3. Суть аксиоматического
подхода к физике
1
Фундаментальные
характеристики физического объекта
3
Точки и пространственная
удаленность их
4
Элементарные изменения и их
наблюдение
6
Непрерывность наблюдения и
скорость изменения объектов
9
Конечные и бесконечные
расстояния – излучение и поглощение
12 Энергия
– фундаментальная интегральная характеристика системы объектов
13 Ограниченность относительной скорости
объектов и универсальный сигнал
14 Объекты
как колебательные системы
15 Гравитационное
взаимодействие и два состояния тепловой смерти вселенной
16 Радиально-тангенциальное взаимодействие
объектов
В теоретической
физике для продвижения вперед поиск логической последовательности всегда был
важнее, чем экспериментальные результаты. Многие прекрасные теории отвергались,
т.к. не согласовывались с наблюдениями, но я не знаю ни одной серьезной теории,
которая бы продвинулась только на основе эксперимента. Теория всегда приходит
первой, она возникает из желания получить стройную математическую модель.
Стивен Хокинг, Черные дыры и молодые вселенные. Санкт-Петербург, Амфора/Эврика, 2001, стр. 50
Возможно,
ли строить физику полностью аксиоматически, т.е. все фундаментальные законы
физики выводить как теоремы исходя из небольшого числа априори принятых аксиом?
Или физика должна остаться эмпирической, т.е. такой, в которой каждый
фундаментальный закон постулируются на основании соответствующих наблюдаемых
явлений. Необходимо ли сохранять фактически оформившееся в начале ХХ века
разбиения физики на две физики - на макро и на микро физику, существование
которых обусловлено представлениями о континуальности изменений макро объектов
и дискретности изменений микро объектов? Или возможна единая физика, исходные
понятия которой обусловлены фактическим
существованием лишь дискретности всех физических явлений, вне
зависимости от возможностей различного восприятия их. Должны ли исходные
понятия физики быть математическими – таковыми, например, в традиционной физике
являются «пространственно-временной континуум», «системы отсчета» и др. или эти
понятия должны быть физическими – реальными, т.е. основанными на непосредственно
наблюдаемых и экспериментально реализуемых явлениях? Существует ли взаимодействия
между физическими объектами, и являются
ли они дальнодействующими или близкодействующими? С чем связана имеющаяся в
физике проблема необратимости времени – инвариантность принятых фундаментальных законов физики относительно
знака времени и несимметричность наблюдаемых физических явлений во времени?
Размышления над этими и подобными вопросами вынуждают радикально изменить
традиционную физику.
Прежде
всего, следует сказать, что настоящая брошюра рассчитана на читателей,
интересующихся проблемами естествознания в широком смысле этого слова. Но
главным образом, брошюра рассчитана на читателей, интересующихся проблемами
физики и математики, лежащими в основе естествознания. Является ли брошюра
научно-популярной или она ориентирована только на профессиональных физиков?
Если исходить из того, что для чтения и полного понимания содержания брошюры
достаточно знаний физики в объеме гимназии (в крайнем случае, начальных курсов
не гуманитарных высших учебных заведений – необходимые дополнительные сведения
имеются в брошюре), то брошюра может считаться научно-популярной. Но, если
учесть, что в брошюре приведен принципиально новый подход к построению физики,
основанный на строгом соответствии методов аналитического описания явлений
природы – фактически реализуемым способам наблюдения за ними, то брошюра,
несомненно, представит профессиональный интерес для специалистов. В
соответствии с названием этой брошюры, в ней основное внимание уделено
изложению идей (начал или исходных положений) нетрадиционного построения физики
и намечены пути практической реализации такого построения. При этом наиболее важным
представляется корректное определение исходных принципов и положений, а также
строгие логичные рассуждения при выводе лишь фундаментальных и общеизвестных
закономерностей, экспериментальное существование которых неоднократно и достоверно
подтверждено. Что касается всех технических деталей построения теоретической
физики в значительно большем объеме чем приведено в брошюре, не говоря уже об
объеме, в котором существует современная традиционная физика, то такое
построение может быть выполнено только достаточным числом ученых (может быть
даже не одного поколения), разделяющих ниже приведенные парадигмы нетрадиционного
подхода.
Изложенный
в брошюре подход, позволяет существенно продвинуться в понимании и решении фундаментальных проблем
физики (естествознания). Например, таких проблем как – объективность и субъективность
причинно-следственных отношений в физике; полнота и точность фундаментальных
законов; что следует понимать под взаимодействием физических объектов и
является ли оно «дальнодействующим» или «близкодействующим»; проявления
необратимости физических явлений и ряда других принципиальных вопросов, о которых речь идет
ниже. Представляется, что эти проблемы имеют системный характер и,
следовательно, могут быть преодолены путем радикальных изменений физики на
фундаментальном уровне. Необходимо иметь ввиду, что как показывает практика,
сколько-нибудь существенные изменения физики обычно не вызывают энтузиазма и единодушного
восприятия их на первых порах, в силу свойственного каждому индивиду и обществу
в целом здорового консерватизма. Тем более, если речь идет о ниже изложенных
радикальных изменениях, затрагивающих, в том числе, и философские вопросы
естествознания. Вместе с тем, необходимо напомнить, что еще не доказана теорема
единственности для какого-нибудь одного подхода к физике и вряд ли когда-нибудь
такая теорема будет доказана в будущем. Скорее всего, прав был выдающийся физик
ХХ века Р. Фейнман, утверждавший что: «Одна из особенностей природы - многообразие
возможных схем ее толкования» см. [3] стр. 55. Таким образом,
следует поощрять новые подходы к физике, особенно если они преследуют не просто
цели иного изложения уже известных положений, а расширяют возможности описания
большего числа явлений с единых позиций. Желательны и дискуссии по новым
подходам с участием как можно большего числа, как физиков, так и философов.
Ведь говорят, что истина рождается в споре. Но при этом спор не должен вестись
ради спора, т.к. в схоластических спорах истина не только не рождается, но и
может умереть.
Прежде
чем приступить непосредственно к изложению содержания брошюры, сформулируем
замечание философского характера близкое к направлению позитивизма, которому
будем следовать в той или иной степени на протяжении всего изложения. Суть этого
замечания в том, что ответы на многочисленные вопросы, которые мы задаем
природе о способах ее устройства, нужно искать не только, и даже не столько в самой
природе, сколько в нас самих – в субъектах (если только допустимо разделять
субъекты и природу), формулирующих эти вопросы. Заметим, что иногда объекты и
субъекты называют соответственно «неживой» и «живой» природой. И даже можно
сказать, что, в конечном счете, искать такие ответы нужно и в тех и в других,
поскольку объекты и субъекты не являются абсолютно несвязанными и независимыми
друг от друга, о чем подробнее говорится ниже при определении этих понятий. Сходных
взглядов на возможные причины того или иного устройства природы придерживались
и некоторые философы в прошлом. В частности Декарт, вообще считал, что любая
причинно-следственная связь – не более чем теорема, выводимая из ранее
доказанных теорем и аксиом. Causa
sive ratio –
причина есть не что иное, как разум. Тем самым причина считалась субъективной.
Галилей тоже настоятельно советовал естествоиспытателям не рассуждать о причинах
происхождения физических явлений, а описывать их математически (количественно).
Другими словами – не считать природу абсолютно объективной, и не пытаться
познать ее свойства как независящие от субъектов. Эта основополагающая идея
противоречила взглядам предшествующих философов, например, Аристотеля и его
последователей, которые истинную задачу науки видели в попытках найти
объективные физические объяснения наблюдаемых явлений. Как стало в дальнейшем
очевидным, взгляды Галилея явились глубокой и плодотворной идеей методологии,
которой физика придерживается до настоящего времени. Имеется в виду, что хотя до
сих пор отсутствует удовлетворительное физическое понимание и объяснение природы
гравитационных и всех других взаимодействий, но мы на практике широко
пользуемся основанными на них явлениями и можем с большой точностью прогнозировать
проявление их действий исходя из своих субъективных моделей. Здесь по сути
физика заменяется математикой, если рассматривать эти две науки как не
связанные друг с другом, что, строго говоря, представляется неправомерным.
Исходя из выше сказанного, предлагается строить физику
полностью аксиоматически. При таком подходе необходимым условием является как
можно более строгое предварительное определение того, что должно явиться предметом рассмотрения физики, в частности – определение физических объектов. А также того, каким
образом это определение и определения других терминов и понятий должны быть
получены. Необходимо также, чтобы такие определения осуществлялись только в
рамках физики и были бы исходными понятиями, т.е. чтобы при этом не использовались
понятия других наук. Примером для подражания в этом деле может служить
математика,
которая определяет предмет своего рассмотрения – математические понятия и объекты
– непосредственно как исходные, т.е. не использует для их определения другие,
более исходные (тем более не являющиеся математическими) понятия и объекты.
Поэтому, все применяемые в математике понятия и объекты являются достаточно
хорошо осмысливаемыми и практически не допускающими принципиальных
неоднозначностей. В частности, таким
образом поступил гениальный Евклид, предваряя построение геометрии определением используемых им понятий
«точка», «линия», «прямая», «окружность», «плоскость» и др. с тем, чтобы
исключить неоднозначное осмысливание этих понятий и всей своей геометрии.
Только в первой книге его знаменитого «Начала», всего их 13, приведено 23
определения, см. [4]. Затем для этих, уже определенных
математических понятий/объектов, было сформулировано минимальное число
независимых друг от друга аксиом (очевидных свойств) исходя из которых, можно
выводить путем строгих логичных рассуждений, любые другие далеко неочевидные
свойства.
Исходные
физические понятия должны быть основаны только на непосредственно
воспринимаемых опытных (физических) данных, а не частично на них и частично на математических
понятиях, как это имеет место сейчас. Имеется в виду, что не надо, как сейчас поступают
в традиционной физике, вначале вводить в качестве исходных понятий такие чисто
математические, а нефизические понятия как безграничное пространство и бесконечное
время (четырехмерный пространственно-временной континуум); системы отсчета; силы
и силовые поля; взаимодействия и др., а затем, оперируя этими понятиями определять
физические объекты. Кстати все эти исходные математические понятия вводятся и
осмысливаются с использованием (явным или неявным образом) априори существующее
физического понятия «материальный объект», и в этой связи не понятно, зачем
надо использовать понятия пространство и время для того, чтобы определять уже
осмысленное понятие материальный или физический объект. Определенные таким
образом выше упомянутые исходные понятия традиционной физики являются
интуитивными – не имеющими строгого экспериментального обоснования, и поэтому
они сложны для осмысливания и, как следствие, приводят к неоднозначному восприятию
законов природы. Для придания большей весомости высказанной мысли о сложности
осмысливания исходных понятий традиционной физики (многие физики ее стесняются
высказывать), сошлемся на мнение авторитетного ученого-физика, лауреата
Нобелевской премии по физике, Стивена Хокинга, которого трудно заподозрить в
недостаточно глубоком восприятии физики:
«Четырехмерное пространство представить
себе не возможно. Лично я с трудом представляю себе даже трехмерное
пространство», см. [25] стр.44. Однозначное восприятие и осмысливание того,
что такое физический/материальный объект у человечества было (не только у
физиков) еще до формулировки этих математических понятий, и до сих пор у
большинства оно продолжает иметь место практически в неизменном виде без использования
этих понятий. Физический объект это простейшее понятие, попытка формализовать
которое предпринята ниже. И, если исходить из этого очевидного положения,
которое ниже принято в качестве постулата, то не нужно вводить более простые
понятия для того, чтобы с их помощью воспринимать и определять это простейшее
понятие. Таких более, простых понятий в данном случае просто не существует по
определению. Как еще указывал Аристотель, простейшие (неопределяемые) понятия
должны иметь место, т.к. в противном случае определение любых других понятий
было бы бесконечным процессом и, следовательно, оно не имело бы смысла. Это
замечание справедливо и для постулатов, истинность которых не нужно (нельзя)
доказывать, т.к. иначе все доказательства были бы бесконечными – бессмысленными.
Если
отказаться от использования понятий пространство и время («пространственно-временной
континуум») как самостоятельных понятий для утверждений о возможности
изменения/сохранения в них физических объектов, то отпадает необходимость априори
постулировать существование различных «сортов» физических (материальных) объектов
и разных фундаментальных закономерностей для них, как это имеет место в
традиционной физике. Предлагается исходить из единого очевидного «свойства»,
справедливого для любых материальных объектов, позволяющего, как показано ниже,
выводить из него в виде следствий (теорем) соответствующие фундаментальные закономерности
в поведении объектов. Фактически это означает, что никаких специальных и
объективных «свойств», кроме «свойства существовать» – быть наблюдаемыми
субъектами, физическим объектам приписывать не надо. Сказанное означает, что не
нужно отдельно постулировать существование объектов, способных притягиваться и
отталкиваться друг от друга с большой интенсивностью, так называемых электрических
зарядов, и отдельно существование электрически нейтральных объектов, способных
только притягиваться друг к другу с гораздо меньшей интенсивностью, так
называемых гравитационных масс. Как показано ниже, наблюдаемые различия в поведении
объектов (различие восприятий их), может быть объяснено лишь различием количества
и расположения материальных объектов, учитываемых субъектом при наблюдениях физических
явлений. Практически это означает, что не надо априори постулировать существование
и аналитический вид различных и полностью объективных (независящих от
субъектов) целенаправленных взаимных действий физических объектов друг на друга
– так называемых гравитационных, электромагнитных, сильных, слабых и др.
взаимодействий. Все эти взаимодействия могут быть получены как следствия (как
теоремы) исходных положений. Тем самым, отпадает необходимость затрачивать не
малые материальные и другие ресурсы на постановку дорогостоящих экспериментов,
направленных на поиск физических носителей взаимных действий и на выяснение механизмов
реализации их. Опыт (эксперимент) служит лишь критерием истинности, как
исходных положений, так и получаемых следствий. Таким образом, все ниже
изложенное « ...находится в тесной связи
с «основным принципом теории познания»:
объективная картина мира не должна содержать ничего такого, что в принципе не
могло бы быть проверенно на опыте». Именно так этот принцип назван и сформулирован
одним из самых выдающихся ученых и мыслителей ХX века Германом Вейлем (1885
-1955), известным своими работами в области математического анализа, теории
чисел, дифференциальной геометрии, оснований математики и логики, теории относительности
и квантовой механики, см. [1] стр. 197. Выделение в этой цитате мое (Б. Р.).
В
рамках предлагаемого подхода не нужно специально постулировать для макро и
микро объектов возможность соответственно непрерывного и дискретного изменения
их. Не требует предлагаемый подход, как уже указывалось, и использования не
строго определенных и поэтому сложных для осмысливания нефизических понятий,
таких как пространственно-временной континуум, система отсчета, поле,
взаимодействие и т.п. Достаточно исходить из априори существующей для субъектов
возможности воспринимать и осмысливать только в единстве систему следующих трех
фундаментальных физических понятий/ощущений – протяженность, продолжительность
и материальность, и характеризовать этой трехкомпонентной системой
понятий только ограниченные физические объекты и конечные системы их. Заметим,
что понятие материальность позволяет воспринимать лишь количество
рассматриваемых объектов
или возможность считать их. Иной парадигмы
придерживается классическая физика, которая считает первые два понятия –
пространство и время как континуальные (не дискретные) понятия, не связанные между
собой – осмысливает эти безграничные понятия фактически отдельно друг от друга
и от понятия материальность. Релятивистская физика считает едиными (не
допускающими раздельного рассмотрения) только первые два понятия, и осмысливает
их тоже как безграничный континуум – пространственно-временной континуум.
Материя непосредственно не задействована в определениях этих традиционных
континуумов. В рамках предлагаемого подхода легко прослеживается то, что
математика и физика должны иметь одинаковые не только идеологию построения, основанную
на понятии предшествования, но и конструктивную методологию, и поэтому в
обобщенном смысле математика может рассматриваться как частный/ предельный
случай физики. Показывается, что фундаментальные законы традиционной физики (классической
и релятивистской) является лишь вторым приближением в описании мироздания, и
указано как могут быть получены дальнейшие приближения. Кроме этого, появляется
возможность решить и не менее трудную
проблему, носящую название «Стрела Времени» или временная необратимость, т.е.
объяснить, почему все принятые фундаментальные законы традиционной физики
симметричны относительно обращения времени, а практически все физические
явления нет.
Глава 1. Краткий исторический экскурс в традиционную физику
Прежде
чем излагать подходы к аксиоматическому построению физики, целесообразно хотя
бы кратко проследить этапы развития традиционной (эмпирической) физики и, в
частности, гносеологию основных применяемых в физических понятий. Это позволит
лучше критически осмыслить эти понятия и предложить наиболее оптимальные
формулировки аксиом физики.
Часто
отцом физики называют выдающегося ученого и философа древней Греции, автора
сочинений «Физика», «Метафизика», основоположника формальной логики, учения о
движении, об этике и человеке как общественном существе, о государстве и др. -
Аристотеля (384 – 322 гг. до новой эры). Согласно ему физика это наука об
основных закономерностях («первичных
причинах»), принципах («первых
началах») природы и ее «элементов».
Его книга, называемая «Физикой» является скорее философским трактатом, чем
книгой по естествознанию. Движение состоит в уничтожении и возникновении вещей,
в их росте или изменении. Аристотель говорит о естественном движении как
исходном понятии физики. Тела, занимающие места, отличные от естественных мест,
получают импульсы, а оказавшиеся на своих естественных местах, - не получают.
Каждому телу свойственно определенное место: легкие тела – наверху, тяжелые –
внизу. Тела стремятся к своим местам и такое их движение – легких тел вверх,
тяжелых – вниз не требует объяснения, т.к. оно является естественным. При этом
Аристотель писал: «Я именую легким то,
что всегда стремится двигаться наверх, и тяжелым то, что всегда стремится
двигаться вниз при отсутствии какого-либо вмешательства». Другие движения, не относящиеся к
естественным движениям, являются искусственными – насильственными и для
объяснения, почему они имеют место, требуется указание причин, которые
Аристотель называл силами. Вселенная Аристотеля была замкнута, ограничена
снаружи небесной сферой и заполнена
небесной субстанцией. В центре Вселенной находилась Земля. Движение звезд и
небесных тел по небесному своду считалось
естественным. Обратимся еще раз к Аристотелю: «...естественное движение Земли, так же как движение отдельных ее
частей, направлены к центру Вселенной: вот почему сейчас Земля находится в
центре… Легкие тела, подобные огню, движение которых противоположно движению тяжелых
тел, стремятся к краю области, окружающей центр». Аристотель отрицал
пустоту, или однородное пространство. Естественное движение по Аристотелю не
может существовать, если все точки пространства равноправны. Для такого
пространства «...никто не может сказать,
почему тело, приведенное в движение, где-нибудь остановится, ибо - почему оно
должно остановиться здесь, а не там?». Аналогично отрицанию понятия пустого
пространства, в противоположность взглядам атомистов древней Греции (Демокрита,
Эпикура и др.), Аристотель не признавал существование понятия времени,
независимо от происходящих явлений. С его точки зрения время не существует без
каких-либо изменений. Он писал: «Если бы
«теперь» не было бы каждый раз другим, а оставалось тождественным и единым,
времени не было бы». Принципиальными для нашего изложения в этих
представлениях являются следующие два положения. Во-первых, допускались как
естественные движения, не требующие указания причин их существования, так и
искусственные (насильственные) движения, возникающие только при действии
внешних сил. Во-вторых, все движения (как искусственные, так и естественные)
совершались относительно другого конкретного тела. Для естественных движений – таковым была Земля, считавшаяся абсолютно неподвижной
и определяемой понятия «вверх и вниз». Заметим, что представления Аристотеля о
геоцентрической Вселенной принципиально отличались от первых идей
гелиоцентрической системы мира Аристарха (IV – III вв. до новой
эры). Для схоластов, приверженцев Аристотеля, положения этой физики считались
вершиной человеческих знаний. В средние века это учение было канонизировано
церковью, что, по мнению некоторых ученых, превратилось на длительном этапе в
тормоз развитию физики и астрономии.
После
того как физика Аристотеля стала известна в Европе, она начала подвергаться
критике со стороны многих ученых. Член Парижской школы Никола Оресм, живший в
четырнадцатом веке, оспаривал исключительность положения Земли. Он считал, что
движения звезд и Земли относительны: возможно рассмотрение неподвижности звезд
и движение Земли относительно них и наоборот – в любом случае эффект будет
одинаков. Более того, некоторые ученые (например, Пьер Раме) вообще считали,
что вся физика Аристотеля не научна. Заметим, что сам Аристотель к своим
предшественникам относился тоже без должного почтения и подвергал
беспристрастной критике не только их, но и своих учителей. Именно благодаря
этому, мы осведомлены о многих ранних писателях Греции, чьи воззрения изложил
Аристотель, чтобы опровергнуть их. Есть предположение, что изречение «Aims Plato, sedmagis amica verities» («Платон
мне друг, но истина дороже»)
принадлежит Аристотелю. Платон (428 или 427 до н. э. – 348 или 347) говорил о
своем лучшем и наиболее выдающемся ученике, что он ведет себя подобно молодому
жеребцу, лягающему свою мать.
Многовековая
критика идей Аристотеля вылилась в пересмотр проблемы движения и подготовила
почву для создания принципиально новой и более рациональной физики. Коренным
образом изменилась сама Вселенная. Н. Коперник (1473 – 1543) поместил Солнце в
центр ее, отведя Земле более скромную роль одной из планет. Джордано Бруно
(1548 – 1600) пошел дальше - разбил небесную сферу и, будучи сторонником
бесконечного пространства, он сделал Вселенную неограниченной. Земля и Солнце
оказались затерянными среди бесчисленного количества других планет и солнц. За
такие еретические взгляды Джордано Бруно был сожжен инквизицией на костре.
Гассенди (1592 – 1655) - Мольер и Сирано де Бержерак были его студентами -
высказал предположения, восходящие к
атомизму Демокрита и Лукреция, о том, что мир состоит из атомов и их комбинаций,
находящихся в пустоте. Ни какие тела больше не стремятся занять «естественное» положение в пространстве,
а двигаются по строгим объективным законам, не зависящим от бога, хотя
первопричиной всех вещей мог быть бог. Взгляды Гассенди были не менее еретическими, чем взгляда
Бруно, однако как человек он был более покладистым, и ни кому не могло прийти в
голову сжечь Гассенди на костре, поскольку он в юности имел много друзей, был
скромным и регулярно посещал церковь.
Дальнейшее
развитие физики было связано с тем, что В. Гильбертом (1540 – 1603) в его
трактате «De magnete» было высказано предположение «…что, материя может взаимодействовать лишь путем соприкосновения».
В частности, притяжение двух тел, плавающих в жидкости, есть результат действия
этой жидкости. Эти идеи В. Гильберта: действие через контакт и объяснение
притяжения действием жидкости,– являются
фундаментальными идеями системы Рене Декарта (1596 - 1650), хотя сам он
не признавал себя чем-нибудь обязанным своему предшественнику. Система
философских и научных взглядов Декарта получила название картезианства, т.к.
Декарт подписывал свои сочинения латинизированной формой своей фамилии – Картезиус.
Картезианское мировоззрение имело широкое распространение, особенно во Франции,
во второй половине ХVII в. и в первой половине ХVIII в. и именно там существовали горячие последователи
этого учения. Можно сказать, что Парижская академия наук являлась в те времена
оплотом картезианства. Дальнодействие – действие на расстоянии в пустоте –
отвергалось философией Декарта и всей его физической теорией мироздания. Декарт
никогда не допускал даже мысли о существовании пустоты. Известны его
двусмысленные высказывания о том, что «вакуум
существует только в голове Паскаля». Само мировое пространство считалось
заполненным особым легким, подвижным веществом, образующим гигантские вихри. В
центральной части каждого такого вихря сгущается светоносное вещество,
образующее небесные светила. Так, солнечный вихрь увлекает в своем движении все
планеты с их спутниками, а вихрь, окружающий Землю, вовлекает в круговое
движение вокруг Земли ее спутник Луну. Аналогичные явления имеют место и для
других планет и их спутников. Эти вихревые потоки увлекают и приводят в
движение все тела, попадающие в сферу вихря, причем в каждом вихре тело,
находящееся ближе к центру, вращается вокруг него быстрее, чем более далекое.
Именно этим Декарт объяснял тот факт, что период обращения планет вокруг Солнца
тем короче, чем ближе планеты к Солнцу. Взаимодействие тел, в частности
приведение их в состояние движения, может происходить только при непосредственном
их соприкосновении. Такое соприкосновение может осуществляться и посредством
промежуточной среды, роль которой у Декарта выполняли вихри. Таким образом,
примитивная с современных позиций материалистическая точка зрения на
взаимодействие тел выражена в мировоззрении Декарта наиболее четко по сравнению
с его предшественниками. Но при этом эта теория не смогла достаточно внятно объяснить,
почему траектории планет солнечной системы являются не круговыми, а эллиптическими
и соответствующими законам И. Кеплера (1571 – 1630), ставшими известными в то
время. Взгляды Кеплера существенно отличались от картезианской теории тяжести.
Кеплером, по-видимому, впервые высказана мысль о тяжести как о взаимном притяжении
между тяжелыми телами и Землей. Такие представления о взаимном притяжении тел
было новым, и в дальнейшем явились основой, на которой была построена теория
гравитации И. Ньютона (1642 – 1727). Между кеплеровым притяжением и теорией
Платона, принятой Коперником и Г. Галилеем (1564 – 1642), имелось очевидное
различие. Последняя теория предполагала, что тела имеют естественную склонность
соединяться, и источником этого является внутренний инстинкт тел. Он не зависел
ни от чего внешнего и поэтому по силе инстинкт был постоянным. Кеплерова теория
располагала источник притяжения вне тела и тем самым позволяла объяснить
изменение тяжести с расстоянием.
Принципиально
новая идеология построения физики, которая в определенной мере сохраняется до
сих пор, связана с именами Г. Галилея и И. Ньютона. Первому принадлежит
важнейший принцип, известный под названием принцип относительности Галилея, на
котором основана вся современная физика и который был распространен А.
Эйнштейном (1879 – 1955) на все (не только механические) законы природы. В
своей книге «Диалог о двух главнейших системах мира – птолемеевой и коперниковой»
Галилей писал, приводя наблюдения в закрытой каюте корабля. «Заставьте теперь корабль двигаться с любой
скоростью, и тогда (если только движение будет равномерным и без качки в ту или
иную сторону) во всех названных явлениях вы не обнаружите ни малейшего
изменения, и ни по одному из них не сможете установить - движется ли корабль
или стоит неподвижно..». Ни менее важна заслуга Галилея и в том, что он
впервые показал, что тяжелые и легкие тела падают на землю по одним и тем же
законам. Существует легенда, что для того чтобы люди сами могли убедиться в
этом, Галилей в присутствии публики сбрасывал с наклонной Пизанской башни две
сферы, массы которых существенно отличались друг от друга, и все могли наблюдать,
как эти сферы в процессе падения все
время остаются рядом и падают на землю одновременно. Видимое в некоторых
случаях различие в падении таких тел связано только с сопротивлением воздуха.
Говорят, что когда скептически настроенные ученые – современники Галилея –
увидели своими глазами, как в стеклянной трубке, из которой выкачан воздух,
металлический шарик и пушинка падают совершенно одинаково, то не все из них
поверили своим глазам. Предубеждения в справедливости указанного положения
сохранялись, даже не смотря на приведенные в «Беседах» Галилея несложные
логичные рассуждения о падении тяжелого камня. В таких рассуждениях камень
можно представить как состоящий из двух частей – тяжелой и легкой - и,
следовательно, при падении эти две части должны были бы удаляться друг от
друга, т.е. камень должен был бы распадаться на части. Именно универсальность
(одинаковость) ускорения свободного падения различных тел в гравитационном
поле, а также принцип относительности стали краеугольными камнями в обосновании
теории относительности А. Эйнштейна.
Далее,
именно Галилеем почти через две тысячи лет после Аристотеля экспериментально
доказано, что скорость падающего тела в пустоте пропорциональна не высоте
падения, как думали ранее, а времени падения. На современном языке это
означает, что остается постоянным ускорение падения, а не скорость. Но это
имеет место только для тех случаев (именно они были доступны Галилею), при
которых сила притяжения остается постоянной. Интересно, что все эти, в высшей
степени, фундаментальные результаты были получены Галилеем на основе
примитивных опытных данных (по сравнению с современной техникой физических
экспериментов). Например, поскольку тела падали достаточно «быстро» с точки
зрения способов замера времени, которыми
располагал Галилей, то для «ослабления» гравитационного влияния Галилей
наблюдал за шарами, катящимися по наклонным плоскостям. В те времена еще
хронометров не существовало (чаще всего их заменял пульс), и Галилей измерял
отрезки времени путем взвешивания воды, вытекающей из большого сосуда с узким
горлышком. Он установил, что шар, начавший движение по наклонной плоскости с
какой-то высоты, подымится по другой наклонной плоскости на такую же высоту вне
зависимости от угла наклона этой второй плоскости. В случае если вторая
плоскость является горизонтальной, то шар будет катиться безостановочно, если
на него не будут действовать силы трения. Другими словами, в случае отсутствия
сил, действующих на тело, оно будет сохранять естественное движение как
прямолинейное и равномерное. Это положение, принятое Ньютоном в качестве
первого из трех его законов механики, и называемое законом инерции, было революцией
в механике, поскольку со времен Аристотеля считалось, что тело неподверженное
никакому влиянию сил должно, в конце концов, прийти к своему естественному
состоянию – покою. Но какой смысл нужно вкладывать в понятие сила? Предоставим
здесь слово Анри Пуанкаре (1854 – 1912 гг.) французскому математику, физику и
философу, одному из создателей частной теории относительности и релятивистской
динамики: «Что такое сила? Это отвечает
Лагранж, причина, производящая или стремящаяся произвести движение тела. Это,
скажет Кирхгоф, произведение массы на ускорение. Но тогда почему не сказать,
что масса это частное от деления силы на ускорение. Что такое масса? Это
отвечает Ньютон произведение объема на его плотность. Лучше сказать, возражают
Томсон и Тэт, что плотность есть частное от деления массы на объем. Эти
трудности непреодолимы. Определяя силу как причину движения, мы становимся на
почву метафизики, и если бы таким определением пришлось удовлетвориться, то оно
было бы абсолютно бесплодно. Чтобы определение могло быть к чему-нибудь
пригодно, - оно должно научить нас измерению силы; к тому же этого условия и
достаточно; нет никакой необходимости, чтобы определение учило нас тому, что
такое сила сама по себе, или тому, есть ли она причина или следствие движения»,
см. [11] стр. 68.
Весьма
важным для последующего развития физики было и решение Галилеем задачи о
движении снаряда (ядра). До этого относительно формы траектории ядра делались
самые разные предположения. Так еще во второй половине XVI в. считали эту траекторию состоящей из прямолинейных
отрезков и дуг окружности. Первые соображения об определении формы этой
траектории путем сложения равномерного горизонтального и неравномерного
вертикального движения ядра были высказаны Карданом (1501 – 1576). Но только
Галилей показал, что тело, брошенное в пустоте под некоторым углом к горизонту,
будет двигаться по параболе, представляющей собой горизонтальное движение с
постоянной скоростью и вертикальное падение с постоянным ускорением. Использованная
здесь идея сложения горизонтального и вертикального движений была развита
Галилеем в общий закон независимости действия сил, согласно которому появление
новой силы, не изменяет действие ранее приложенных сил. Обобщение именно этой
задачи облегчило разработку Ньютоном закона всемирного тяготения, согласно
которому все тела притягиваются друг к другу с силой обратно пропорциональной
квадрату расстояния между ними. Справедливости ради, необходимо сказать, что до
опубликования Ньютоном этого закона, мысль о его существовании высказал в
письме к Ньютону Р. Гук (1635 – 1703). Это послужило в дальнейшем предметом
многолетних дискуссий о приоритете этого закона. Дальнейшие исследования
творчества Ньютона, в том числе и анализ рукописей, опубликованных после его
смерти, показал, что закон всемирного тяготения был известен Ньютону и до
письма Гука. Более подробно с этим можно познакомиться, прочитав, например,
брошюру В.И. Арнольда, см. [25]. Если бросать ядро горизонтально с какой-нибудь
высоты, то по мере увеличения начальной горизонтальной скорости бросания, ядро
будет падать все дальше и дальше и при определенной скорости превратится, как
сейчас говорят, в спутник Земли. Существует предание, что как-то раз, во время
чумы 1665 –1666 гг., молодой Ньютон в
тиши своего садика в Вулсторпе вдруг обратил внимание на падающее яблоко и
глубоко задумался. Если яблоко падает на землю, т.е. Земля притягивает его, то
и Луна тоже должна притягиваться Землей, – падать на нее. Но «упасть» на Землю
Луна не может, поскольку имеет определенную горизонтальную, точнее говоря –
тангенциальную, скорость, как это имеет место в случае с ядром. Аналогичная ситуация
справедлива и для пар Солнце - Земля (и других пар планет солнечной системы).
Можно сказать, что в основе механики Ньютона лежат обобщения на любые, том
числе и космические тела, результатов Галилея, который не выходил за рамки
земного. Такое обобщение не было тривиальным и требовало не дюжего ума и
таланта, которым в полной мере обладал Ньютон. Тем самым Ньютон придал всеобщий
характер этим законам, и таким образом построил единую механику для небесных и
земных тел.
Распространяя
эти положения (в частности, закон инерции и свой второй закон о том, что сила
пропорциональна ускорению) на любые тела, Ньютон вынужден был ввести в
рассмотрение универсальное абсолютное пространство, которое по определению
всегда и всюду одинаково и абсолютно неподвижно. Далее, Ньютон ввел и «абсолютное, истинное математическое время»,
которое «само по себе и по своей
сущности, безотносительно к чему-либо внешнему, протекает равномерно и иначе
называется длительностью». Необходимо сказать, что время – это наиболее
широко и часто используемое понятие не только в физике, но и в повседневной
жизни. Вместе с тем, это и наименее полно осмысливаемое понятие. «Я прекрасно знаю, что такое время, пока не
думаю об этом. Но стоит задуматься, – и вот я уже не знаю, что такое время».
Эти слова, сказанные много веков
назад Блаженным Августином (357 – 430),
философом, много размышлявшим о восприятии времени, ни в чем не потеряли своей
актуальности до сих пор и полностью могут быть отнесены и к понятию
пространства. Ньютону понадобилось различать понятия гравитационной массы,
входящей в закон всемирного тяготения, и инерционной массы, являющейся коэффициентом
пропорциональности между силой и ускорением. Численное равенство значений этих
масс, полученных экспериментально Ньютоном, а ранее Галилеем, позволяло пользоваться единым понятием
массы. В настоящее время равенство гравитационной и инерционной масс,
экспериментально прослеживается с точностью – до 10-12 , и оно лежит
в основе общей теории относительности Эйнштейна. Согласно теории Ньютона
притяжение тел осуществляется в пустом пространстве при любом удалении их и
происходит мгновенно – вне времени, без непосредственного контакта тел – так
называемое дальнодействие. Свойство притягиваться друг к другу, заключено в
самих телах.
Теория
гравитации Ньютона вызвала резкое неприятие ее, и суровое осуждение со стороны
фактически всех ученых конца XVII – начала XVIII вв. Х. Гюйгенс (1629 – 1695) находил Ньютонов «принцип тяготения» нелепым и выражал
свое удивление тем, как Ньютон мог потратить столько сил на трудные вычисления,
основанные на таком принципе. Г. Лейбниц (1646 – 1716) выражал уверенность в
том, что нельзя удовлетвориться «притягательным
свойством, как это видимо, делает Г-н Ньютон». Лейбниц считал: «Тело естественным образом не может быть
приведено в движение иначе, чем посредством другого тела, прикасающегося к нему
и таким образом вынуждающего его к движению, и после этого оно продолжает свое
движение до тех пор, пока соприкосновение с другим телом не воспрепятствует
этому. Всякое другое воздействие на тело должно быть рассматриваемо как чудо
или чистое воображение». К этим мнениям присоединились братья и И. Бернулли
и Я. Бернулли (1667 –1748; 1654 – 1705). Такое единодушное осуждение теории
Ньютона объясняется, по-видимому, тем, что ранее аналогичные попытки уже были
осуждены, и к тому времени господствовали совершенно другие взгляды. Фонте Нель
(1657 – 1757) писал в «Похвальном слове Ньютону»: «Тяготение и Пустота, изгнанные Декартом из физики, казалось бы,
навсегда, ведомые Ньютоном, вернулись туда, быть может, только в несколько ином
виде, да еще с такой совершенно новой силой, на которую их считали способной».
Представляет интерес, с какой резкостью Декарт нападал на Роберваля (1602 -
1675), вводившего еще до Ньютона всемирное тяготение (без явного выражения для
закона его действия) в свою систему мира: «Нет
ничего более абсурдного: …автор предполагает, что некоторое свойство присуще
каждой частице материи в мире и что, в силу этого свойства, частицы
устремляются друг к другу и взаимно притягиваются; он предполагает также, что
подобное свойство присуще всем земным частицам в их взаимоотношениях и что оно
отнюдь не мешает первому. Чтобы это понять надо - не только предположить, что
каждая частица материи одушевлена, но даже и то, что в ней имеется большое
число различных душ, друг друга не стесняющих, но и то, что эти души
материальных частичек одарены сознанием и что они воистину божественны, дабы
они могли без всякого посредства знать, что происходит в весьма удаленных от
них местах, и оказывать там свое действие».
Таким
образом, можно констатировать, что после опубликования Ньютоном этих своих
работ началась многовековая дискуссия о том, передаются ли взаимодействия между
телами на расстоянии без посредства чего-нибудь (дальнодействие), или для
передачи взаимодействия необходим какой-нибудь посредник, в частности, - среда,
так что взаимодействие передается последовательно от одной точки среды к
соседней точке (близкодействие). Интересно, что самого Ньютона трудно отнести к
сторонникам одной из этих противоположных точек зрения, учитывая, что ему
принадлежит следующее высказывание, содержащееся в его третьем письме к Бентли:
«Нельзя представить себе, каким образом
грубое неодушевленное вещество могло бы без посредства чего-либо постороннего,
которое не материально, действовать на другое вещество иначе как при взаимном
соприкосновении. А так должно было быть, если бы тяготение было, в смысле
Эпикура, присуще материи. Вот почему я желал бы, чтобы вы не приписывали мне
учение о тяжести, прирожденной материи. Допустить, что тяготение урожденно
материи, присуще ей, так что одно тело должно действовать на расстоянии через
пустоту на другое тело без посредства чего-либо постороннего, с помощью
которого действие и сила от одного тела проводится к другому, есть для меня
такая нелепость, что, полагаю, в нее не впадет ни один человек, способный к
мышлению о философских вещах. Тяготение должно вызываться некоторым фактором,
действующим согласно определенным законам». Здесь эту цитату обычно обрывают,
хотя принципиально интересно ее следующее продолжение: «Каков этот фактор, материальный или не материальный, - я представляю
размышлению моих читателей». Но если этот фактор не материальный, то
читателю не остается другого выбора, как допустить божественное участие в
тяготении, что отнюдь не украшает научную теорию.
Существует
мнение, что концепцию дальнодействия ввел в физику ученик Ньютона кембриджский
математик Котс в предисловии ко второму изданию «Начал» Ньютона в 1713 г.
Предполагают, что это предисловие Ньютон перед изданием не читал, во всяком
случае, отсутствуют его высказывания о согласии или не согласии с этим
предисловием. Но, так или иначе, не смотря на возражения многих ученых, к ним
можно отнести и ученых следующих поколений, – таких как М. Фарадей (1791 –1867),
Д. Максвелл (1831 – 1879), В. Томсон (1824 – 1907), Э. Мах (1838 –1916) и др. -
эта концепция господствовала до XIX
столетия. Концепцией дальнодействия
описывались даже первые теории электрических взаимодействий. Конец этому господству
положила теория электромагнитного поля Максвелла, основанная на концепции
близкодействия. С тех пор, последняя концепция - в виде современной теории поля
- можно сказать, доминирует, и по сей день. Вместе с тем, не потеряла своей
актуальности и концепция дальнодействия, в рамках которой можно, как сейчас
понятно, описать как теорию электромагнитных, так и теорию гравитационных
взаимодействий. Эти теории, ничем не уступающие общепринятым теориям Максвелла
и Эйнштейна, сейчас известны под названием теории прямого меж частичного
взаимодействия. Согласно концепции прямого меж частичного взаимодействия из теории исключается понятие поля как
таковое. Частицы взаимодействуют друг с другом непосредственно «на расстоянии». При этом пришлось
ввести ряд дополнительных определений в формулировке принципа действия, суть
которых сводилась к тому, что нужно было учесть не только парные взаимодействия
между частицами, но и тройные, четверные и т.д. В настоящее время эта и многие
другие подобные теории находятся в стадии развития, а некоторые из них
отвергнуты. Более подробное обсуждение такого рода работ не входит в цели
настоящей брошюры. Как будет развиваться противостояние двух противоположных
концепций взаимодействия – дальнодействия и близкодействия, покажет будущее.
Ниже сделана попытка, конспективно изложить идеи построения физики вообще без
использования понятия взаимодействие, как его понимают сторонники обоих
подходов – дальнодействия и близкодействия. Предлагаемый подход представляется
перспективным, т.к. позволяет не только снять противоречия между этими
концепциями, но и существенно упростить физику и наметить пути решения основной
проблемы ее – создание Единой Теории физики. Заметим, что принципиальным является
уже сам факт упрощения физики, поскольку известно, что истина всегда проста. В
частности, известный физик из Техаса Джон Уилер говорил, что, открыв
окончательные физические законы, мы будем поражены тем, что они не были очевидны
нам с самого начала.
Глава 2.
Попытка философского осмысливания естествознания
Изложенное
в этой главе не претендует на роль даже конспективного изложения такого
глобального вопроса как философское осмысливание естествознания, имея ввиду,
что под философией ниже понимается наука
о наиболее общих законах развития природы, общества и мышления. Автор,
не являясь специалистом в области философии, не вправе даже хотя бы кратко
касаться истории этого вопроса, не говоря уже об обсуждении тех или иных
направлений в философии, имеющих место в этой проблеме. Более того, будучи естественником,
автор с симпатией относится к следующему высказыванию И. Ньютона: «Философия – это такая наглая и сутяжная
леди, что иметь с ней дело – это все равно, что быть вовлеченным в судебную
тяжбу…». Само собой разумеется, что сказанное отнюдь не отрицает важность и
даже необходимость философии в осмысливании естествознания. Связано это не
только с тем, что философия едва ли не старше естествознания (если только
допустимо разделять их), а и с тем, что во многих случаях философия помогает
естествознанию «не сбиться с пути истинного». Любой, кто рискнет затронуть
фундаментальные вопросы естествознания, с неизбежностью вынужден будет
затронуть и соответствующие философские проблемы. Это имело место в отношении
всех упомянутых в предыдущей главе ученых, включая и автора выше приведенного
высказывания. Известно, что сам Ньютон и все современники считали его
специалистом в области «натуральной философии». Таким образом, поскольку ниже сделана
попытка предложить нетрадиционный подход к физике, то придется коснуться некоторых
основных философских вопросов и сформулировать отношение к ним.
До
сих пор общепризнанно считать физику сугубо эмпирической (экспериментальной)
наукой, т.е. наукой, построенной на эмпириях – непосредственных опытных данных
(чувственных восприятиях). В определенном смысле противоположностью
эмпирическому подходу является так называемое аксиоматическое построение науки,
типичным представителем которой является геометрия, да и вся математика.
Понятно, что аксиоматическое построение любой науки более предпочтительно, т.к.
позволяет обходиться наименьшим числом самых простых и очевидных положений –
аксиом, и при этом получать наиболее общие результаты, при минимальных
материальных, временных и др. затратах. Ниже сделана попытка, показать, что
физику не только можно, но и целесообразно строить аксиоматически, поскольку
при этом удается решить некоторые фундаментальные проблемы естествознания и
существенно упростить физику, что само по себе немало важно. Принципиальное
отличие ниже изложенного от традиционной физики заключается уже в том, что,
начиная с самого начала, никоим образом не применяются традиционные понятия и
подходы к описанию физических явлений. Кстати, это и позволяет при чтении ниже
изложенного обходиться без глубокого знания таких подходов. В соответствующих
местах традиционные подходы конспективно изложены, но только лишь для того,
чтобы противопоставить им предлагаемые положения. Достаточно сказать, и об этом
уже говорилось во Введении, что при описании явлений природы не используются
следующие основополагающие понятия традиционной физики – метрическое пространство
и время (пространственно-временной континуум), система отсчета, силы или силовое
поле и др. Это вызвано лишь тем, что эти традиционные понятия вводятся на интуитивном
уровне, и их самостоятельное существование не может быть строго обосновано
экспериментальным путем как это имеет место для физических объектов. Вытекающая
отсюда недостаточная однозначность толкования этих понятий служит препятствием
для дальнейшего развития физики и всего естествознания, в частности, - для
создания Единой Теории Естествознания, иногда называемой Великим Объединением.
Здесь уместно напомнить бессмертное изречение Самюэля Батлера (1612 – 1680): «Я не осуждаю лжи, но я ненавижу неточность».
В связи с отказом от использования указанных исходных понятий традиционной
физики совершенно иначе осмысливаются и понятие взаимодействие физических
объектов, понятия их масс и понятие пространственной и временной удаленности их
друг от друга.
Как
это обычно имеет место при аксиоматических построениях, ниже в начале дается
определения того, что является предметом изучения физики, а также и
используемым в ней понятиям и терминам. Сразу же необходимо оговорить, что с
помощью бытового человеческого языка сделать это достаточно строго, и в полном
объеме крайне сложно. Связано это с тем, что сам такой язык нестрогий
(неоднозначен), и поэтому порядка на 50% переопределен. Когда необходима
строгость и однозначность, предпочитают пользоваться существенно более
подходящим языком, чем бытовой, например, единым у всего человечества языком
математики. А когда надо общаться не друг с другом, а с неживой природой,
например, с компьютером, то создаются специальные компьютерные языки. По
понятным соображениям, в том числе и с учетом высказанного во Введении
предполагаемого и не обязательно профессионального контингента читателей данной
брошюры, будем пользоваться ниже в основном бытовым человеческим языком, зная,
что при всей не строгости его люди благополучно общаются между собой и, рано или
поздно, приходят к взаимопониманию в любых сложных проблемах. Языком математики
воспользуемся лишь для упрощения (сокращения) рассуждений и для получения
некоторых специальных количественных результатов.
В
дальнейшем с единых позиций даются определения математических и физических
объектов, с которыми имеют дело соответственно математика и физика. В
частности, математика имеет дело в качестве исходных объектов с целостными (несоставными)
объектами или системами их, наделенными лишь каким-то одним качеством (для
разных объектов – различным), и не обладающими количеством такого качества.
Например, в геометрии различные точки, линии, поверхности и др. не могут иметь
различное количество своих качеств, т.е. не могут быть более
«правильными/истинными» чем другие такие же объекты. В то время как физика
изучает составные объекты и их системы, обладающие не только различными качествами,
но и количествами соответствующих качеств. Исходя из ниже приятых определений, показывается
возможность построения физики в рамках аксиоматического подхода, при котором
можно описать поведение физических объектов в строгом соответствии с фактически
реализуемыми способами наблюдения за ними. Это позволяет не только существенно
упростить физику, что само по себе является немало важным, но и появляется,
возможность решения таких фундаментальных проблем физики как проблема
необратимости во времени наблюдаемых физических явлений. Появляется возможность
осмысливать и описывать любые физические объекты с единых позиций, а не дифференцировать
их в зависимости от способностей испытывать гравитационные, электромагнитные,
сильные, слабые и возможно другие взаимодействия. В качестве универсальных элементарных
изменений, с помощью которых возможно наблюдение за поведением физических
объектов, приняты следующие, наиболее надежно фиксируемые и осознаваемые
события (акта). Им являются изменения (увеличение или уменьшение) на единицу количества
наблюдаемых объектов системы. Для краткости, эти события будем назвать соответственно
«рождение» или «излучение» и «смерть» или «поглощение» объекта. Показано, что математика и физика имеют не
только единую идеологию – парадигму, основанную на понятии «предшествования»
(эквивалентному понятию «больше/меньше»), но и единую методологию построения.
При этом математика может рассматриваться как частный (предельный) случай
физики, соответствующий бесконечной величине предшествования «рождения» и «смерти»
специального объекта, называемого сигналом. Для физики такая величина
предшествования, определяющая скорость движения самого сигнала и любых изменений
физических объектов, конечна.
1. Принципы определения используемых понятий
Чтобы уменьшить риск того, что рассуждения при
нетрадиционном построении физики могут явиться схоластическими и бесплодными, а
тема этих рассуждений отнюдь не затрудняет такую опасность, необходимо начать с
дефиниций/определений используемых ниже понятий и терминов, о чем уже
говорилось выше. Это тем более важно,
поскольку исходные и широко применяемые традиционной физикой понятия далее, как правило, не используются. Следует заметить, что
всякое определение фактически содержит в себе и аксиому, так как, определяя,
скрыто утверждают существование того, что определяют, а также и наличие у него
соответствующих свойств. Можно сказать, что имеет место и обратное положение.
По авторитетному мнению А. Пуанкаре см. [12], стр.41 «..аксиомы
геометрии (я не говорю об аксиомах
арифметики) суть не более чем замаскированные определения». Таким образом, при изложении нетрадиционных
представлений возможны уточнения и изменения терминологической базы традиционной
физики, т.е. не исключена возможность и необходимость иного осмысливания
существующих или даже введения новых терминов или понятий. Разумнее всего
представляется руководствоваться следующим положением, высказанным Рене
Декартом: «Всякий раз, когда я хочу
ввести новый специальный термин, я выбираю его из слов, находящихся в
употреблении, и то из них, которое мне кажется подходящим, я всегда употребляю
в установленном мною значении». Аналогичные
высказывания имеются и у других авторитетных ученых, например, у В.
Гейзенберга, см. [2] стр. 26: «Понятия
классической физики являются уточненными понятиями нашей повсеместной жизни и
образуют важнейшую часть языка, являющегося предпосылкой всего естествознания.
Наше действительное положение в естествознании таково, что для описания
эксперимента мы фактически используем или должны использовать классические
понятия. Иначе мы не поймем друг друга». Желание и потребность формализовать используемые
при рассуждениях понятия существует, образно говоря, со времен «Адама и Евы», и
преследует не только философские цели, но и сугубо прагматические (в конечном
итоге, такие же цели преследует и сама философия). Потребность более строгой
формализации стала особенно очевидной в связи с существенным прогрессом,
достигнутым в последнее время в естествознании, в частности в физике после
создания теорий относительности и квантовой механики. Имеются в виду возникшие
с новой силой (строго говоря, они никогда не прекращались с библейских времен)
дискуссии о том, можно ли построить Единую Теорию Естествознания. Допустимо ли,
признавать существование чего-то независимо от возможности наблюдения его? Что
такое наблюдение и какова степень познаваемости природы? Детерминированы или
вероятностны законы такой познаваемости, и что следует понимать под последними
терминами и т.п.? Ниже изложены нетрадиционные подходы к физике, позволяющие,
как представляется, глубже вникнуть о суть этих проблем. Благодаря этому
открывается, возможность существенно продвинуться в естествознании и тем самым
достигнуть дальнейшего прогресса в развитии технологий, что является весьма
важным для повсеместной жизни.
Сразу
же укажем, что использование термина «наблюдение» не предполагает
принципиальную несовместимость, и уж тем более антагонизм, следующих двух
понятий: того, кто наблюдает, и того, что наблюдается. Т.е. не предполагается,
что субъект и объект (человек и природа) два не связанные и независимые друг от
друга понятия. Человек мыслится лишь как часть природы, а часть не может
существовать и осмысливаться без целого, как и целое немыслимо в полном объеме без
всех своих частей. Поэтому человечество и природа не могут быть независимыми
друг от друга. С учетом этого, сформулированный выше вопрос о том, допустимо ли
признавать существования чего-то независимо от возможности наблюдения его, в
практическом плане является схоластическим (бесплодным) и лишенным смысла.
Любой ответ на этот вопрос – положительный или отрицательный – не возможно экспериментально
ни подтвердить, ни опровергнуть. Разумнее всего считать, что поскольку человек
– это и есть сама природа (ее часть), то и плоды его деятельности, в частности,
возможность наблюдать, бессмысленно отделять от природы и формулировать такие
вопросы. Ничем другим, кроме амбициозных соображений, основанных на том, что
только человечество может обмениваться информацией внутри себя, нельзя
объяснить (оставаясь в рамках естествознания) отношение к человеку, как к
чему-то, принципиально отличающемуся от любой другой части природы, например, от
системы «неживых» объектов. И мало кому приходит в голову обсуждать вопрос о
допустимости для одного такого объекта «признавать или не признавать»
существование другого объекта или его части, в зависимости от возможностей
«наблюдения» их друг другом и обмена между ними информацией. Вопрос об объективности
и субъективности наблюдения (познания) чего-либо более подробно обсуждается
ниже.
Ключевой
проблемой, с которой начинается физика (можно сказать, начинается
естествознание), и которая до сих пор полностью не решена, является проблема
движения, или в общем случае, – проблема изменения. Эта проблема не только
физики, но других сторон человеческого бытия, т.к. она затрагивает широкий круг
вопросов, включая философию, и даже религию. Понятие движение/изменение,
кажущееся, на первый взгляд, очевидным, на самом деле таит в себе много
неопределенного, воспринимаемого разными людьми и даже научными школами
по-разному. В частности, нет единства в понимании того, является ли
движение/изменения абсолютными или всегда только относительными. Объективны ли
изменения или зависят от способов наблюдения за ними субъектов. Осуществляются
ли движения/изменения всегда естественным образом или обязательно имеются
причины возникновения или прекращения их. Дано ли нам – «простым смертным»,
познать эти причины, и если да, то до какой степени. Или «Великий Создатель»
разрешил асимптотически приближаться лишь к тому «как» происходит движение,
оставив за собой право, знать – «почему» оно имеет место. А может быть даже и
ему не дано это право и все определяет «Его Величество Случай». Можно
констатировать лишь одно – «Создатель» не счел нужным посвятить нас в свои
замыслы, но он наделил нас разумом с тем, чтобы мы были в состоянии
последовательно раскрывать его планы, даже не будучи уверенными, в том, что нам
удастся это сделать в полном объеме.
Вся
история естествознания – это история попыток сформулировать логически
непротиворечивые друг другу и экспериментально наблюдаемым явлениям ответы на
выше сформулированные и другие аналогичные вопросы. На разных этапах этой
истории ответы на указанные вопросы были диаметрально противоположны. Известно,
что в ХХ веке произошли наиболее радикальные трансформации в представлениях о
природе, в результате чего естествознание лишилось твердого материального
фундамента, на котором оно находилось прежде. Это явилось следствием разработки
двух теорий – теории относительности и квантовой механики. «Можно сказать, что современная атомная физика столкнула естествознание
с материалистического пути, на котором оно стояло в XIX веке» см. [2]
стр. 28. Это авторитетное мнение выдающегося физика-теоретика, одного из
создателей квантовой механики, Вернера Гейзенберга (1901 – 1976). Согласно
современным представлениям основу нашего мира составляет не материя, а энергия.
Некоторые считают, что это одно и тоже понятие, но тогда не оправдано
присваивание им разных имен. «Фактически
энергия это то, из чего созданы все элементарные частицы, все атомы, а потому и
все вещи. Одновременно энергия является движущим началом… Энергия есть
субстанция… Энергия может превращаться в движение, в теплоту, в свет и
электрическое напряжение. Энергию можно считать первопричиной всех изменений в
мире», см. [2] стр. 31. Эта принадлежащая тому же В. Гейзенбергу попытка определить
энергию как нечто всеобщее, более откровенно и доходчиво прокомментирована (в
не связи с этой цитатой) в широко известных «Фейнмановских Лекциях по Физике»,
по которым обучаются студенты США и других стран. «Важно понимать, что физике сегодняшнего дня неизвестно, что такое
энергия», см. [3] стр.74. Аналогичного мнения придерживался и А. Пуанкаре,
см. [12], стр. 87: «В каждом частном
случае мы ясно видим, что такое энергия, и можем определить ее – по крайней
мере, предварительно; но найти общее определение ее невозможно. Как только мы
хотим выразить принцип во всей его общности и приложить его к Вселенной, мы
видим, что он, так сказать, испаряется и от него остается только следующее:
существует нечто, что остается постоянным». Напомним, что и теории
относительности и квантовая механика созданы в первой половине ХХ века – точнее
в первой четверти его (теории
относительности созданы в 1905 и 1916 гг., а квантовая теория в основном была
завершена к 1925 г.). Весь ХХ век прошел в попытках, в том числе и со стороны
авторов этих теорий, создать фундаментальную Единую Теорию. Причина того,
почему эти попытки окончились неудачно, заключается отнюдь не в отсутствии
достаточной квалификации ученых. Такой квалификацией (и фантазией, весьма
необходимой для занятия естественной наукой) ученые ХХ века обладали и, можно
даже сказать, в чрезмерных количествах. По этому поводу даже существует одна из
наиболее популярных среди физиков шуток, в которых, как известно, содержится
лишь доля шутки, а остальное … правда: «Ни одна физическая теория не может быть
правильной, если она не достаточно сумасшедшая/фантастическая». Причина упомянутых
неудач лежит гораздо глубже и вызвана чрезмерным консерватизмом традиционной
физики, который проявляется в желании полностью сохранить идеологию и методы
аналитического описания явлений природы, принятые еще во времена Галилея и
Ньютона (и даже раньше) при становлении современной физики. Об этом подробнее
говориться далее.
Вклад
в дематериализацию физики внесли как теории относительности (специальная и общая),
так и квантовая механика. Существование этих различных теорий, описывающих одну
и ту же Природу, не может не вызвать чувство неудовлетворенности. И не только
потому, что (по утверждению ранее цитированного Гейзенберга)…«более точное исследование показало, что обе теории (квантовая и
теория относительности) вступают в определенном пункте в конфликт, в результате
чего и проистекают все дальнейшие трудности», см. [2] стр. 98. Обе теории
принципиально по-разному подходят к вопросам детерминизма (предсказуемости),
причинности, степени объективности или субъективности и полноты знаний.
Известны следующие наиболее эмоциональные высказывания по этому поводу Альберта
Эйнштейна. «Бог в кости не играет» и «Бог изощрен, но не злонамерен».
Претензии к квантовой теории высказывал не только Эйнштейн, стоявший у истоков
этой теории. Например, Макс Планк (1858 – 1947), впервые предложивший идею
квантов, тоже полностью не принял эту теорию, а один из авторов ее – Эрвин
Шредингер (1887 – 1961) в итоге пришел к выводу, что она не является
окончательной. Даже сам Поль Дирак (1902 - 1982), создатель релятивистской
квантовой механики, заявил: «Очень может
быть, что в новой квантовой механике будет присутствовать детерминизм, который
имел в виду Эйнштейн... Вполне вероятно, что он окажется прав». Эти
высказывания сохраняют свою актуальность и до сих пор.
Одной
из причин того, что физика периодически, и относительно часто, испытывает
необходимость фундаментальных изменений, является эмпирический подход к
построению физики, основанный только на чувственных восприятиях (эмпириях) и
умаляющий значение логического анализа и теоретических обобщений. Иллюстрацией
таких фундаментальных изменений является вся предыдущая история развития
физики, кратко изложенная в главе 2, а также современные тенденции, о которых
будет идти речь ниже. При эмпирическом подходе, по мере появления новых
экспериментальных данных приходится не просто уточнять существующие
закономерности, а иногда приходится, и пересматривать философское обоснование
физики. В тоже время, аксиоматически построенная наука подобные фундаментальные
потрясения может испытывать только при изменении аксиом, что происходит, как
правило, существенно реже, чем уточнение (изменения) наблюдаемых опытных
данных. Примером может служить геометрия, кстати, делавшая, свои первые шаги тоже
как наука о наблюдаемых телах. Она строится аксиоматически на основании малого
числа аксиом – априори сформулированных исходных положений, в которых даже не
фигурируют понятия, имеющиеся в доказанных на
основании этих аксиом теоремах. При этом полученные в результате
доказательств соотношения между этими понятиями (свойства их) могут быть как
очевидными, так и совершенно не прогнозируемыми. Примером первого типа
соотношений является общеизвестное из опыта с самых древних времен и часто использующееся
в практике соотношение между катетами и гипотенузой прямоугольного треугольника,
носящее название теорема Пифагора. Не смотря на очевидность и общеизвестность
такого соотношения, оно существует в геометрии не как постулат, а как теорема -
теорема Пифагора (6 век д.н.э.). Но
возможно ли аксиоматическое построение такой сугубо экспериментальной науки как
физика? Ниже сделана попытка - показать, что это не только возможно, но и целесообразно.
Такое построение существенно упрощает физику, приводит к прогрессу в
осмысливании упомянутых ранее понятий движения и изменения, и тем самым,
приводит к решению фундаментальных проблем физики. Немало важно и то, что
удается заново осмыслить материальное начало всего естествоЗНАНИЯ, включая и
математику, а не только физику.
Следует
отметить, что стремление вывести все действия природы из «ясных и отчетливых идей» или первичных принципов (первопричин)
можно найти еще в «Principia philosophy» Рене Декарта.
Философский метод Декарта состоял в расчленении сложного восприятия на его
составляющие до тех пор, пока эти составляющие не сведутся к простым, ясным и
отчетливым идеям. Именно поэтому основной принцип своей философии он выразил
словами: «Cogito ergo sum» («Мыслю,
следовательно, существую»). Тем самым
истинность факта существования чего-либо, в том числе и самого себя,
связывается с возможностью осмысливания этого факта. Важным моментом при этом
было то, что Декарт не доверял никаким результатам и выводам предшественников,
коллег, учителей, если эти выводы не были в достаточной мере ясными и
интуитивно очевидными каждому. Он писал: «Я
заключил, что можно взять за общее правило следующее: всё, что мы представляем
себе вполне ясно и отчетливо, - все истинно…». И другого критерия истины, которая
должна быть «так тверда и верна, что
самые сумасбродные предположения скептиков не могут ее поколебать», для Декарта не существует. Представляется,
что этот принцип Декарта должен быть положен и в основу построения физики,
попытка чего и предпринята ниже. Имеется
в виду, принцип расчленения сложных понятий на более простые понятия до
такой степени, чтобы эти простые понятия «ясно
и отчетливо» воспринимались подавляющим большинством людей, а не только
незначительной группой специалистов. Как и искусство, наука, в частности,
физика не должны быть элитарными – понятными узкому слою общества. Это утверждение
созвучно ранее приведенным высказываниями В. Гейзенберга о необходимости
использовать такие физические понятия, которые позволили бы хотя бы большинству
людей (в идеальном варианте всем людям) понимать друг друга. В противном случае
физические теории недолговечны. Наиболее известными примерами, подтверждающими
сказанное, могут служить существовавшие раннее непродолжительное время теории,
построенные с использованием понятных только узкому кругу специалистов понятий,
таких как «теплород», «эфир», «физический объект с нулевой массой покоя» и
др. К сожалению, и сейчас многие фундаментальные
понятия традиционной физики являются элитарными, и неоднозначно осмысливаемыми даже
большинством специалистов. Интересную подборку высказываний по этому поводу
крупнейших физиков прошлого и настоящего можно найти, см. [23].
2. Дискретность
естествознания
Подчеркнем
следующее существенное положение, которое будем использовать в дальнейшем,
поскольку оно, по-видимому, является одной из фундаментальных особенностей
естествознания. Суть этого положения, ниже называемого дискретная особенность естествознания, заключается в том, что
однозначно определять и сравнивать между собой можно только такие понятия
(характеристики), которые допустимо осмысливать как конечные и единые целые или
как конечный набор таких целых. Можно сказать иначе, все однозначно
осмысливаемые понятия являются конечными. Приведенное положение принципиально
отличается от принятого традиционной физикой исходного положения о том, что
существование и любые изменения возможны только в, так называемом, априори
существующем безграничном (не имеющим ни внешних, ни внутренних границ)
пространстве и бесконечном времени – в пространственно-временном континууме.
Физику, основанную на этом положении, условно будем называть континуальной, в
отличие от дискретной физики, основанной на ниже изложенном подходе. Заметим, что применительно к математике
термины «дискретная» и «континуальная» являются широко распространенными, см.
[7]. Иногда дискретную математику отождествляют с дискретным анализом. Различие
между этими математиками, а также краткое современное осмысливание их, можно
найти, например, еще и в работе видного американского математика Г.
Биркоффа см. [5].
Можно
сказать, что из-за дискретной особенности естествознания понятие
пространственно-временного континуума в традиционной (континуальной) физике
однозначно определено быть не может, что является источником постоянных
дискуссий об основополагающих положениях естествознания. Как показано ниже,
осмысливание такого понятия как континуум практически не является необходимым
для описания природы. На основании данных нейрофизиологии и других наук все
большее число исследователей склоняется к тому, что любые чувственные
восприятия человека и животных (зрительные, слуховые, осязательные,
обонятельные и др.), а также любые события в природе, являются дискретными.
Другими словами, физические понятия обусловлены (или сами обуславливают) восприятием
имеющих место в природе простейших и наиболее надежно фиксируемых дискретных элементарных изменений, заключающихся в
увеличении или уменьшении чего-либо на какую-то конечную и единую часть.
Благодаря дискретной особенности естествознания существует понятие числа, с
помощью которого только и можно определять и сравнивать между собой любые
характеристики. Это имеет место как для детерминированных, так и для
недетерминированных – стохастических явлений, о которых речь пойдет ниже. В последних
случаях используются понятия, характеризуемые конечной числовой величиной
называемой вероятностью. С дискретной особенностью естествознания связано и то,
что скорость движения материальных тел конечна, и то, что для любых объектов и
явлений имеет место понятие предшествование их друг другу, и другие ниже
изложенные положения.
Как
свидетельствуют наблюдения за первобытными племенами (не имевшими еще контакта
с современной цивилизацией), за детьми, а также за животными, проще, и, прежде
всего, они осмысливают понятие количества (числа), а уж затем качества. Можно
даже сказать, что человечество как сообщество индивидуумов возникло и
продолжает существовать благодаря понятию чисел. Действительно, достоверно
известно, как об этом пишет известный американский математик М. Клайн см. [6]
стр. 49, что уже пифагорейцы (члены мистическо-религиозного ордена, существовавшего
в VI в. д. н.э.) «…усматривали
сущность вещей и явлений в числе и числовых соотношениях. Число для них было
первым принципом в описании природы, и оно считалось материей и формой мира. По
преданию, пифагорейцы полагали, что «все вещи суть числа»». Познать природу
(ее законы) можно только с помощью числа. При достаточно тщательном
рассмотрении, число лежит не только в основе науки, но и в основе искусства и
всего того, что можно осмыслить. «Пифагорейцам
принадлежит идея сведения музыкальных интервалов к простым соотношениям между
числами; они пришли к этой мысли, совершив два открытия. Первое это то, что
высота звука, издаваемого колеблющейся струной, зависит от ее длины. Второе, -
это то, что гармонические звучания издают струны, длины которых относятся между
собой, как целые числа». Достоверные сведения о более древних цивилизаций
Древнего Египта и Вавилона, около 3000 лет д. н.э., не сохранились, но
известно, что и у них были правила и формулы для оперирования с числами, и это
позволяло им решать практические задачи повседневной жизни.
Очередной
важной для нас особенностью естествознания является то, что в нем имеет место,
так называемый, «универсальный принцип
дуализма», на котором основана возможность познания законов природы, и даже
способ существования материи – способ жизни, заключающийся, в конечном счете, в
рождении нового и отмирания старого. Реализуется этот принцип благодаря
существованию для каждого понятия и явления «осевой симметрии» - двух
противоположных смысловых значений их, одно из которых может подтверждать, а
другое может отвергать соответствующее смысловое значение. Поэтому естественно,
что принцип дуализма является основой диалектики – метода познания явлений
действительности в их развитии и самодвижении, которое возможно в результате
«борьбы противоположностей». Ниже на этот принцип будем неоднократно ссылаться,
и использовать его. Подтверждением того, что этот принцип имеет место и
является универсальным, а правильнее говоря, проявлениями фундаментальности
этого принципа являются максимально долгие и проводящиеся в наиболее широком
диапазоне наблюдения за природой. Очевидно, что требованиям максимальной
полноты и длительности наблюдения за природой лучше всего отвечают языки
человеческого общения, т.к. они создавались (и продолжают совершенствоваться)
исходя из особенностей природы и для познания ее. А также, для обмена
информацией о таком познании между людьми одного и разных поколений, что
способствует сохранению естествознания и
существованию человечества как такового. Говоря иначе, наиболее достоверная
информация о структуре природы может быть накоплена именно языками общения.
Возможности познания всех фундаментальных закономерностей естествознания,
перечень которых еще далеко не полон, если он вообще когда-нибудь может стать
таковым, заложены неявным образом в языках, точнее говоря, в конструкции этих
языков, являющейся в определенном смысле и на каком-то уровне единой для всех
языков. Только благодаря такому единству и возможно общение людей, говорящих на
разных языках (перевод с одних языков на другие), и познание ими природы.
Принцип
дуализма в языках общения проявляется в том, что все эти языки допускают «возможность
отрицания» утверждений, только благодаря чему любое понятие или состояние и может
быть осмыслено с помощью другого альтернативного ему понятия имеющего противоположный
смысл путем сравнения и/или
сопоставления их друг другу. Примерами могут служить следующие понятия: активное,
ласковое, цветное, живое, одинаковое, теплое, постоянное, хаотическое и т.п. Вне
связи с альтернативными им понятиями сами эти понятия и состояния осмыслены
быть не могут. Именно этим вызвано существование любых таких понятий только в
виде пар, названия которых часто отличаются друг от друга лишь специальными
(отрицательными) частицами, являющимися обязательными атрибутами всех языков
общения. Знаки отрицания имеются и в едином у человечества и наиболее формализованном
математическом языке. Универсальность принципа дуализма и безграничные
возможности его стали еще более очевидными в связи с развитием цифровых
(компьютерных) технологий. В основе этих технологий лежит простейший дуалистический
принцип «да – нет» («возможно - невозможно»).
Используя его, современные технологии вплотную приблизились к уровню
развития, при котором отсутствует грань между искусственным и естественным
интеллектами. Впрочем, ничего удивительного в этом нет, т.к. нервные системы
любых живых существ работают на основе такого же такого же дуалистического
принципа. Заметим, что в рамках традиционного подхода к физике говорить об
универсальности принципа дуализма не приходится, поскольку в качестве исходного
понятия этой физики принято понятие пространственно-временного континуума, которое
не может быть однозначно осмыслено, из-за отсутствия своей дуалистической пары.
Если конечно не считать, что такое парой является полное отрицание
существование континуума как объективной реальности. Во многом этим объясняется
то, что до сих пор не удается на основе понятий континуальности удовлетворительным
образом построить физику, лишенную внутренних противоречий, и описывающую с
единых позиций все наблюдаемые физические явления.
4. Дуалистическая пара понятий:
объекты и субъекты
Исходя
из выше сформулированного и априори принятого «универсального принципа
дуализма», будем считать однозначно осмысленными (хотя бы в первом приближении,
- в дальнейшем осмысливание становится более точным) с помощью этого принципа,
следующие используемые в дальнейшем дуалистические пары понятий. Целое и часть;
количество и качество; больше и меньше; внутри и снаружи; искусственное и
естественное; объединение и разъединение; изменение и сохранение; порядок и
хаос и др. Качественное различие двух противоположных понятий каждой такой
дуалистической пары обусловлено только различием количественных значений
соответствующего качества (различием значений характеристик), и при изменении
этих значений противоположные понятия могут превращаться друг в друга, т.е.
изменять свое качество. В этом заключается суть закона перехода количества в качество, и наоборот. Поскольку
дуалистическая пара понятий «объект - субъект» являются наиболее важной и
наиболее часто используемой при осмысливании естествознания, попробуем формализовать
определение этих двух понятий.
Прежде
всего, заметим, что в соответствии с приведенным во Введении «основным
принципом теории познания» любое понятие надо соотносить с чем-то, что можно идентифицировать – однозначно отождествлять
с ним или отличать от того, что не является этим понятием. Как уже говорилось в
разделе о дискретности естествознания, это возможно только путем определения и
сравнения между собой численных значений характеристик, для чего это понятие
должно быть конечным. С учетом сказанного, под объектом будем понимать то,
что субъект может идентифицировать относительно других объектов, т.е. качественно
и количественно определять и сравнивать между собой их характеристики, с тем,
чтобы можно было однозначно отождествлять или различать объекты. Способы
получения и смысл таких характеристик будут указаны ниже. Понятие субъект можно
понимать как нечто противоположное объекту в смысле возможности идентификации
(если исходить из того, что эти два понятия являются дуалистической парой). Говоря
более точно – нечто противоположное в смысле возможности определять численные
значения всех характеристик субъекта. Поскольку такое определение субъекта не
конкретизирует это понятие, то более четким и поэтому более приемлемым
представляется следующее определение, эквивалентное предыдущему определению.
Под субъектом понимается то, что само
может идентифицировать, и что не может быть идентифицировано им в такой же степени,
объеме и такими же методами, как можно идентифицировать объекты, иначе субъект
был бы объектом. Достаточно сказать, что к субъектам не применим классический
(дуалистический) метод познания, который повсеместно применяется к объектам. Он
заключается в последовательном расчленение на более простые составные части, и
последующем, после анализа этих частей, объединение их в единое целое. Субъект
не может быть расчленен или разъят на части, поскольку в этом случае он
перестает быть субъектом. Субъект может существовать и осмысливаться только как
единое целое понятие, а не как система составляющих его частей. В этом смысле
говорят, что субъект является так называемым неразъемным «черным ящиком»,
достоверно познать устройство которого, не возможно из-за того, что его нельзя
разобрать на части, но относительно которого можно строить гипотезы (расчетные
схемы) и анализировать их с помощью его «входов» и «выходов». Строго говоря, даже
таким способом полное познание субъекта не может быть осуществлено за конечный
отрезок времени, что часто является одним из основных критериев субъекта.
Например, мы в состоянии отличить живого котенка от игрушечного, какой бы
совершенной внешне не была бы эта игрушка, исходя из того, что с течением
времени для нас поведение игрушки (объекта) будет полностью предсказуемо, а
поведение котенка (не говоря уже о поведении субъекта) нет.
Для
того чтобы подчеркнуть различие между понятиями объект и субъект, иногда
говорят, что объект принципиально способен познаваться сколь угодно полно, или
– потенциально детерминирован, а субъект – не способен даже в принципе
познаваться достаточно полно, или актуально недетерминирован (стохастичен).
Таким образом, объект и субъект могут, в какой-то мере характеризоваться своей
вероятностью (математической), под которой понимается «числовая характеристика степени возможности появления какого-либо определенного
события в тех или иных определенных, могущих повторяться неограниченное число
раз, условиях», см. [7]. Принято, что эта числовая характеристика может
принимать любые значения из диапазона ноль - единица. Поскольку в этом числовом
диапазоне столько же значений, как и в любом другом диапазоне (этот интервал
имеет мощность континуума), то вероятностью можно характеризовать любую, какую
только можно представить себе, «степень
возможности». Нулевое значение соответствует невозможности, а единица
соответствует обязательности наступления события при каждом повторении
указанных условий. Исходя из этого, события имеющие вероятности отличные от
нуля и единицы, называют случайными событиями, а события, имеющие вероятности ноль
или единица называют соответственно – невозможными и достоверными. К
приведенному определению вероятности необходимо добавить следующее замечание
выдающегося французского математика Э. Бореля (1871 – 1956): «..вероятность не существует отвлеченно, а только
по отношению к определенному человеческому мозгу, т.е. относительно некоторой
совокупности сведений», см. [8] стр. 13. Действительно, оценивать «степень возможности появления какого-либо
определенного события» может, как указано выше, только субъект. Отсюда следует,
с учетом введенных определений понятий субъект и объект, что вероятность
наступления какого-нибудь события можно понимать, как числовую характеристику «степени возможности» идентифицировать
конкретным субъектом, участвующие в этом событии объекты. Поскольку
идентифицировать физические объекты можно только опытным путем, то и
вероятность осуществления любого физического события субъект может определять
лишь путем экспериментов. Например, утверждать, что конкретный материальный
кубик является «абсолютно правильным» и выпадение каждой из шести граней этого
внешне симметричного кубика имеет одинаковую вероятность равную 1/6, можно
только после проведения достаточного числа испытаний его. Не существует иного
способа убедиться в «абсолютной правильности», т.е. полной симметрии реального материального
кубика – всех его характеристик - относительно трех взаимно перпендикулярных
плоскостей, проходящих через центр кубика. Кстати, только после введения в
наличный оборот единой европейской валюты выяснилось путем проведения
испытаний, что монеты «евро» не могут
использоваться для ведения абсолютно честной игры «орел/решка».
Таким
образом, понятия объект и субъект можно осмыслить только друг с помощью друга.
Вопрос о применимости закона перехода количества в качество к этой
дуалистической паре понятий, т.е. вопрос о том, могут ли, и если могут, то в
каких случаях, при каких условиях, в какой степени субъекты могут становиться
объектами или наоборот, требует особого рассмотрения, выходящего за рамки
рассматриваемого в данной брошюре. Заметим, что право быть субъектами люди
монополизировали себе, и это связано с тем, что не существует способа
однозначно убедиться в том, что «нечто», не являющееся человеком (не имеющее с
ним единого и достаточно развитого языка общения), может в достаточной мере
идентифицировать объекты. Хотя формально можно считать, что и животные, и
растения, и даже органические и неорганические вещества при химических
реакциях, тоже «создают свои знания» и используют их в своих целях. Например,
великий мыслитель и энциклопедист Дидро (1713 – 1784) провозглашал, что уже
сама материя должна быть чувственной, и даже камень обладает чувствительностью
в том смысле, что молекулы, из которых он состоит, активно ищут одни комбинации
взаиморасположения и избегают других, проявляя тем самым свои «симпатии» и «антипатии». При этом
чувствительность целого организма является просто суммой чувствительности его
частей. Не чужды аналогичным взглядам и некоторые современные теории квантовой
механики, в которых материя наделяется сознанием. Подробности и библиографию по
этому вопросу можно найти, например, в материалах продолжающейся на страницах авторитетного
журнала Российской академии наук дискуссии: «Квантовая механика: новые
эксперименты, новые приложения и новые формулировки старых вопросов», см. [9].
В художественной литературе известны приемы, когда объектам приписывают
свойства субъектов, например, наделяют детские игрушки или животных
возможностью общаться между собой и обсуждать поведение людей, хотя люди и не
слышат этого. Но это лишь аллегория. Заметим, что относительно недавно граница
между субъектами и объектами считалась
непреодолимой и совпадала с понятиями «живое» и «неживое» или с понятиями
«одушевленное» и «неодушевленное». В настоящее время различие между последними
понятиями с точки зрения физики (биофизики, молекулярной биологии, психологии,
нейрофизиологии и др.) достаточно размыто, и вследствие этого такие термины
стараются не связывать с понятиями субъект и объект.
Из
принятого выше определения понятий объект и субъект следует, что
фундаментальные законы природы могут формулироваться, или – что, то же самое, познаваться
только по мере необходимости и в рамках возможности реализовать это субъектами.
Другими словами, естествоЗНАНИЕ создается субъектами, исходя из своих
возможностей и по мере появления необходимости. Оно предназначено для
использования субъектами и ими оно может быть изменено. Подтверждением этому
является вся история развития естествознания, конспективно изложенная во 2-ой главе.
Подобные взгляды в прошлом высказывал Кант (1724 – 1804). Здесь не лишним будет
привести мнение одного из величайших физиков ХХ века А. Эйнштейна, высказанного
им (совместно с Л. Инфельдом) относительно используемых физических понятий. «Физические понятия суть свободные творения
человеческого разума и неоднозначно определены внешним миром, как это иногда
кажется», см. [10] стр. 30. Наиболее интенсивные попытки изменить даже такой
фундаментальный (как это представляется в настоящее время) закон природы как
закон гравитационного взаимодействия были предприняты во второй половине ХIХ и в первой половине ХХ вв., в связи с желанием
объяснить аномалию в поведении перигелия планеты Меркурия. Достаточно подробное
изложение содержания и хронология таких попыток приведены в прекрасной
монографии Н. Т. Роузвера, см. [6]. Ниже указано как, можно и целесообразно представить
механизм «гравитационного взаимодействия» иначе, чем это имеет место в
классической физике и в общей теории относительности, и, главное, более точно
описывать природные явления, основанные на таком представлении.
Следует
заметить, что отличать возможность от необходимости чего-либо для субъекта чаще
всего нельзя (обычно этого не может сделать даже сам субъект по отношению к
самому себе), как нельзя и определить, внутренними или внешними
обстоятельствами это обусловлено. В частности, нельзя определить, возможностью
или необходимостью обусловлена вера большого числа людей в судьбу, в загробную
жизнь и т.п., и связанная с этим вера в существование Бога. Т.е. нельзя определить,
кто или что является причиной такой веры, или веры гораздо большего числа людей
в существовании между физическими объектами «взаимодействия» в традиционном
понимании его, при котором предполагается наличие у каждого материального
объекта соответствующего свойства (собственной причины) «взаимодействовать». А
также определить существование каких-то носителей взаимных действий и механизмов
реализации их, например, действий материальных тел и планет друг на друга. Об
этом подробнее речь будет идти ниже. И вообще, нельзя определить, на чем основана
любая вера, которую следует отличать от знания, о чем подробнее говорится в
следующем разделе. Сколько-нибудь детальное обсуждение этого весьма сложного
вопроса не входит в цели данной брошюры, и поэтому ограничимся следующим
замечанием. По-видимому, существование любой веры обусловлено фундаментальным
(универсальным) принципом естествознания
- «принципом минимизации», в соответствии с которым вера во что-либо
требует меньших умственных и физических затрат по сравнению со знанием. Универсальность
этого принципа проявляется и в том, что минимизация имеет место, как это известно,
из традиционной физики, и для любых других событий, процессов и явлений
материального мира (имеются в виду вариационные принципы механики). Этим
принципом обусловлена и вера в существование Единой Теории Естествознания,
которая призвана минимизировать объем фундаментального знания и, следовательно,
затраты на получение его.
Под знанием обычно понимают то, в чем
субъект убеждается самостоятельно (без влияния другого субъекта), путем анализа
и осмысливания получаемых непосредственно им сенсорных (чувственных) восприятий.
Под верой понимают нечто противоположное,
а именно то, в чем субъект не может (не желает) убедиться только исходя из собственных
восприятий, но что он считает истиной (и тем самым отождествляет веру со
знанием) исходя из каких-то побуждений, являющихся мнением (знанием или верой)
других субъектов. В этом смысле говорят, что вера субъективна, и она может
изменяться, поскольку могут изменяться как побуждения соответствующих субъектов,
так и сами эти субъекты. Субъективной вере противопоставляют объективное
знание, основанное только на собственных восприятиях и осмысливании их, независимо
от каких-либо других субъектов. Такая объективность знания не спасает от
возможности изменения его и в этом отношении знание мало, чем отличается от
веры. Действительно, по мере развития и усложнения технологий, а также по мере
увеличения объема информации о природе всё труднее субъекту основывать свои
знания исходя из непосредственных сенсорных восприятий, и приходится полагаться
в этом вопросе на других субъектов. Понятно, что при этом увеличивается число
людей, отождествляющих веру со знанием (с естествознанием). Это имеет место,
например, в случаях отсутствия возможности убедиться в чем-то непосредственно
из-за технических сложностей или из-за того, что какие-то события произошли или
смогут произойти в месте, где субъект не мог или не сможет находиться. В этих
случаях то, что считается объективным знанием, всё в большей и большей степени
становится субъективной верой, основанной на мнениях других субъектов. При этом
также и знание об одном и том же, может трансформироваться, как и вера, вплоть
до противоположных значений. Это связано также и с тем, что абсолютно
объективными и не способными в дальнейшем измениться могут быть лишь уже
зафиксированные нашими органами чувств сенсорные восприятия. Но анализ
(осмысливание) такого восприятия, т.е. то что, получается в результате такого
анализа, и что мы, в конечном счете, называем «знанием», может быть различным у
разных людей, и даже у одного и того же
человека в разные периоды его жизни. Возможно также и неосознанное влияние на
такой анализ других субъектов. Как уже говорилось, человек является «черным
ящиком», и существующая в нем «программа обработки и анализа информации» не
может быть познана - она не является детерминированной. Т.е. строго говоря,
знание не является абсолютно объективным и неизменяемым, о чем уже говорилось
ранее и о чем свидетельствует весь ход развития естествознания. То, что
понимается под объективностью естествознания (независимостью его от отдельного
субъекта или от группы их), на самом деле является лишь констатация того, что
положения естествознания признаются большинством (правильнее сказать –
подавляющим большинством) всех субъектов. Неприятие отдельными субъектами
некоторых положений такого естествознания, принятых большинством, до поры до
времени игнорируется. Но именно такие отдельные личности, как правило, являются
двигателями прогресса, если им удается убедить большинство субъектов (иногда и
после своей смерти как, например, в случае с Джордано Бруно) в необходимости
внести соответствующие изменения в естествознание.
На
основании выше принятых определений объекта и субъекта, уже здесь – до
изложения нетрадиционного подхода, можно
сделать вывод о том, что все законы естествознания, не только уже познанные, но
и те которые предстоит познать, не могут стать даже в дальнейшем окончательными
и полными. Другими словами, никакие законы естествознания априори не
предопределены заранее и «до конца», в том смысле, что они не зависят от людей
и человечеству остается только, раньше или позже («когда будет на то божья
воля»), познать их, например, «методом проб и ошибок». Причина этого отнюдь не
в том, что «в игре с нами Бог бросает кости» и заранее не знает что выпадет,
как образно характеризовал Эйнштейн некоторые положения квантовой механики.
Если придерживаться терминологии «игры с Богом», то, скорее всего, Бог играет с
нами не в кости, а в карты. И хотя Бог знает «расклад всех карт» имеющихся на
руках у всех участников «игры», но он не желает заранее («до начала игры») открывать их нам, чтобы не пропала интрига.
Впрочем, никаких запретов пытаться познавать «расклад карт» в процессе «игры»
Бог не накладывает. Невозможность априори узнать «расклад карт», если не
привлекать понятие Бог, обусловлена универсальным принципом дуализма и, в
частности, существованием объектов и субъектов. Для субъекта отсутствует
возможность познания «всего и вся» в полном объеме, потому что он сам не может
быть полностью идентифицирован. Как уже говорилось, субъект во многом непознаваем
(непредсказуем) – вероятностен (недетерминирован).
Будем
исходить из того, что дуалистическая пара «объект-субъект» является простейшим понятием,
т.е. не допускающим определения только через другие – более простые понятия. Как
уже говорилось выше - во Введении брошюры, простейшие понятия должны
существовать, т.к. в противном случае определение любых понятий и суждений было
бы бесконечным процессом и, следовательно, оно не имело бы смысла. При определении простейших понятий использование их же самих,
наряду с другими более сложными понятиями, например, такими как
«идентификация», является вынужденным – единственно возможным. Будем также
считать очевидным и то, что любое понятие или явление имеет смысл только, если
его соотносить с определенным объектом и субъектом, т.е. если их можно
идентифицировать относительно и с помощью иных объектов и субъектов. «Нечто»,
что нельзя идентифицировать, т.е. то, что не является ни объектом, ни субъектом,
не может и не должно быть предметом рассмотрения науки, вообще, и данной
брошюры, в частности. Это связано с тем, что отсутствуют критерии подтверждения
или опровержения любых выводов, в том числе и самого факта существование этого
«нечто». Правильнее сказать, что последнее утверждение имеет отношение лишь к определению
того, что понимается под наукой.
Именно в этом смысле говорят, что результатом науки является знание, а не вера.
Из сказанного не следует, что «нечто», что нельзя идентифицировать не может
быть предметом для рассмотрения в рамках какой-либо иной человеческой
деятельности, результатом которой не является знание. В частности, примерами
такого рассмотрения частично являются некоторые виды искусства, а также -
теология, эзотерические учения, и даже некоторые выше упомянутые направления
квантовой физики, в которых материи приписывается понятия сознание, о чем
упоминалось выше.
6. Математические и физические
объекты
Следует
различать два типа объектов: математические и физические, которые являются
предметами рассмотрения соответственно математики и физики. Эти объекты
принципиально отличаются друг от друга и требуют различных подходов для
идентификации их. Под элементарными/исходными математическими объектами будем понимать простейшие для
осмысливания объекты, идентификация которых осуществляется субъектом
относительно таких же математических объектов непосредственно, т.е. без помощи
чего-либо внешнего по отношению к себе и к объекту. Такие элементарные объекты
представляют собой нечто единое и неделимое целое. Перефразируя следующее
определение, данное гениальным Евклидом математической точке: «точкой называется то, что не имеет частей»,
можно сказать, что элементарный математический объект это то, что не имеет количества,
а имеет только качество. Понятие количество применимо лишь к совокупности этих
объектов. Математика в своей основе как раз и занимается изучением в конечном
итоге количественных соотношений различных совокупностей таких (лишенных
количества) объектов, обладающих одним общим для них качеством (свойством). Для
подобной совокупности объектов называемых элементами, в математике введен Г.
Кантором (1845 -1918) специальный термин – множество. «Под множеством мы понимаем соединение в единое целое определенных
хорошо различимых предметов нашего созерцания или мышления», см. [13] .
Примерами математических множеств могут служить: совокупности точек евклидова
пространства, совокупности непрерывных в заданной области функций, и т.п. Для
содержательного развития теории множеств существенны лишь определенные
соотношения между элементами множества или между самими множествами, а не их
происхождение и связь с чем-либо другим. При этом находится значение
меры/расстояния между двумя элементами множества, количественно характеризующее
соответствующе единственное качество системы таких элементов. Эта
количественная характеристика не способна меняться естественным образом (без
участия внешнего фактора), если только не меняется само множество, поскольку у
элементов такого математического множества отсутствует какое-либо другое свойство
(качество), относительно которого возможны изменения. Можно сказать, что для
математического множества не имеет место закон перехода количество в качество,
т.к. сами элементы этого множества не имеют количества.
Под физическими объектами/явлениями будем
понимать объекты, в определенном смысле противоположные математическим объектам
в отношении способов их идентификации, т.е. такие объекты, которые субъект может
идентифицировать (или, как предпочитают говорить физики, наблюдать) каждый раз лишь
относительно конкретных физических (наблюдаемых) объектов и лишь посредством
других физических объектов. Это позволяет наделять физические объекты не только
качеством, как это имеет место для математических объектов, но и количеством
каждого качества. Такое определение физических объектов, кажущееся на первый
взгляд слишком субъективным, представляется все же наиболее приемлемым по
сравнению с другими традиционными и тоже еще более субъективными определениями.
Меньшая субъективность принимаемого определения обусловлена тем, что в
традиционных определениях физических объектов используются такие искусственно
введенные и еще более субъективные и максимально интуитивные понятия, как
пространство, время (пространственно-временной континуум), системы отсчета,
сила и другие интуитивные понятия. Эти понятия не являются самостоятельными,
т.е. их невозможно строго определить без использования понятия физические объекты
и поэтому трудно осмыслить. Именно в силу этого, эти вспомогательные понятия традиционной
физики ниже не используются. Принятое определение физических объектов означает,
что бессмысленно рассмотрение только одного такого объекта, и даже только двух объектов,
как это допустимо для математических объектов, т.е. не существует так
называемая «задача одного тела». Заметим, что в традиционной физике (механике)
последняя задача существует и, можно сказать, она является основной целью
физики. Суть этой задачи в том, чтобы определить поведение физического объекта
в «пространственно-временном континууме» под влиянием приложенных к нему заданных
действий/сил. То, что происхождение таких сил обычно пытаются как-то связывать
с другими массами, не меняет сути сказанного. В «задаче одного тела»
непосредственно рассматривается только
один объект, и его поведение не связано с поведением или даже с существованием
других объектов.
Таким
образом, принятыми выше определениями математических и физических объектов
помимо существования постулируется еще и принципиальная возможность счета их, как
говорят математики, – совокупность объектов является счетной. Также
постулируется и существование математических объектов в количестве не менее
двух, а физических объектов – не менее трех. Первый объект это идентифицируемый
объект, второй объект это объект, относительно которого идентифицируется
первый, а третий физический объект это объект, с помощью которого осуществляется
идентификация первых двух физических объектов. Физический объект не может
обладать только качеством (т.е. обладать только одним свойством), как это имеет
место для математического объекта. Помимо какого-то качества каждый физический
объект имеет еще и количество этого качества. Можно сказать, что поскольку
физический объект имеет счетное число свойств, то он является составным – состоящим из ни менее
трех своих частей или объектов, позволяющих ему иметь/проявлять различные
свойства. Допустимо и обратное утверждение: поскольку физический объект
является составным, он имеет счетное число свойств. Изменение свойств отдельных
объектов, составляющих единый физический объект, может повлечь за собой и
изменение каких-то характеристик такой составной системы, т.е. свойств единого
объекта, и наоборот. С учетом этого, ниже, если это специально не оговорено,
будем считать, что понятия физический объект и система их (в количестве не
менее трех объектов) могут адекватно применяться для описания одного и того же
явления при необходимости акцентирования различных свойств этого явления. Для
физического объекта нет никаких оснований априори считать, что различные
свойства его не связаны друг с другом. Следовательно, нет оснований считать,
что для содержательного развития теории физических объектов достаточно
рассматривать только независимые друг от друга объекты или даже пары их
(независимые пары частей их), как это допустимо для математических объектов.
Другими словами, нельзя рассматривать физический объект как нечто полностью
автономное или даже как систему независящих друг от друга пар математических
объектов, в которой изменение количества и качества таких пар никогда не
приводит к изменению самого физического объекта. Также нет оснований, считать,
что изменения физического объекта относительно каких-либо других объектов возможны
лишь при наличии внешнего по отношению к нему искусственного действия, как это
необходимо для изменений математических объектов. Действительно, опыт
подтверждает, что изменения физического объекта могут происходить и естественным
образом - путем изменения друг относительно друга внутренних его частей, т.е.
вне связи с изменениями внешних объектов, как правило, достаточно удаленных от
него, чтобы не считаться внутренними.
Такие
автономные изменения составных физических объектов, например, изменения конфигурации
и других характеристик их, не зависящие от внешних влияний, могут иметь место, как для микро объектов,
так и для макро объектов. Примерами первых объектов являются молекулы, атомы и
другие микрочастицы способные меняться указанным образом, а примерами вторых
объектов являются галактики и звезды, рождение, развитие и смерть которых
достоверно наблюдаются в достаточном числе случаях и при этом практически не
выявлено по отношению к ним никаких внешних воздействий. Вопреки всему выше указанному,
в традиционной физике все же считается, что для изменения физического объекта
всегда необходимо действие на него чего-то внешнего по отношению к нему, обычно
связанного с другими физическими объектами, и такое действие их называют силой
или силовым полем (для краткости - просто полем). Заметим, что понятие «поле»,
которое воспринял и широко применял Максвелл, было введено Ульямом Томсоном - лордом
Кельвиным (1824 – 1907) в противоположность понятию дальнодействия. Для
описания взаимного влияния объектов друг на друга было введено понятие массы
объекта, которая количественно характеризует свойство объектов, отличающихся
только массами, по-разному изменять свое состояние (свое движение) при одинаковом
внешнем действии на них. При этом говорят, что объект обладает свойством
тяготения. Считается, что массой обладают все физические объекты - без исключения. Более того, в традиционной
физике массу приписывают не только таким объектам, но и многим другим понятиям,
например, излучению, полям, энергии и т.п. Кроме обладания тяготением друг к
другу массы наделяют еще и свойством, принципиально отличным от этого свойства
– количественно характеризовать способность материальных объектов сохранять
свое состояние в случае прекращения внешних действий. При этом говорят, что объект
обладает инерцией. Заметим, что до сих пор в традиционной физике нет однозначного
мнения о причинах существования инерции. Иногда связывают движение по инерции
не с отсутствием каких-либо внешних действий, поскольку наличие их исключает
такое движение, а с невозможностью экспериментально выявить и определить
гносеологию этих действий. При этом считают, что такие действия существуют и
даже ведутся дискуссии о материальном происхождении инерции. Э. Мах, например,
считал, что инерция объекта обязана всем другим объектам – всему остальному
веществу во Вселенной и, в частности,
наиболее удаленным «неподвижным» звездам. Подобные идеи Маха оказали
большое влияние на молодого Эйнштейна. Следует сказать, что в теологии любое
внешнее влияние на объекты и даже на субъекты связывают с нефизическим понятием
«божество» и тем самым избегают дальнейших проблем с физическим обоснованием
причин различных изменений.
С
целью описания двух выше указанных особенностей физических объектов,
традиционная физика различает два вида масс, соответственно – тяжелую и
инертную массы, но количественно эти массы считаются одинаковыми между собой. В
силу того, что массой наделяют все физические объекты, считается, что они не
только действуют, но и испытывают в свою очередь действие друг от друга – так
называемые гравитационные взаимодействия. По аналогии с гравитационным
взаимодействием в настоящее время
введено еще три таких взаимных действия – электромагнитное, слабое и
сильное. Это, сделано не смотря на то, что не удается найти никаких
экспериментальных предпосылок для существования взаимных непосредственных
действий, т.е. не удается достоверно обнаружить физические объекты - носители
действий, и установить механизмы реализации этих действий, хотя такие попытки
неоднократно предпринимались, например, при исследовании наиболее широко
распространенного и давно исследуемого гравитационного взаимодействия. И дело
здесь вероятнее всего не в недостаточном еще развитии технологий, и не в отсутствии
пока еще достаточной квалификации физиков, а в отсутствии самих взаимных
действий (в частности, в случае гравитационных взаимодействий – в отсутствии,
так называемых, «гравитонов»). Уверенность последнему выводу придает тот
колоссальный и нерезультативный объем работ, выполненный выдающимися учеными на
протяжении достаточно длительного времени, и широчайший диапазон направлений, в
которых проводились такие исследования. Следует отметить, что иногда под
взаимодействием двух объектов понимают изменение поведения их относительно друг
друга при «излучении» или «поглощении» одним из них какого-то третьего объекта.
Представляется более корректным считать, что в таком случае имеет место не
взаимодействие одних и тех же (не меняющих свои характеристики) рассматриваемых
объектов, а вполне понятное и необходимое отличие относительного поведения пар различных
объектов (имеющих различные характеристики), каковыми они становятся в моменты
«излучения» или «поглощения» одним из них третьего объекта. Понятно, что при
этом любые изменения объекта носят дискретный характер, что подтверждается
экспериментально, и не являются континуальными изменениями, которые логичнее
было бы ожидать, если исходить из постоянно существующего «взаимодействия»
объектов в пространственно-временном континууме.
Использование
в традиционной физике таких математических понятий как система отсчета, поле,
пространственно-временной континуум, кривизна его и др. для объяснения
механизмов взаимных действий представляется искусственным и логически не
обусловленным, т.к. эти понятия не являются физическими объектами, в
соответствии с выше приведенным определением последних. Следовательно, нельзя
утверждать, что идентифицируемые с помощью этих понятий объекты являются
физическими. Интуитивный характер таких используемых понятий, т.е. отсутствие
общепринятых экспериментально подтверждаемых определений их, позволяет
вкладывать различный смысл в эти понятия и, в конечном счете, приводит к
различному осмысливанию явлений природы, что вызывает чувство неудовлетворенности
современным состоянием физической теории и тормозит прогресс в естествознании.
Вот мнение по этому поводу авторитетного французского математика и физика Анри
Пуанкаре (1854 – 1912): «Таким образом,
абсолютное пространство, абсолютное время, даже сама геометрия не имеют
характера вещей, обуславливающих собой механику; они также мало предваряют существование
механики, как мало французский язык логически предваряет существование истин,
выраженных по-французски. Можно было бы
попытаться изложить основные законы механики на языке независимом от всех этих
соглашений; тогда, без сомнения, можно бы лучше отдать себе отчет в том, что
представляют эти законы сами по себе», см. [12] стр. 64 (выделение мое
Б.Р.). Именно цели, выделенные в этой цитате, и преследует настоящая работа.
Использование ниже термина «взаимодействие»
объектов, заимствованного из традиционной физики и основанного на выше
упомянутых интуитивных понятиях, это лишь дань традиции. Под этим термином
будем понимать изменение объектов (относительных состояний или движений их)
друг относительно друга вне связи с непосредственным и целенаправленным
влиянием этих объектов на такие изменения. Смысл использования термина
взаимодействие лишь в том, чтобы качественно различать два типа относительных
изменений физических объектов - «изолированных» или «неизолированных» друг от
друга, точное определение (не связанное с непосредственным взаимным действием)
которым дано ниже.
7. Относительные состояния и
предшествование
В
соответствии с ранее указанным и априори принятым «универсальным принципом
дуализма», примем следующую аксиому. Будем считать, как это имеет место в
аксиомах порядка геометрии для точек, например, см. [13] стр. 24-25, что для
каждых двух и более объектов или двух и более качественно одинаковых
характеристик их можно установить два противоположных «направления». Эти
направления условно можно называть «положительное» и «отрицательное», и по
отношению к каждому из них любые два наблюдаемых объекта можно упорядочить в
соответствии с известным представлением о предшествовании
чего-либо в широком смысле этого слова. Аксиомы порядка справедливы не только
для объектов и характеристик их, но также и для любых качественно одинаковых
понятий, суждений, явлений и т.п. Это связано с тем, что в основе человеческого
бытия лежат те же закономерности, что и для физических объектов, хотя эти
закономерности, да и сами субъекты (люди) не полностью идентичны объектам, о
чем подробнее говориться ниже. Можно
сказать, что возможность установить «предшествование» означает существование отличия
объектов друг от друга, т.е. «предшествование» является критерием существования различимых объектов. Состояние
предшествования, которое иногда обозначают знаком « < », эквивалентно
упорядочению значений характеристик по принципу «больше - меньше», и такое предшествование
состояний не обязательно связано с понятием время. Имеет место, следующее
положение: объект предшествующий какому-нибудь объекту, который в свою очередь
предшествует в том же направлении третьему объекту, является предшествующим к
каждому из них. При таком упорядочении будем говорить о направленно
ориентированном относительном состоянии
объектов в отношении каждого из качественно одинаковых свойств их, или о
соответствующей удаленности этих объектов.
Если «направление» меняется на противоположное, то относительное состояние должно
тоже поменяться на противоположное. В зависимости от практической возможности и/или
необходимости может быть определены различные значения предшествования
– установлена различная степень, глубина, порядок и т.п. соответствующего предшествования
таких состояний. Говоря другими словами,
может быть установлено многократное «предшествование предшествованию» состояний
объектов. Это обуславливается тем, насколько детально можно/нужно идентифицировать
относительные состояния их а, следовательно, и сами объекты. Как это
практически осуществляется применительно к физическим объектам, будет указано
ниже – после определения фундаментальных характеристик их и понятия наблюдение
за изменением объектов.
Предварительно
укажем, что существуют (будем постулировать это) два значения предшествования
каждых двух относительных состояний, называемые ниже относительные экстремумы, за пределами которых
существования предшествования нельзя практически установить. Эти два значения
могут быть получены при монотонном изменении предшествования двух объектов,
т.е. таком, при котором меняется лишь величина предшествования - меняется лишь
численные значения характеристик, но не сами объекты (не их качество и их
число). На определенных этапах таких изменений пропадает возможность определять
относительное состояние этих объектов, что можно рассматривать как переход пары
их в другое качество. Отсутствие возможности фактически установить
предшествование объектов в каком-либо отношении (что эквивалентно отсутствию
возможности различать соответствующие характеристики их) может означать, что
речь может идти только о предшествовании
их другим объектам. Указанные ситуации наступают в двух случаях – при
монотонном увеличении и монотонном уменьшении соответствующего предшествования.
Заметим, что в этих предельных случаях пропадает и смысл определения относительных
состояний таких объектов, т.к. любые суждения (в том числе и прямо противоположные)
об этих состояниях одинаково достоверны, из-за не возможности экспериментально
подтвердить их или опровергнуть. Существование экстремумов является
фундаментальной ограничительной закономерностью естествознания, о чем уже
говорилось ранее, когда указывалось, что однозначно определять и сравнивать
между собой можно только такие понятия (характеристики), которые допустимо
осмысливать как нечто конечное и единое. Экстремумы имеют место при любом предшествовании
как физических, так и математических объектов, и при осмысливании любых понятий
и суждений и т.п. По-видимому, это связано с тем, что в масштабах вселенной все
объекты и субъекты являются «конечномерными», т.е. характеристики их имеют
конечные значения. В силу этого существует «горизонт»,
обуславливающий существования двух экстремумов (для возрастания и для
уменьшения), за пределами которых принципиально невозможно установить
предшествование. Для различных объектов и субъектов эти экстремумы могут
отличаться количественно, но они всегда существуют. Этому существованию обязаны
и то, что не возможно с необходимой точностью осмыслить понятие «пространственно-временного
континуума», и вытекающие из этого проблемы традиционной физики.
Для
трех и более физических объектов можно установить помимо предшествования каждых
двух объектов друг другу еще и предшествование друг другу состояний различных
пар объектов, которых в этом случае будет уже больше чем одно. Предшествование
друг другу относительных состояний разных пар объектов, которое может иметь
место только для системы не менее трех физических объектов, назовем физическим состоянием такой системы объектов.
Понятно, что и для каждой пары физических состояний могут быть установлены многократные
предшествования предшествований их друг другу. Тем самым можно последовательно
сравнивать (упорядочивать) состояния любого числа физических объектов и систем
их, а также и любые степени отличия их друг от друга. Способы фиксирования
предшествований связаны с «механизмами» памяти, и являются индивидуальными для
разных объектов и субъектов. В одних случаях субъекты используют только свою
внутреннюю память, а в других – еще и внешнюю память, и при этом существенную
роль играют масштабы, определение которым дано ниже. В любом случае для
фиксирования предшествования или для реализации «механизма» памяти необходимо
не менее трех объектов (систем их), два из которых должны служить для сравнения
с ними любых других пар. В определенном смысле возможность различать относительные
состояния объектов эквивалентна существующему в геометрии понятию «движение»,
которое позволяет производить сравнения между собой отрезков и углов путем
наложениях их друг на друга. Таким образом, изменение возможно благодаря
существованию предшествования. Допустимо утверждать и обратное - предшествование
существуют благодаря тому, что возможно изменение. Отсюда следует, что все физические объекты (их пары), которые могут
быть наблюдаемы, потенциально могут быть упорядочены субъектом друг
относительно друга, по крайней мере, опосредствованно. Впрочем, что касается упорядочения
абсолютно всех объектов и предшествований их, то это имеет чисто теоретическое
значение, т.к. практически, имеет смысл говорить только о незначительном числе
объектов и предшествований, из-за существования вышеуказанных двух «экстремумов».
Относительные изменения физических состояний объектов, назовем физическим процессом. Такие изменения
являются необходимым условием возможности наблюдения за этими объектами, можно
сказать – существования их. Это перекликается с известным изречением Джорджа
Беркли (1685 – 1753): «Существовать –
значит быть воспринимаемым». Не будь изменений, не только нельзя было бы
наблюдать за объектами – изучать природу, но и не было бы в этом нужды как,
например, не было бы смысла следить за объемом бензина в баке автомобиля, если
бы этот объем никогда не мог бы меняться. Известно, что некоторые насекомые, животные,
а также люди используют это свойство (временно не совершают никаких изменений
ни в чем) для того, чтобы обмануть своих врагом и попытаться убедить их в
нецелесообразности наблюдений за собой, и тем самым сохранить свою жизнь или
лишить ее других.
Существование
предшествования находит отражение в имеющемся в естествознании понятии
причинно-следственная связь. Под причиной
понимают такое состояние или процесс, изменение которого предшествует
определенному изменению другого состояния или
процесса, называемого следствием, и
при этом нет необходимости/возможности (скорее всего пока) определять иное
предшествующее следствию состояние, изменение которого приводит к такому же
изменению следствия. В случае появления у субъекта необходимости/возможности определить
такое состояние, оно и будет причиной. Понятно, что при изменении «направления»
предшествования причина становиться следствием, а следствие причиной. Процессы
и состояния, не имеющие причины (на разных этапах развития цивилизации таковыми
считались различные процессы и состояния) и, следовательно, не могущие быть
измененными, называется соответственно фундаментальными
процессами (законами) и состояниями природы. Таким образом, эти состояния и
законы не являются следствиями существования чего-либо другого и не могут быть
причиной существования других фундаментальных состояний и законов. В этом
смысле фундаментальные законы абсолютны и автономны – не зависят ни от
кого-либо, ни от чего-либо. Формально допустимо говорить, что каждый
фундаментальный закон или состояние природы являются причиной и следствием лишь
самих себя, т.к. они не связаны с другими законами или состояниями. В тоже
время, все иные (не фундаментальные) законы и состояния потенциально являются
причинами и/или следствиями друг друга. В математике понятию
причинно-следственной связи соответствует понятие
функциональной зависимости. Причина соответствует аргументу, а следствие –
функции. Знание и изменение аргумента всегда предшествует знанию и изменению
функции. Можно сказать, что это и является определением аргумента и функции,
которые могут меняться местами (по аналогии с причиной и следствием) в
зависимости от потребности или удобства этого для субъекта.
Как
уже сказано, для описания поведения физических объектов, определенных выше
приведенным образом, подходы традиционной физики не годятся. Действительно,
согласно этим подходам для идентификации объектов (определения их свойств,
указания положения, состояния и т.п.) используется так называемый
пространственно–временной континуум (метрическое пространство и время), не
являющийся согласно принятому определению физическим объектом.
Пространственно-временной континуум это сугубо математическое понятие, существование
которого не связано с физическими объектами, хотя и принимают, что они
«расположены» (?) в континууме. Понятие «интервал», характеризующее континуум,
а также понятие «расстояние» между точками континуума, используемое при
определении «интервала», являются тоже чисто математическими и считаются
априори известными и независящими от свойств и даже от наличия или отсутствия
физических объектов в континууме. Они являются понятиями, определяемыми
мгновенно (вычисляемыми по так называемым координатам, а не получаемыми в
результате выполнения какого-нибудь физического процесса с затратой времени),
например, см. [3]. Таким образом, использование пространственно-временного
континуума для идентификации объектов может считаться корректным только, если
идентифицируемые объекты являются математическими. Поэтому не следует ожидать,
что в рамках традиционного подхода удастся удовлетворительно описать
фактическое поведение физических объектов не только количественно (с
необходимой точностью), но в некоторых случаях и качественно. Например, - описать
с единых позиций электромагнитные, термодинамические, химические и т.п. явления
без отказа от присвоения физическим объектам, априори не свойственных им математических
свойств. Ниже будет показано, что описание любых физических явлений, например,
гравитационных, электромагнитных, термохимических или иных может быть выполнено
без использования понятия поле и пространственно-временного континуума,
являющихся основополагающими понятиями традиционной физики, и без искусственного
приписывания физическим объектам свойств, отличающихся от выше указанных фундаментальных
свойств их. Тем самым будет сделан существенный шаг в решении вопроса о
существовании Единой Теории Естествознания.
Понятия
метрического пространства и времени, использовались механикой Ньютона как
самостоятельные и не связанные ни с чем другим, см. [17]. Т.е. использовались как
понятия, не зависящие ни друг от друга, и ни от физических объектов лишь существующих
и изменяющихся в пространстве и во времени. Другими словами, объекты никак не
влияют на пространство и время и не испытывают влияние их. Такой подход предполагает
неявным образом существование какого-то «абсолютно неподвижного и недеформируемого
материального носителя», в/на котором якобы находятся физические объекты. И
этот «носитель» как раз и служит лишь для мгновенного (вне понятия времени)
определения расстояния между объектами путем математических вычислений с использованием
их координат. Для объектов расположенных на земле роль такого «носителя» играла
поверхность земли, на которой можно устанавливать неподвижные друг относительно
друга (неизменяемые во времени) масштабные «метки» (верстовые столбы, различные
указатели и т.п.). Для космических объектов роль такого «носителя» стали предписывать
без какого-нибудь экспериментального обоснования некой гипотетической субстанции,
ранее называемой эфиром, а ныне называемой «метрическим пространством» или «физическим
вакуумом» (!?), в котором существуют поля. Принятие физикой указанного подхода
имело цель соблюсти единообразие построения математики и физики. Оно было
обусловлено не только субъективными обстоятельствами, связанными с тем, что обе
эти науки создавались, можно сказать, одновременно и параллельно одними и теми
учеными, - но и объективными причинами. Действительно, принятые положения
позволяли в большинстве случаев достаточно корректно описывать поведения
объектов на единственно доступном для существовавших в те времена технологий макро
уровне. «Сегодня мы с трудом понимаем,
почему интуитивные представления о пространстве и времени считались столь
заслуживающими внимания. К счастью, аналитическая геометрия Декарта явилась
средством, позволявшим избавиться от этих интуитивных представлений и заменить
их числами, т.е. одними лишь символами». Это и следующее – более категоричное высказывание по этому
вопросу, принадлежит ранее цитированному Г. Вейлю, см. [1] стр.74 и 93: «Напротив, я придерживаюсь здесь того
взгляда, что здание анализа в значительной мере возведено на песке». Здесь
уместно напомнить уже указанное выше (в первой главе), что предложенные
Ньютоном подходы были достаточно критически восприняты практически всем
существовавшим в то время научным
сообществом.
Предпринимаемые
в течение всего последующего времени попытки модернизировать эти подходы,
сохраняя при этом их математическую сущность, не дали ожидаемого результата,
т.е. не привели к созданию Единой Теории Естествознания, позволяющей описывать
с единых позиций поведение физических объектов на микро и макро уровнях.
Уверенность в существовании такой Единой Теории, разделяемая практически всеми
учеными в области естествознания, основывается на том, что ранее естествознанию
вообще, и физике в частности, удавалось находить общие фундаментальные
закономерности, позволяющие описывать с единых позиций различные явления.
Достижения этой цели, по-видимому, возможны при более радикальных изменениях
физики, о которых говорится ниже. Речь идет, во-первых, об отказе от использования
для идентификации физических объектов чего-либо другого кроме их самих. В
частности, об отказе от использования такого математического понятия как
метрическое пространство и связанного с ним понятия пространственно-временной
континуум. Во-вторых, об отказе от чисто эмпирического построения физики и
переходе к полностью аксиоматическому построению, как это имеет место в
геометрии, которая тоже начиналась как наука о наблюдениях. Заметим, что Давид Гильберт
(1862 – 1943), один из самых выдающихся математиков ХХ века, утверждал в 1930 году, что геометрия – часть
физики. Тем самым можно сказать, что Гильберт не исключал возможность
аксиоматического построения физики. Кстати, при самом аксиоматическом
построении геометрии понятие пространства не используется, оно может быть
использовано лишь при каких-то реализациях геометрии, в частности, - при
декартовой реализации. Если глубже проанализировать причину возникновения и
существования понятий пространства и времени, как их использовал Ньютон, то
можно прийти к выводу, что эти понятия фактически были обусловлены еще и
господствовавшим в те времена представлением (полностью от него не отказались и
сейчас) о непрерывности и безграничности материи. Т.е. представлениями о том,
что на фундаментальном уровне материя не имеет ни внутренних, ни внешних
границ, за которыми материя отсутствует. Существуют лишь скопления материи,
называемые материальными объектами, где плотность материи гораздо выше средней.
Совершенно очевидно, что при таких представлениях для описания изменения
материи необходимо было искусственно ввести понятие чего-то внешнего и
неизменного по отношению к материи, что и было сделано введением
математического понятия «метрическое пространство». Если же отказаться от
гипотезы о том, что материя непрерывна и безгранична, а результаты современных
экспериментов указывают на обоснованность такого отказа, и принять, что материя
дискретна, то отпадает необходимость искусственно вводить и использовать
нематериальный объект – «пространственно-временной континуум». При этом для
описания изменений материальных объектов можно использовать другие материальные
объекты, относительно которых любые изменения объектов только и можно наблюдать.
Ниже сделана попытка, продемонстрировать, что такой подход позволяет достаточно
корректно построить физику, способную описывать с единых позиций более широкий
круг явлений, чем это допускает традиционная физика.
Глава 3. Суть аксиоматического подхода к физике
1. Фундаментальные характеристики физического объекта
Поскольку
физический объект, как уже указывалось, является составным и обладает не только
качеством, но и количеством соответствующего качества, то он должен иметь более
чем одну характеристику, в отличие от математического объекта, обладающего только
качеством. Для однозначного определения всех характеристик физического объекта
необходимо наблюдать такую систему объектов, одним из которых является он сам (или
систему составляющих его частей), которая позволяет эти характеристики получать.
В такой системе число (конечное) различных пар объектов должно совпадать с
числом самих этих объектов. При этом относительные состояния всех пар объектов
однозначно определят искомые характеристики этих объектов или удаленности каждой
пары их а, следовательно, и самого физического объекта, который они составляют.
Не трудно убедиться, что такой особенностью обладает лишь система из трех
объектов, характеризующаяся тремя состояниями пар их. Действительно – система
двух объектов имеют одну пару, система четырех объектов – 6 пар, система пяти
объектов – 10 пар и т.д. Учитывая то, что любой физический объект можно
рассматривать как систему объектов, число однозначно идентифицирующих такой объект
характеристик должно совпадать с соответствующим числом пар объектов
составляющих его, т.е. должно равняться трем. Эти три
характеристики являются зависимыми друг от друга, т.к. определяются в результате
рассмотрения общей системы их, и не могут отличаться количественно, т.к.
характеризуют один и тот же составной объект. Они отличаются качественно, хотя
и должны определяться тремя принципиально
не отличающимися друг от друга способами наблюдения за тремя парами объектов.
Здесь имеет место ранее указанный закон перехода количества в качество,
обуславливающий связь между собой всех свойств объекта, каждое из которых определяется
как количеством, так и качеством составляющих его объектов. Если ограничиться
рассмотрением явлений, которые осмысливаются в рамках трех априори существующих
для нас объективных восприятий протяженности, длительности и материальности
(восприятия количества или возможности считать наблюдаемые объекты) то три выше
упомянутые характеристики объектов и
удаленностей пар их, однозначно идентифицирующие все физические объекты,
участвующие в этих явлениях, можно ассоциировать с этими понятиями. С учетом
этого, характеристики объектов и удаленности двух из них друг от друга будем
называть, и обозначать: пространственная - ![]() и
и ![]() , временная -
, временная - ![]() и
и ![]() , и материальная -
, и материальная -
![]() и
и ![]() , где индексы у
удаленностей указывают на то, что эта характеристика двух объектов
, где индексы у
удаленностей указывают на то, что эта характеристика двух объектов ![]() и
и ![]() . Иногда говорят, что объекты отличаются друг от друга в
пространственном, временном или материальном отношении, что эквивалентно тому,
что между ними существуют (не равные нулю) соответствующие удаленности. Физический смысл этих характеристик заключается в том,
что они позволяют отвечать на следующие три вопроса, без которых не возможна
идентификация материальных объектов друг относительно друга: «как далеко», «как
быстро (или как часто)», «как много». Любые физические объекты и удаленности
любых пар их должны иметь эти три характеристики. Каждая из этих характеристик
не может быть осмыслена без осмысливания
двух других, и должна рассматриваться как компонент единой (трехкомпонентной)
системы. Заметим, что в случае рассмотрения эксклюзивных явлений, например,
различных экзотических явлений с участием не материальных объектов духовного
(или эзотерического) мира, то для того, чтобы такое рассмотрение имело бы хоть какой-нибудь смысл, т.е. не было
бы бесплодным, их характеристики должны быть связаны с другими, способными быть
осмысленными, понятиями. Очевидно, что эти понятия должны быть формализованы не
в меньшей степени, чем обычные материальные понятия. Выбор того, какие объекты:
материальные, нематериальные или и те, и другие допустимо рассматривать,
определяется тем, насколько полно можно/нужно описать интересующие явления
(понятия) соответствующими объектами. Ниже речь идет только о материальных
явлениях физического мира.
. Иногда говорят, что объекты отличаются друг от друга в
пространственном, временном или материальном отношении, что эквивалентно тому,
что между ними существуют (не равные нулю) соответствующие удаленности. Физический смысл этих характеристик заключается в том,
что они позволяют отвечать на следующие три вопроса, без которых не возможна
идентификация материальных объектов друг относительно друга: «как далеко», «как
быстро (или как часто)», «как много». Любые физические объекты и удаленности
любых пар их должны иметь эти три характеристики. Каждая из этих характеристик
не может быть осмыслена без осмысливания
двух других, и должна рассматриваться как компонент единой (трехкомпонентной)
системы. Заметим, что в случае рассмотрения эксклюзивных явлений, например,
различных экзотических явлений с участием не материальных объектов духовного
(или эзотерического) мира, то для того, чтобы такое рассмотрение имело бы хоть какой-нибудь смысл, т.е. не было
бы бесплодным, их характеристики должны быть связаны с другими, способными быть
осмысленными, понятиями. Очевидно, что эти понятия должны быть формализованы не
в меньшей степени, чем обычные материальные понятия. Выбор того, какие объекты:
материальные, нематериальные или и те, и другие допустимо рассматривать,
определяется тем, насколько полно можно/нужно описать интересующие явления
(понятия) соответствующими объектами. Ниже речь идет только о материальных
явлениях физического мира.
Понятно,
что любая система материальных объектов, если ее рассматривать, как один материальный
объект, тоже должна иметь такие три характеристики и, следовательно, теоретически
может быть представлена тремя своими материальными частями – материальными
объектами. Если исходить из того, что какой-то объект состоит из более трех материальных
объектов, то этот составной объект может характеризоваться еще и другими
свойствами, например, температурой, энтропией, спином, электрическим и
магнитным зарядом, химическими свойствами и др., которые можно интерпретировать
как производные от трех указанных
характеристик. С учетом этого, пространственную, временную и материальную характеристики
будем называть фундаментальными характеристиками объекта (системы их).
Подчеркнем еще раз, что для определения их не нужно использовать никаких других
дополнительных понятий кроме понятий объект и субъект. Например, не требуется
вводить (предполагать физическое существования) и использовать следующие не
являющиеся физическими понятия традиционной физики: система отсчета, силовое
поле, пространственно-временной континуум. Ниже показано, что с помощью трех
фундаментальных характеристик может быть описано не только гравитационное
поведение материального макро объекта и систем их, но и электромагнитные, и
релятивистские, и даже внутри атомные явления. И во всех этих случаях
достаточно рассматривать системы соответствующего числа объектов только с этими
фундаментальными характеристиками. Как следует из многочисленных
экспериментальных данных, любое поведение материального объекта зависит, в
конечном счете, только от существования (практической возможности фиксирования
такого существования) других объектов и ни от чего-либо другого. Понятно, что
сказанное по поводу использования только трех фундаментальных характеристик не
отрицает возможность рассмотрения в некоторых случаях поведение системы
большого числа объектов как единого объекта, обладающего еще и какими-либо не
указанными выше фундаментальными характеристиками (например, электрическими,
магнитными, химическими, тепловыми и т.п.), если это упрощает рассмотрение
соответствующих явлений.
Необходимо
подчеркнуть следующее принципиальное положение. Понятие предшествования имеет
смысл и введено выше только для таких объектов и суждений, которые практически возможно
и необходимо отличить друг от друга – считать различными. Для частей одного
объекта, различать которые практически нет возможности или необходимости (иначе
их можно было бы рассматривать как самостоятельные объекты), но в существование
этих частей верят исходя из косвенных данных, понятие предшествование их не имеет
смысла. Следовательно, изменения трех разных фундаментальных характеристик
одного и того же объекта не могут предшествовать друг другу, а определение этих
характеристик не является физическим процессом, который выше определен как относительные
изменения физических состояний ни менее трех разных объектов.
Определение фундаментальных характеристик объекта, если оно осуществляется без
привлечения внешних для него объектов – путем рассмотрения внутренних частей самого объекта,
будем называть процедурой. Процедура
является предельным случаем физического процесса и ее можно называть математическим процессом, поскольку,
как будет показано ниже, и саму математику можно рассматривать как предельный
случай физики. Говоря языком традиционной физики, процедура реализуется вне
времени и без изменений в пространстве, в отличие от процесса, который осуществляется с затратой времени и
происходит в пространстве. Иногда, если хотят подчеркнуть, что что-либо
произошло или может произойти без затраты времени и без изменений в
пространстве (как это имеет место в процедурах), то это называют событиями. Следует иметь в виду, что
понятия «длительность», «протяженность» и «материальность» иногда применяются
не только к составным (физическим) объектам, но и к конечным физическим
процессам, в которых участвуют не менее трех физических объектов. Можно сказать,
что этим определяется или это само определяет смысл, вкладываемый в понятия
«длительность», «протяженность» и «материальность». Следует указать, что поскольку
процедуры совершаются в отношении различных физических объектов, то для таких процедур
тоже может быть установлено предшествование их друг другу.
3. Точки и пространственная
удаленность их
Указанные
выше три фундаментальные характеристики физического объекта можно представлять
координатами его в трехмерном «характеристическом пространстве». Это
пространство является логически мыслимым («пространством
представлений» по терминологии А. Пуанкаре) и, следовательно, оно не влияет на физические объекты
и не испытывает никакого влияния их. Отличается оно от пространств Евклида и
Минковского тем, что все три координаты имеют различный физический смысл
(описывают качественно различные свойства объектов) и не могут быть независимыми
друг от друга. Точкой такого
трехмерного пространства будем называть три связанных между собой вещественных
числа ![]() являющихся координатами
ее в «характеристическом пространстве», т.е. представляющих трехкомпонентную
систему характеристик точки/объекта. С учетом этого, термины «точка» и «объект»
ниже могут рассматриваться как эквивалентные, если это специально не оговорено.
На основании всего выше изложенного, удается построить физику аксиоматически, и
использовать идеологию и даже терминологию геометрии. Дадим определения
физическим понятиям прямая и окружность, неоднократно используемым в дальнейшем.
Заметим, что в математике эти понятия являются частным случаем понятия «линия»,
формулировка которого является довольно не простым делом, см. [7], т.3 стр.382: «Линия – геометрическое понятие, точное и в
тоже время достаточно общее определение, которого представляет значительные
трудности и осуществляется в разных разделах геометрии различно». Будем
говорить, что две точки однозначно определяют единственную прямую, а три точки – единственную окружность, на которых могут лежать и более соответственно двух и
трех точек, или говорить, что прямая и окружность проходят через все эти точки.
Можно говорить, что каждая прямая и окружность имеют в рассматриваемом
трехмерном «характеристическом пространстве» три «проекции» или состоят из трех
«прямых» и «окружностей» - пространственной, временной и материальной. Ниже
речь будет идти только о пространственных прямых и окружностях, если иное специально
не указано. Три точки лежат на одной прямой, если пространственная удаленность
какой-нибудь пары их равняется сумме удаленности двух других их пар. Три точки
лежат на одной окружности, если квадрат пространственной удаленности какой-нибудь
пары их (такая удаленность называется диаметр окружности) равен сумме квадратов
удаленности двух других пар точек. Способ определения пространственной
удаленности двух точек друг относительно друга будет указан ниже после того,
как будет определено понятие наблюдения
за объектами. Часть прямой лежащей между двумя точками M и Q будем называть отрезком, а пространственную удаленность этих двух точек M и Q
будем называть расстоянием
между ними или длиной отрезка и обозначать
являющихся координатами
ее в «характеристическом пространстве», т.е. представляющих трехкомпонентную
систему характеристик точки/объекта. С учетом этого, термины «точка» и «объект»
ниже могут рассматриваться как эквивалентные, если это специально не оговорено.
На основании всего выше изложенного, удается построить физику аксиоматически, и
использовать идеологию и даже терминологию геометрии. Дадим определения
физическим понятиям прямая и окружность, неоднократно используемым в дальнейшем.
Заметим, что в математике эти понятия являются частным случаем понятия «линия»,
формулировка которого является довольно не простым делом, см. [7], т.3 стр.382: «Линия – геометрическое понятие, точное и в
тоже время достаточно общее определение, которого представляет значительные
трудности и осуществляется в разных разделах геометрии различно». Будем
говорить, что две точки однозначно определяют единственную прямую, а три точки – единственную окружность, на которых могут лежать и более соответственно двух и
трех точек, или говорить, что прямая и окружность проходят через все эти точки.
Можно говорить, что каждая прямая и окружность имеют в рассматриваемом
трехмерном «характеристическом пространстве» три «проекции» или состоят из трех
«прямых» и «окружностей» - пространственной, временной и материальной. Ниже
речь будет идти только о пространственных прямых и окружностях, если иное специально
не указано. Три точки лежат на одной прямой, если пространственная удаленность
какой-нибудь пары их равняется сумме удаленности двух других их пар. Три точки
лежат на одной окружности, если квадрат пространственной удаленности какой-нибудь
пары их (такая удаленность называется диаметр окружности) равен сумме квадратов
удаленности двух других пар точек. Способ определения пространственной
удаленности двух точек друг относительно друга будет указан ниже после того,
как будет определено понятие наблюдения
за объектами. Часть прямой лежащей между двумя точками M и Q будем называть отрезком, а пространственную удаленность этих двух точек M и Q
будем называть расстоянием
между ними или длиной отрезка и обозначать ![]() . Расстояния между объектами, являющимися составными частями
одного и того же объекта, называются размерами
его.
. Расстояния между объектами, являющимися составными частями
одного и того же объекта, называются размерами
его.
Уточним
и другие заимствованные из геометрии термины, ниже используемые при построении
физики. Будем говорить, что две прямые, каждая из которых проходит через две из
трех точек m, M, Q, не лежащих на
одной прямой, однозначно идентифицируют единственную плоскость, на которой лежат эти прямые. Каждые из этих двух прямых
имеют свои пространственные направления в этой плоскости, которые могут быть определены
лишь друг относительно друга, для чего используется понятие угла. При этом говорят, что углы
количественно характеризуют относительно друг друга пространственные направления
прямых, образующих эти углы. В свою очередь, угол количественно определяется расстоянием
между двумя точками, каждая из которых расположена на одной из двух
рассматриваемых прямых, и расстояниями этих точек до общей для этих двух прямых
точки пересечения их. Такие прямые называются пересекающимися прямыми и любые две из них образуют четыре пары
смежных друг другу углов, лежащих в этой плоскости. Углы измеряются в градусах
или радианах и сумма четырех углов, образуемых двумя пересекающимися прямыми,
всегда равна 3600 или ![]() радиан. Понятно, что
на плоскости могут лежать и более двух прямых, имеющие отличающиеся друг от
друга пространственные «направления». Три из них определяемые точками m, M, Q идентифицируют
треугольник
радиан. Понятно, что
на плоскости могут лежать и более двух прямых, имеющие отличающиеся друг от
друга пространственные «направления». Три из них определяемые точками m, M, Q идентифицируют
треугольник ![]() лежащий в этой
плоскости. В треугольнике имеются три внутренних угла обозначаемых ниже
лежащий в этой
плоскости. В треугольнике имеются три внутренних угла обозначаемых ниже ![]() . Если один из внутренних углов, образуемых какими-нибудь
двумя сторонами треугольника, например, сторонами
. Если один из внутренних углов, образуемых какими-нибудь
двумя сторонами треугольника, например, сторонами ![]() и
и ![]() , принимает нулевое
значение или значение 1800 или
, принимает нулевое
значение или значение 1800 или ![]() , то это означает, что эти прямые становятся одной прямой и
треугольник вырождается в эту прямую. При этом на этой прямой лежат все три
точки m, M, Q, и точка m лежит – во
втором случае между точками M и Q – внутри отрезка
, то это означает, что эти прямые становятся одной прямой и
треугольник вырождается в эту прямую. При этом на этой прямой лежат все три
точки m, M, Q, и точка m лежит – во
втором случае между точками M и Q – внутри отрезка ![]() , а в первом случае – вне отрезка. По аналогии с прямым могут
существовать две плоскости пересекающиеся друг с другом, но при этом они должны
иметь более чем одну общие точки, лежащие на единой прямой. Каждые из двух
таких плоскостей тоже имеют свои пространственные «направления», которые могут
быть идентифицированы лишь друг относительно друга и тоже с помощью угла.
Прямые или плоскости, не имеющие ни одной общей точки, называются параллельными. Пространственные
направления их не могут быть идентифицированы друг относительно друга с помощью
угла. Формально можно говорить, что угол между параллельными прямыми или
плоскостями отсутствует или равен нулю.
, а в первом случае – вне отрезка. По аналогии с прямым могут
существовать две плоскости пересекающиеся друг с другом, но при этом они должны
иметь более чем одну общие точки, лежащие на единой прямой. Каждые из двух
таких плоскостей тоже имеют свои пространственные «направления», которые могут
быть идентифицированы лишь друг относительно друга и тоже с помощью угла.
Прямые или плоскости, не имеющие ни одной общей точки, называются параллельными. Пространственные
направления их не могут быть идентифицированы друг относительно друга с помощью
угла. Формально можно говорить, что угол между параллельными прямыми или
плоскостями отсутствует или равен нулю.
В
треугольнике, рассматриваемом как единый объект (а не как систему трех несвязанных
друг с другом отрезков или объектов),
всегда имеют место следующие экспериментально подтверждаемые соотношения между
размерами трех его сторон ![]() и его углами. Заметим,
что в рассматриваемом случае определение всех трех размеров является одной
процедурой, а не тремя различными процессами, предшествующими друг другу. Эти соотношения состоят в том, что размер
каждой из сторон треугольника равен сумме размеров двух других сторон его,
нормированных коэффициентами, называемыми косинусами углов между этой стороной
и соответствующими сторонами. Численные значения любого из трех этих коэффициентов
обозначаемых
и его углами. Заметим,
что в рассматриваемом случае определение всех трех размеров является одной
процедурой, а не тремя различными процессами, предшествующими друг другу. Эти соотношения состоят в том, что размер
каждой из сторон треугольника равен сумме размеров двух других сторон его,
нормированных коэффициентами, называемыми косинусами углов между этой стороной
и соответствующими сторонами. Численные значения любого из трех этих коэффициентов
обозначаемых ![]() ,
, ![]() и
и ![]() не превосходят по
модулю единицы. Указанные соотношения имеют вид:
не превосходят по
модулю единицы. Указанные соотношения имеют вид:
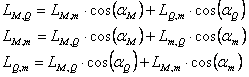 (1)
(1)
Можно
сказать, что вышеуказанные соотношения являются фундаментальным законом, и мы в
дальнейшем будем неоднократно его использовать. Физический смысл этих
соотношений можно интерпретировать как выражение непрерывности
«характеристического пространства», в котором возможно существование
треугольника как единого объекта, а не как системы трех несвязанных друг с
другом отрезков, т.е. возможна идентификация треугольника. Если один из
коэффициентов равен нулю, например ![]() =0, то сумма квадратов двух других коэффициентов равна
единице. Угол соответствующий нулевому коэффициенту равен
=0, то сумма квадратов двух других коэффициентов равна
единице. Угол соответствующий нулевому коэффициенту равен ![]() или
или ![]() и называется прямым, а
треугольник, имеющий такой угол, называется прямоугольным. Все три точки m, M, Q такого
треугольника, называемые вершинами треугольника, лежат на одной окружности. Отрезок
МQ является
диаметром этой окружности –
наибольшим отрезком, соединяющим две точки окружности. Если один из
коэффициентов равен минус единице (угол соответствующий ему равен 1800
или
и называется прямым, а
треугольник, имеющий такой угол, называется прямоугольным. Все три точки m, M, Q такого
треугольника, называемые вершинами треугольника, лежат на одной окружности. Отрезок
МQ является
диаметром этой окружности –
наибольшим отрезком, соединяющим две точки окружности. Если один из
коэффициентов равен минус единице (угол соответствующий ему равен 1800
или ![]() ), то два других коэффициента равны единице (соответствующие
им углы равны нулю). Это соответствует выше указанному случаю, когда
треугольник вырождается в прямую. Произведение отрезка (его длины) на косинус
угла между ним – и другой прямой называется проекцией отрезка на соответствующую прямую. С учетом этих
определений, можно говорить, что сторона треугольника равна сумме проекций на
нее двух других сторон. В прямоугольном треугольнике квадрат размера стороны,
лежащей против прямого угла и называемой гипотенузой (как указывалось выше, она
является диаметром окружности, на которой лежат все три этих точки), равен
сумме квадратов размеров двух других сторон треугольника называемых катетами.
Это соотношение называется теоремой Пифагора.
), то два других коэффициента равны единице (соответствующие
им углы равны нулю). Это соответствует выше указанному случаю, когда
треугольник вырождается в прямую. Произведение отрезка (его длины) на косинус
угла между ним – и другой прямой называется проекцией отрезка на соответствующую прямую. С учетом этих
определений, можно говорить, что сторона треугольника равна сумме проекций на
нее двух других сторон. В прямоугольном треугольнике квадрат размера стороны,
лежащей против прямого угла и называемой гипотенузой (как указывалось выше, она
является диаметром окружности, на которой лежат все три этих точки), равен
сумме квадратов размеров двух других сторон треугольника называемых катетами.
Это соотношение называется теоремой Пифагора.
Справедливость
указанных выше соотношений для квадратов косинусов углов и размеров сторон прямоугольного
треугольника легко может быть прослежена исходя из равенств (1). Действительно,
подставляя в правую часть первого из этих равенств значения для размеров сторон
из второго и третьего равенств (с учетом ![]() =0), получим первое из выше указанных соотношений для
квадратов косинусов углов. Умножая второе равенство на
=0), получим первое из выше указанных соотношений для
квадратов косинусов углов. Умножая второе равенство на ![]() , а третье равенство на
, а третье равенство на ![]() и складывая эти
произведения, получим (с учетом первого равенства) теорему Пифагора. Заметим,
что выше полученные для прямоугольного треугольника соотношения применяются для
практических вычислений самих углов и
косинусов их с использованием размеров сторон треугольника. Как уже говорилось,
углы характеризуют так называемые пространственные направления прямых, образующих
эти углы, относительно друг друга и количественно определяются удаленностью
между двумя точками, каждая из которых расположена на одной из двух
пересекающихся прямых, и расстояниями этих точек до общей для этих двух прямых
точки пересечения. Таким образом, используя понятие пространственной
удаленности, можно осмыслить и однозначно определить такие понятия как
относительные пространственные направления двух прямых и двух плоскостей, а
также и следующие, связанные друг с другом понятия. Ими являются: расположение
точки, не лежащей на прямой по отношению ней; расположение точки вне плоскости
по отношению к ней; упорядочение расположения трех точек, не принадлежащих
одной прямой. Каждое из этих понятий имеет два значения, которым будем
приписывать знаки « + » или « - » и
называть соответственно: «слева или справа» от прямой; «над или под» плоскостью;
«по или против часовой стрелке» расположены (упорядочены) три точки. Связь этих
понятий между собой проявляется в том, что при изменении знака одного понятия
меняется знак другого понятия, как это показано ниже.
и складывая эти
произведения, получим (с учетом первого равенства) теорему Пифагора. Заметим,
что выше полученные для прямоугольного треугольника соотношения применяются для
практических вычислений самих углов и
косинусов их с использованием размеров сторон треугольника. Как уже говорилось,
углы характеризуют так называемые пространственные направления прямых, образующих
эти углы, относительно друг друга и количественно определяются удаленностью
между двумя точками, каждая из которых расположена на одной из двух
пересекающихся прямых, и расстояниями этих точек до общей для этих двух прямых
точки пересечения. Таким образом, используя понятие пространственной
удаленности, можно осмыслить и однозначно определить такие понятия как
относительные пространственные направления двух прямых и двух плоскостей, а
также и следующие, связанные друг с другом понятия. Ими являются: расположение
точки, не лежащей на прямой по отношению ней; расположение точки вне плоскости
по отношению к ней; упорядочение расположения трех точек, не принадлежащих
одной прямой. Каждое из этих понятий имеет два значения, которым будем
приписывать знаки « + » или « - » и
называть соответственно: «слева или справа» от прямой; «над или под» плоскостью;
«по или против часовой стрелке» расположены (упорядочены) три точки. Связь этих
понятий между собой проявляется в том, что при изменении знака одного понятия
меняется знак другого понятия, как это показано ниже.
4.
Элементарные изменения и их наблюдение
Укажем
теперь, как без использования традиционных понятий («пространственно-временной
континуум», «взаимодействия», «системы отсчета», «координаты» и др.) фактически
определяются изменения физических объектов. Т.е. как субъекты реально фиксируют
изменения объектов, и тем самым определяют их самих, поскольку изменения являются,
как указано выше, необходимыми условиями идентификации объектов - существования
их. Ранее уже говорилось, что простейшие и поэтому наиболее достоверно
фиксируемые изменения любой наблюдаемой системы объектов или, что тоже, изменения
любого физического объекта (как сказано выше любой объект является частью какой-то
системы объектов или сам представляет собой систему объектов) - это следующие два противоположных события. Эти
события, при которых происходит увеличение и уменьшение количества наблюдаемых объектов
на единицу, т.е. возникновение и исчезновение одного объекта, ранее названы
соответственно рождение или излучение и смерть или поглощение этого объекта.
Оба указанных события количественно симметричны, т.е. если одно событие
количественно меняет состояние системы, то противоположное – восстанавливает
его. Для того чтобы практически фиксировать эти события участвующие в них объекты
должны находиться достаточно «близко» друг к другу. Ниже будет раскрыт
физический смысл этого понятия и обоих указанных событий. Кратко будем
говорить, что объект рождается (излучается) и умирает (поглощается) только на
объекте. Такие элементарные события лежат в основе любых сколь угодно сложных
изменений физического объекта, которые могут фиксировать субъекты. То, что
согласно определению физического объекта, он может быть идентифицирован лишь
относительно и с помощью другого объекта, означает, что это возможно в
результате наблюдения за поведением ни менее чем трех объектов ![]() ,
, ![]() и
и ![]() при двух указанных простейших
изменениях. В результате таких изменений объект
при двух указанных простейших
изменениях. В результате таких изменений объект![]() , называемый сигналом,
должен рождаться на каком-нибудь объекте пары {
, называемый сигналом,
должен рождаться на каком-нибудь объекте пары {![]() ,
,![]() } и умирать на другом объекте этой пары. Естественно,
что рождение и смерть сигнала должны
предшествовать друг другу, в соответствии с принятым выше положением о существовании
предшествования любых двух объектов (состояний, событий и т.п.). Можно даже
сказать, что существование такого предшествования эквивалентно самому существованию
физических объектов (возможности наблюдения за ними), или, как говорят математики,
- тому, что характеристики их имеют конечные значения. Фиксировать эти события
субъект может или непосредственно (с помощью своих органов чувств: зрения,
слуха, осязания, обоняния и т.п. - некоторые люди утверждают, что они обладают
нечувственным восприятием), или опосредствовано - с помощью, например, приборов
или других субъектов. В любых случаях не должны вноситься существенные
искажения в наблюдение (в крайнем случае, должна существовать возможность
учитывать их), о наличии которых можно судить лишь по величине разброса
результатов неоднократно проводимых наблюдений в сходных условиях.
} и умирать на другом объекте этой пары. Естественно,
что рождение и смерть сигнала должны
предшествовать друг другу, в соответствии с принятым выше положением о существовании
предшествования любых двух объектов (состояний, событий и т.п.). Можно даже
сказать, что существование такого предшествования эквивалентно самому существованию
физических объектов (возможности наблюдения за ними), или, как говорят математики,
- тому, что характеристики их имеют конечные значения. Фиксировать эти события
субъект может или непосредственно (с помощью своих органов чувств: зрения,
слуха, осязания, обоняния и т.п. - некоторые люди утверждают, что они обладают
нечувственным восприятием), или опосредствовано - с помощью, например, приборов
или других субъектов. В любых случаях не должны вноситься существенные
искажения в наблюдение (в крайнем случае, должна существовать возможность
учитывать их), о наличии которых можно судить лишь по величине разброса
результатов неоднократно проводимых наблюдений в сходных условиях.
Существование
определенных разбросов неизбежно, поскольку как объекты, так и субъекты
являются вероятностными системами, о чем уже говорилось выше. Известные
трудности определения и учета таких разбросов при наблюдениях микро и мегаобъектов
связаны с существованием двух выше упомянутых экстремумов, ограничивающих возможность
установить предшествование в случаях слишком малых или слишком больших
значениях их. Эти два предельных случая формально можно рассматривать как, своего
рода, границы, по мере приближения к которым уменьшается возможность разделять
объекты и субъекты. В непосредственной близости от этих границ практически невозможно
определить, способны ли субъекты идентифицировать объекты (с помощью сигнала) полностью
самостоятельно или для этого принципиально необходимо использовать еще и нечто
дополнительное, например, сложную аппаратуру. Другими словами, невозможно определить,
где заканчивается субъект и начинается объект, который надо идентифицировать,
т.е. куда нужно относить используемую аппаратуру – к объекту или к субъекту.
Тем самым, становится неясным как
определять и какой смысл необходимо/возможно вкладывать в этом случае в понятия
объекты и субъекты. Но это чисто терминологическая проблема и она не влияет
принципиальным образом на возможности дифференцировать объекты и субъекты. Представляется,
что описанный способ наблюдения, называемый в астрономии радиолокацией, где он
наиболее широко используется в явном виде, является универсальным методом, как
в науке, так и в быту, и не только при визуальных наблюдениях.
Понятно,
что элементарное наблюдение является процессом, поскольку в этом случае речь
идет о трех разных объектах ![]() ,
, ![]() и
и ![]() , в то время как сами события рождения и смерти сигнала
, в то время как сами события рождения и смерти сигнала ![]() являются процедурами.
Для математических объектов указанное наблюдение за ними не возможно, в силу
того, что такие объекты несоставные и для них не существует событий рождения и
смерти их. Это эквивалентно тому, что у математических объектов некоторые характеристики,
существующие у физических объектов (например, – материальные и временные),
отсутствуют, т.е. имеют бесконечные значения, о чем подробнее говориться в
конце брошюры.Для объективности наблюдения, т.е. не зависимости его от субъектов
при выборе сигнала, необходимо всегда принимать сигнал универсальным, позволяющим
всем субъектам и во всех случаях определять значения удаленности пар любых
наблюдаемых объектов, включая объекты с минимально и максимально допустимыми
(природой) значениями их. Далее будут сформулированы требования к
универсальному сигналу, существование и использование которого ниже всегда
предполагается, и указан реальный объект, который может быть принят в качестве
него для идентификации физических объектов. Постулируя существование и
единственность такого универсального сигнала (единственность значений его
характеристик), постулируется и однозначность определения характеристик
физических объектов, необходимая для корректности аксиоматического построения
физики. Как сказано выше, три фундаментальные характеристики объекта связаны
друг с другом, т.е. изменение одной из них невозможно без изменения двух
других. Поскольку определение таких характеристик не является процессом
(является процедурой), то не существует критерия того, изменение какого из
свойств объекта необходимо считать причиной изменений других свойств, а какое –
следствием. Каждое из свойств объекта может условно считаться или причиной или
следствием, аналогично «яйцу или курице» из известной философской дилеммы.
являются процедурами.
Для математических объектов указанное наблюдение за ними не возможно, в силу
того, что такие объекты несоставные и для них не существует событий рождения и
смерти их. Это эквивалентно тому, что у математических объектов некоторые характеристики,
существующие у физических объектов (например, – материальные и временные),
отсутствуют, т.е. имеют бесконечные значения, о чем подробнее говориться в
конце брошюры.Для объективности наблюдения, т.е. не зависимости его от субъектов
при выборе сигнала, необходимо всегда принимать сигнал универсальным, позволяющим
всем субъектам и во всех случаях определять значения удаленности пар любых
наблюдаемых объектов, включая объекты с минимально и максимально допустимыми
(природой) значениями их. Далее будут сформулированы требования к
универсальному сигналу, существование и использование которого ниже всегда
предполагается, и указан реальный объект, который может быть принят в качестве
него для идентификации физических объектов. Постулируя существование и
единственность такого универсального сигнала (единственность значений его
характеристик), постулируется и однозначность определения характеристик
физических объектов, необходимая для корректности аксиоматического построения
физики. Как сказано выше, три фундаментальные характеристики объекта связаны
друг с другом, т.е. изменение одной из них невозможно без изменения двух
других. Поскольку определение таких характеристик не является процессом
(является процедурой), то не существует критерия того, изменение какого из
свойств объекта необходимо считать причиной изменений других свойств, а какое –
следствием. Каждое из свойств объекта может условно считаться или причиной или
следствием, аналогично «яйцу или курице» из известной философской дилеммы.
При
изменении характеристик объекта должны меняться и соответствующие удаленности
между этим объектом и другими объектами, чем и определяется связь объектов друг
с другом. Для сравнения различных объектов и их удаленностей между собой, т.е.
для определения предшествования их, на практике используют внешние по отношению
к ним объекты, имеющие мало (медленно) изменяемые характеристики. Эти объекты
можно называть субъективными или назначаемыми масштабами, выбирать которые можно с помощью двух обязательно
существующих объективных или абсолютных масштабов. Абсолютными масштабами
являются объекты или системы их, имеющие самые малые или самые большие
характеристики или удаленности, которые природа (существующие технологии) позволяет определять субъектам. В силу этого, значения
этих характеристик являются фундаментальными постоянными величинами - мировыми
константами и они связаны с упоминавшимися выше двумя экстремумами,
существование которых обусловлено существованием «горизонта». Таким образом,
наблюдение за двумя физическими объектами осуществляется отдельными
предшествующими друг другу этапами, на которых совершаются циклы «излучение-поглощение»
сигнала. Поскольку фиксировать можно только излучение и только поглощение
сигнала (но не существование его вне связи с этими актами, о чем подробнее
говорится ниже), то наиболее надежно упорядочение этапов реализуется, если излучение
сигнала на предыдущем этапа наблюдения предшествует поглощению этого же сигнала
на следующем этапе. Это означает, что на каждом из циклов «излучение-поглощение»
надо использовать один и тот же сигнал. На различных этапах наблюдения пары
объектов могут иметь различные значения пространственной, временной и
материальной удаленности, что выражают словами о том, что физические объекты могут
существовать и меняться относительно друг друга в пространстве, во времени и
материально.
Благодаря
существованию предшествования этапов наблюдения, они могут быть упорядочены с
помощью ряда натуральных чисел. Подчеркнем, что само понятие натуральных чисел,
являющееся фундаментальным понятием естествознания, возникло и осмысливается
как раз исходя из процессов определения
количества и упорядочения физических объектов и состояний, воспринимаемых как
нечто единое целое. Если считать естествознание не «божьим даром», а плодом
человеческого ума, разработанным для облегчения восприятия всего, что создано
Богом, то необходимо воздать «Богу – богово, а кесарю – кесарево». Весьма
образно это сделал Л. Кронекер (1823 – 1891): «Господь бог создал целые числа, все остальное – дело рук человеческих».
Этим Л. Кронекер хотел, по-видимому, сказать еще и то, что даже такие человеческие
творения, как понятия классической математики, считавшиеся до недавнего времени
фундаментальными и вечными, например, понятия континуума, предела, бесконечно
малой переменной величины и т.п., оказались «смертными», как и сам человек, и не
выдержавшими проверку временем. Вот мнение об этом Г. Вейля: «Мы менее чем когда-либо уверены в
незыблемости наиболее глубоких оснований (логики и) математики. Как у всех и
всего в мире сегодня, у нас есть свой «кризис»... Фундаментом математической
дисциплины может, по-видимому, служить категория натуральных чисел, но не
континуум, как он дан в наглядном созерцании», см. [1] стр. 91 и 135. Таким образом, основы классической
математики к концу XIX и началу XX вв.
оказались в кризисном состоянии, и все большее количество математиков начали
склоняться к мысли о необходимости пересмотра фундаментальных понятий
математики и, как следствие, - понятий естествознания. В качестве альтернативы
теоретико-множественному подходу классической математики в начале XX века была разработана нидерландским
математиком Л. Э. Я. Брауэром (1881 –
1966) и его последователями оригинальная программа построения математики,
известная ныне под названием интуиционизм. Основные положения и библиография по
этому вопросу можно найти в известной монографии А. Гейтинга, см. [19], внесшего существенный
вклад в развитие этого направления. Интуиционистскую математику Л. Брауэра
можно считать первой систематической попыткой построения математики на конструктивной
основе. К этому направлению примыкает и так называемый нестандартный анализ. В
советской школе математики аналогичное направление, которое развивал А.А.
Марков и его ученики, было более известно под названием конструктивная
математика, см. [20]. Предметом изучения
такой математики являются конструктивные процессы и соответствующие им конструктивные
объекты, под которыми понимают то, что не может быть расчленено на части при
выполнении таких конструктивных процессов. Представляется, что и физике пора
последовать примеру математики и отказаться от таких своих традиционных нефизических
понятий как «пространственно-временной континуум», «поля», «взаимодействия»,
«системы отсчета» и др. (изменить содержание этих понятий), и пытаться строить
физику аксиоматически. При этом, как это имело место в прошлом на протяжении
всего процесса становления физики, необходимо использовать опыт, накопленный математиками.
Как заметил однажды Давид Гильберт, физика слишком важна, чтобы оставлять ее
физикам.
Т.к.
с момента начала и до окончания каждого этапа наблюдения за объектами сигнал не
фиксируется, а, следовательно, и сами объекты не наблюдаются, то естественно
принимать, что в этом интервале они не меняются, т.е. характеристики объектов
сохраняют свои значения. Это соответствует указанному во Введении «основному принципу теории познания» и,
в частности, взглядам Г. Лейбница (1646 – 1716), который говорил: «Движение имеется лишь там, где происходит
доступное наблюдению изменение; там же, где изменение нельзя установить путем
наблюдения, там нет и никакого изменения», см. [21]. Поэтому любые наблюдаемые изменения объектов (их характеристик),
которые могут быть зафиксированы только по завершении соответствующих этапов,
возможны не менее чем на конечные значения, называемые квантами. Квантами называют и сами объекты-сигналы, изменяющие
состояние наблюдаемой системы объектов при рождении и смерти сигналов-квантов.
Следовательно, любое значение какой-либо характеристики объекта (количественное
значение этой величины), ниже обозначаемой ![]() , можно определять счетным числом ее квантовых изменений или
квантов, составляющих этот объект. Отношение значения величины
, можно определять счетным числом ее квантовых изменений или
квантов, составляющих этот объект. Отношение значения величины ![]() к своему кванту, обозначаемому
к своему кванту, обозначаемому
![]() , будем называть разрешающей способностью этой величины или мерой разрешения (значения) ее, и
обозначать
, будем называть разрешающей способностью этой величины или мерой разрешения (значения) ее, и
обозначать ![]() . Можно, говорить, что
мера указывает во сколько раз величина больше своего кванта. Поскольку
. Можно, говорить, что
мера указывает во сколько раз величина больше своего кванта. Поскольку ![]() , то для численных значений меры имеют место следующие
ограничения
, то для численных значений меры имеют место следующие
ограничения ![]() . С учетом изложенного, целесообразно сопоставлять друг с
другом разные значения одной величины, и даже значения разных величин путем
сравнения их мер. Такое сравнение имеет больший физический смысл и, как можно
увидеть из ниже изложенного, оно более информативно.
. С учетом изложенного, целесообразно сопоставлять друг с
другом разные значения одной величины, и даже значения разных величин путем
сравнения их мер. Такое сравнение имеет больший физический смысл и, как можно
увидеть из ниже изложенного, оно более информативно.
6. Непрерывность наблюдения
и скорость изменения объектов
Под непрерывным наблюдением величины ![]() в каком-либо диапазоне
её значений
в каком-либо диапазоне
её значений ![]() будем понимать такое
наблюдение, при котором фиксируются значения величины последовательно на всех
соседних этапах наблюдения. Под соседними этапами наблюдения за одной и той же
величиной понимаются такие два этапа (при этом один из них предшествует
другому), для которых не существует
иного этапа наблюдения за этой же величиной, предшествующего одному из них и
которому предшествует другой из этих этапов. Если такой этап существует, то он
является соседним к каждому из этих двух этапов. Значения величины определенные
на соседних этапах называются соседними значениями, а изменение величины на таких
этапах будем называть непрерывным
изменением ее. Если некоторые соседние значения величины по тем или иным
причинам не фиксируются (не фиксируются значения достоверно известные как
соседние), то такое наблюдение ее будем считать дискретным. Две величины
будем понимать такое
наблюдение, при котором фиксируются значения величины последовательно на всех
соседних этапах наблюдения. Под соседними этапами наблюдения за одной и той же
величиной понимаются такие два этапа (при этом один из них предшествует
другому), для которых не существует
иного этапа наблюдения за этой же величиной, предшествующего одному из них и
которому предшествует другой из этих этапов. Если такой этап существует, то он
является соседним к каждому из этих двух этапов. Значения величины определенные
на соседних этапах называются соседними значениями, а изменение величины на таких
этапах будем называть непрерывным
изменением ее. Если некоторые соседние значения величины по тем или иным
причинам не фиксируются (не фиксируются значения достоверно известные как
соседние), то такое наблюдение ее будем считать дискретным. Две величины ![]() и
и ![]() будем считать зависящими друг от друга, если между ними
имеется причинно-следственная связь, что означает, кроме всего прочего,
поочередное изменение их. В математике говорят, что эти величины связаны функциональной
связью друг с другом или функционально зависимы. Одну из этих величин
будем считать зависящими друг от друга, если между ними
имеется причинно-следственная связь, что означает, кроме всего прочего,
поочередное изменение их. В математике говорят, что эти величины связаны функциональной
связью друг с другом или функционально зависимы. Одну из этих величин![]() , являющуюся следствием, называют функцией, а другую
, являющуюся следствием, называют функцией, а другую ![]() , являющуюся причиной, – аргументом
и обозначают
, являющуюся причиной, – аргументом
и обозначают![]() . Таким образом, смысл понятия функциональной зависимости в
математике однозначно определен существованием причинно-следственной связи в
физике. Можно сказать, что математика специально создана субъектами для
упрощения восприятия естествознания, и она является неотъемлемой частью его.
Связь между величинами будем считать непрерывной, если вследствие непрерывного
изменения одной величины имеет место непрерывное изменение связанных с ней
величин. Отношение квантов соседних значений
. Таким образом, смысл понятия функциональной зависимости в
математике однозначно определен существованием причинно-следственной связи в
физике. Можно сказать, что математика специально создана субъектами для
упрощения восприятия естествознания, и она является неотъемлемой частью его.
Связь между величинами будем считать непрерывной, если вследствие непрерывного
изменения одной величины имеет место непрерывное изменение связанных с ней
величин. Отношение квантов соседних значений ![]() и
и ![]() двух связанных функциональной
зависимостью величин назовем производной или скоростью изменения соответствующей величины
двух связанных функциональной
зависимостью величин назовем производной или скоростью изменения соответствующей величины ![]() по величине
по величине ![]() . При этом, величина
. При этом, величина ![]() должна быть причиной
(аргументом) следствия (функции)
должна быть причиной
(аргументом) следствия (функции) ![]() . Это отношение квантов обозначается:
. Это отношение квантов обозначается:
![]() (2)
(2)
Определение
производной назовем дифференцированием, а
обратный (симметричный) алгоритм, т.е. алгоритм восстановления значений
величины в каком-то диапазоне изменения ее ![]() по производной, назовем
интегрированием и обозначим
по производной, назовем
интегрированием и обозначим ![]() . Симметричность этих двух алгоритмов состоит в том, что они
взаимно обратимы, т.е. имеют место равенства:
. Симметричность этих двух алгоритмов состоит в том, что они
взаимно обратимы, т.е. имеют место равенства:
![]() , (3)
, (3)
где ![]() – значение величины
– значение величины ![]() в начале указанного
диапазона, в котором необходимо выполнить интегрирование. Это значение надо
прибавлять к результату интегрирования в этом диапазоне, для того чтобы получить
значение величины
в начале указанного
диапазона, в котором необходимо выполнить интегрирование. Это значение надо
прибавлять к результату интегрирования в этом диапазоне, для того чтобы получить
значение величины ![]() в конце диапазона,
т.к. само интегрирование дает лишь приращение величины на этом диапазоне. Отметим,
что в частном случае связи величин
в конце диапазона,
т.к. само интегрирование дает лишь приращение величины на этом диапазоне. Отметим,
что в частном случае связи величин ![]() и
и ![]() , когда при любых значениях
, когда при любых значениях ![]() величина
величина ![]() сохраняет свое
значение –
сохраняет свое
значение – ![]() , производная такой величины формально не существует, т.е.
нельзя выполнить дифференцирование. У постоянной величины нет составляющих её
квантов, т.к. она сама один квант, и производная должна равняться нулю,
впрочем, как и интегрирование нулевых значений. Именно поэтому, в левой части
(3) записано
, производная такой величины формально не существует, т.е.
нельзя выполнить дифференцирование. У постоянной величины нет составляющих её
квантов, т.к. она сама один квант, и производная должна равняться нулю,
впрочем, как и интегрирование нулевых значений. Именно поэтому, в левой части
(3) записано![]() – начальное значение,
сохраняемое постоянной величиной, для которой и имеют место соотношения:
– начальное значение,
сохраняемое постоянной величиной, для которой и имеют место соотношения:
![]() и
и ![]() , т.к.
, т.к. ![]()
Понятно,
что если функцию умножить на постоянную величину, то производная такой функции
будет равна произведению этой постоянной на производную исходной функции. Если
функция представляет собой произведение двух и более функций, то для
дифференцирования такого произведения надо последовательно допускать, что все
сомножители кроме одного являются постоянными величинами, и каждый раз находить
производную такой функции. А результатом дифференцирования исходной функции
будет сумма всех этих операций. Если функция представляет собой сумму двух и
более функций одной и той же переменной, то результатом дифференцирования будет
сумма дифференцирования каждого слагаемого. Таким образом, можно сказать, что
процедура дифференцирования является линейной (первого порядка) и имеют место
следующие соотношения.
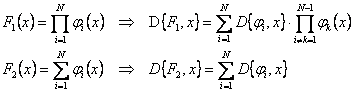 (4)
(4)
Как
указывалось выше, в зависимости от практической возможности или необходимости у
субъекта им может быть установлена различная степень (порядок) предшествования друг
другу состояний объектов. Применительно к квантам - это эквивалентно тому, что
величины их можно в указанных случаях считать состоящими из своих квантов, а
последние – из своих и т.д. Понятно, что в этих случаях алгоритмы (2) и (3)
можно применять соответствующее число раз. При этом можно говорить, что для
величины ![]() можно выполнить
n-кратные дифференцирование и интегрирование. Обозначения их имеют вид:
можно выполнить
n-кратные дифференцирование и интегрирование. Обозначения их имеют вид:
![]() ;
;
![]() .
.
Ниже
для некоторых простейших элементарных функций ![]() , указанных в левой колонке, приведены соотношения между
мерами разрешения входящих в них величин
, указанных в левой колонке, приведены соотношения между
мерами разрешения входящих в них величин ![]() и
и ![]() , а также производные
, а также производные ![]() и интегралы
и интегралы ![]() этих функций (соответственно
вторая, третья и четвертая колонки).
этих функций (соответственно
вторая, третья и четвертая колонки).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если
учесть выше приведенное определение меры
разрешения величины, то выражения для производных функций (третья колонка) получаются
из соотношений между такими мерами входящих в них величин (вторая колонка) в
результате простейших арифметических операций. Выражения для интегралов (четвертая
колонка) находятся в результате выполнения операций обратных операциям
дифференцирования, в соответствии с принятым определением понятия интеграл, см.
(3). Правильность последних соотношений легко может быть проверена путем
дифференцирования их с использованием выше
приведенных формул для определения производных сложных функций, см. (4). Аналогично
можно получать формулы дифференцирования и интегрирования и для иных
функциональных зависимостей величин. Таким образом, можно, оставаясь в рамках арифметических
операций, получать известные из классической математики формулы
дифференцирования и интегрирования функций. Там все такие формулы получены с использованием
довольно непростых для осмысливания понятий бесконечно малая переменная
величина и предел функций.
Обобщим
формулу (3) на случай n-кратных итераций, т.е. выполним n-кратные интегрирования
в диапазоне ![]() n-кратно продифференцированную функцию
n-кратно продифференцированную функцию![]() . Для этого на каждой итерации необходимо использовать
соотношение (3), а также выше приведенные соотношения лишь для степенной
функции. В результате получим следующее выражение, называемое формулой Тейлора:
. Для этого на каждой итерации необходимо использовать
соотношение (3), а также выше приведенные соотношения лишь для степенной
функции. В результате получим следующее выражение, называемое формулой Тейлора:
![]()
![]()
![]()
![]()
![]()
![]() (5)
(5)
Правая
часть этого равенства представляет собой сумму двух частей. Первая из этих частей
называется многочленом Тейлора степени ![]() для функции
для функции![]() . Это приближенное значение функции, определяемое значениями
производных ее в начале диапазона, самим диапазоном и принятым порядком
дифференцирования и последующего интегрирования данной функции. Вторую часть
называют остаточным членом такого ряда. Чем выше принятый порядок
дифференцирования и последующего интегрирования, тем точнее приближенное
значение и тем меньше остаточный член. В частности, если порядок
. Это приближенное значение функции, определяемое значениями
производных ее в начале диапазона, самим диапазоном и принятым порядком
дифференцирования и последующего интегрирования данной функции. Вторую часть
называют остаточным членом такого ряда. Чем выше принятый порядок
дифференцирования и последующего интегрирования, тем точнее приближенное
значение и тем меньше остаточный член. В частности, если порядок ![]() равен максимально
возможному для функции
равен максимально
возможному для функции![]() , то вторая часть равна нулю. Это означает, что данная
функция может быть представлена степенным многочленом порядка
, то вторая часть равна нулю. Это означает, что данная
функция может быть представлена степенным многочленом порядка ![]() . При самой низкой кратности
. При самой низкой кратности
![]() = 1 точность приближенного значения самая низкая, и значение
не меняется с изменением
= 1 точность приближенного значения самая низкая, и значение
не меняется с изменением ![]() . Т.е. приближенное значение совпадает со значением, которое
имела функция в начале диапазона интегрирования. Формулу (5) можно
интерпретировать как процедуру, позволяющую осмысливать и определять (уточнять)
аналитическую связь между собой двух величин. Эта процедура представляет собой
(по аналогии с формулой (5)) предварительное дифференцирование, а затем соответствующее
число раз интегрирование этой связи. В практическом естествознании поступают
аналогичным образом, если хотят более точно идентифицировать какой-то объект или
понятие – определить его свойства. Для этого вначале стараются как можно
детальнее «расчленить» это на составляющие его части, а затем – «сочленить»
(синтезировать) эти части в единое целое. Как уже отмечалось, в этом и состоял
философский метод Декарта. Повторим также, что степень детализации определяется
субъектом в зависимости от его возможности или необходимости идентифицировать
исходный объект.
. Т.е. приближенное значение совпадает со значением, которое
имела функция в начале диапазона интегрирования. Формулу (5) можно
интерпретировать как процедуру, позволяющую осмысливать и определять (уточнять)
аналитическую связь между собой двух величин. Эта процедура представляет собой
(по аналогии с формулой (5)) предварительное дифференцирование, а затем соответствующее
число раз интегрирование этой связи. В практическом естествознании поступают
аналогичным образом, если хотят более точно идентифицировать какой-то объект или
понятие – определить его свойства. Для этого вначале стараются как можно
детальнее «расчленить» это на составляющие его части, а затем – «сочленить»
(синтезировать) эти части в единое целое. Как уже отмечалось, в этом и состоял
философский метод Декарта. Повторим также, что степень детализации определяется
субъектом в зависимости от его возможности или необходимости идентифицировать
исходный объект.
7. Сохранение возможности
движения и связь кинематических параметров объектов с взаимной удаленностью их
Будем
говорить, как уже отмечалось выше, что объекты изменяются пространственным,
временным и материальным образом друг относительно друга, если изменяются соответствующие
характеристики самих объектов а, следовательно, и удаленности их друг от друга.
Количественно изменение объектов определяется значениями производных, связанных
между собой характеристик объектов. Эти производные согласно (2) представляют
собой отношения квантов величин этих характеристик, а квантами являются
разности соседних значений характеристик, определяемые при непрерывном
наблюдении за объектами. Поскольку, как известно из ранее указанного, пространственная,
временная и материальная характеристики объектов связаны между собой, то в качестве
независимой переменной можно принимать любую из них. В соответствии с
традицией, примем независимой переменной временную характеристику – ![]() . Тем самым, любые изменения физических объектов и их взаимной
удаленности, будем считать обязательно происходящими, прежде всего во времени.
Исходя из этого, можно осмыслить и формализовать понятия «прошлое», «настоящее» и «будущее». Будем называть одно из двух
состояний системы прошлым, настоящим или будущим относительно другого состояния
в зависимости от предшествования их временных характеристик. Состояние, временная
характеристика которого предшествует (в соответствии с выбранным «направлением»
между этими двумя состояниями) временной характеристике другого состояния, называется
прошлым, а состояние, которому предшествует какое-то состояние, называется
будущим относительно друг друга. Если указанное предшествование невозможно
установить, что эквивалентно отсутствию его, то оба состояния будем называть
настоящими или одновременными друг относительно друга. Понятно, что если
какое-то состояние является прошлым/настоящим/будущим относительно
какого-нибудь другого состояния, которое в свою очередь является прошлым/настоящим/будущим
относительно третьего состояния, то оба первых два состояния являются
прошлыми/настоящим/будущим относительно этого третьего состояния. Пользуясь
этим положением, можно установить предшествование во времени любых физических
состояний одной и той же системы объектов и различных, но смежных систем
физических объектов, т.е. таких которые имеют один и более общих объектов.
. Тем самым, любые изменения физических объектов и их взаимной
удаленности, будем считать обязательно происходящими, прежде всего во времени.
Исходя из этого, можно осмыслить и формализовать понятия «прошлое», «настоящее» и «будущее». Будем называть одно из двух
состояний системы прошлым, настоящим или будущим относительно другого состояния
в зависимости от предшествования их временных характеристик. Состояние, временная
характеристика которого предшествует (в соответствии с выбранным «направлением»
между этими двумя состояниями) временной характеристике другого состояния, называется
прошлым, а состояние, которому предшествует какое-то состояние, называется
будущим относительно друг друга. Если указанное предшествование невозможно
установить, что эквивалентно отсутствию его, то оба состояния будем называть
настоящими или одновременными друг относительно друга. Понятно, что если
какое-то состояние является прошлым/настоящим/будущим относительно
какого-нибудь другого состояния, которое в свою очередь является прошлым/настоящим/будущим
относительно третьего состояния, то оба первых два состояния являются
прошлыми/настоящим/будущим относительно этого третьего состояния. Пользуясь
этим положением, можно установить предшествование во времени любых физических
состояний одной и той же системы объектов и различных, но смежных систем
физических объектов, т.е. таких которые имеют один и более общих объектов.
Как
видно, здесь имеет место аналогия с ранее определенным понятием
причинно-следственной связи между двумя физическими состояниями или с математическим
понятием функциональной связи между двумя величинами. Принципиально подчеркнуть
то, что сформулированные понятия прошлое, настоящее и будущее являются
субъективными, т.к. должны определяться субъектом в каждом конкретном случае
как процесс и всегда лишь для двух определенных состояний системы. Гносеология
такого субъективизма связана в своей основе с исходным субъективизмом, имевшим
место при определении понятия объект (явление, событие, процесс и т.п.) как того,
что субъект может идентифицировать относительно других объектов. Напомним, что
в традиционной физике объект и все эти понятия, а также понятия прошлое,
настоящее и будущее, не связывают непосредственно с субъектом. Эти определения
является процедурой применимой сразу ко всем объектам рассматриваемой инерциальной
системы отсчета (а не процессом между конкретными объектами), поскольку в такой
системе отсчета постулируется единый пространственно-временной континуум, например,
см. [3]. Временные соотношения между состояниями системы большого числа
объектов, позволяющие относить такие состояний к прошлому настоящему и
будущему, определяются при традиционном подходе исходя из степени так
называемой «упорядоченности/хаотичности» поведения объектов этой системы.
Руководствуются при этом «вторым началом термодинамики», которое утверждает,
что состояние «изолированной» системы является прошлым относительно другого
состояния этой системы, если оно более «упорядочено», т.е. с течением времени
состояния таких систем становятся более «хаотичными». Вопреки общепринятому мнению
о том, что такое отнесение состояний во времени считается объективным, строго
говоря, оно таковым не является, поскольку само понятие «упорядоченности/хаотичности»
поведения объектов является субъективным и во многом интуитивным понятием.
Состояние считающиеся «хаотичным» для одного субъекта может считаться
«упорядоченным» для другого субъекта или
даже для одного и того же субъекта на разных этапах познания этого состояния.
Примером могут служить письменность или речь иностранца, пока они не изучены, не
говоря уже о различных криптограммах и шифрованных сообщений, код которых еще
не раскрыт. Такую же субъективность можно отнести и к проявлению случайности, которую,
строго говоря, можно считать таковой, пока не удастся установить
«закономерность этой случайности».
Таким образом,
абсолютно объективное отнесение двух состояний к прошлому, настоящему или
будущему друг относительно друга, не возможно. Но практически состояние
считается прошлым, настоящим или будущим, если одна из этих трех возможностей
признается имеющей место подавляющим большинством субъектов. По аналогии с фактически
признаваемыми большинством людей, следующими определениями красоты,
порядочности, интеллигентности, душевности и т.п.: «красивым и т.п. называют
то, что большинство таковым считает». И хотя на различных этапах развития
общества мнение большинства может меняться, принятое упорядочение состояний, а
также указанные определения могут считаться на каждом из таких исторических
этапов объективными, поскольку они не зависят от мнения одного или даже небольшого
числа субъектов. Аналогичная ситуация имеет место и в отношении того, что
считать истиной. Истинность определяется конкретными субъектами, а
объективность истины обеспечивается только количеством (подавляющим большинством)
субъектов согласных с такой оценкой, поскольку мнения одного или даже
небольшого числа субъектов, отличающиеся от мнения большинства, не могут изменить соотношение между
большинством и меньшинством. Это же положение лежит и в основе демократии
известной человечеству с момента его возникновения, и до сих пор являющейся
самой прогрессивной формой народовластия, принятой большинством цивилизованных
стран. Принципы демократии распространяется как на выбор внутриполитического
устройства таких стран (выборность органов власти, плебисциты и т.п.), так и на
другие системы организации общества. Например, на судебную систему (институт
присяжных заседателей), на систему
оценки спортивных достижений (если не используются специальные приборы),
на многое другое и даже на оценку творчество ученых (публичная защита
диссертаций) и деятелей искусства. Можно сказать, что это есть одно из
проявлений закона перехода количества в качество, поскольку существование
какого-то качества у объекта или понятия определяется количеством (большинством)
субъектов признающих это. Изложенное еще раз убеждает в том, что понятие время
во многом является субъективным понятием, но никак не абсолютно объективным,
как это считается в традиционной физике. Прав был русский философ П.Я. Чаадаев,
говоривший, что «Все времена мы создаем
сами, в этом нет сомнения, бог времени не создал, он дозволил его создать
человеку», см. [24] стр. 621. И, исходя из
такого «дозволения», у различных людей и даже сообществ в силу их разнообразия восприятие
времени различно, и даже существенно отличается от принятого в традиционной физике. Так
существуют народности (племена) не знакомые с восприятием времени в традиционной
физике, которые в своей повседневной жизни обходятся принципиально иным
осмысливанием продолжительности и последовательности событий. Вот что по этому
поводу пишет в своей книге «Парадоксы науки» А. Сухотин, см. [27]: «Европейские языки, например, имеют два
больших класса слов: существительные и глаголы. Соответственно это вещи и
процессы. Однако в некоторых языках,
например у индейцев нутка, все слова соотносимы с нашими глаголами, то есть
выражают действие. Скажем, понятие «волна» или «молния» у нас – существительные
и обозначают вещи, а у нутка – глаголы. Они выражают движение и процессы.
Сообразно этому люди нутка видят и окружающую действительность.
Или же, развивает свою гипотезу
Б. Уорф, есть языки, в которых отсутствует категория времени. Так, у
индейцев хопи (США) нет временных понятий. В частности, они не говорят «пять
дней». Хопи скажет: «Я был на охоте до шестого дня», или: «Я вернулся с охоты
после пятого дня». Иначе сказать, в этом языке не используется выражение
длительности. Вместо нее просто отмечают начало или конец чего-либо, не само
временное протекание процесса, а его границы».
Предлагаемый подход тоже не использует введенное
еще Ньютоном традиционное понятие «длительность», а исходит из понятия предшествования
друг другу конкретных объектов (событий, явлений, процесс и т.п.). В такой же
степени субъективным, как и время является принятое в предлагаемом подходе и иначе
осмысливаемое понятие пространства (пространственно-временного континуума).
Обобщая, можно сказать, что субъективным является и само естествознание, о чем
уже говорилось ранее, поскольку оно создается и может изменяться субъектами
исходя из своих возможностей и по мере появления необходимости.
Изменение
пространственной удаленности между объектами (расстояния между ними) называется
относительным движением их. Можно
сказать, что согласно выше приведенным определениям понятий объекты имеет место
закон сохранения возможности движения,
в соответствии с которым, для любого
объекта всегда существуют такие другие объекты (по крайней мере, существует
один), относительно которых возможно движение этого объекта. Действительно,
абсолютное отсутствие изменений (движений) объекта относительно каких либо
других объектов означает невозможность наблюдения за ним, что эквивалентно
отсутствию самого этого объекта. Ясно, что в силу функций выполняемых сигналом,
отсутствует возможность фиксировать относительное движение двух объектов, одним
из которых является сигнал. Это связано с тем, что определять изменение расстояния
а, следовательно, наблюдать относительное движение можно лишь с помощью сигнала
и, следовательно, только для пар объектов, ни один из которых не является
сигналом. Поскольку фиксировать можно лишь рождение и смерть сигнала, но не сам
сигнал вне связи с этими событиями, то понятие движения сигнала и скорость его,
могут быть введены только относительно двух других объектов, на которых он
рождается, и умирает. Формально можно считать, что при рождении и при смерти сигнала он
пространственно удален соответственно от объекта смерти и от объекта рождения
на величину пространственной удаленности этих двух объектов друг от друга. Эта
удаленность не может состоять из частей, определяемых в результате отдельных
актов наблюдения. Она определяется одним элементарным этапом наблюдения, состоящим
из двух простейших событий – рождения и смерти сигнала.
Поэтому,
квант пространственной удаленности сигнала ![]() от каждого из объектов
от каждого из объектов
![]() и
и ![]() при таких двух
событиях будет совпадать с самой пространственной удаленностью его от каждого
из этих объектов, являющейся пространственной удаленностью объектов друг от
друга. Очевидно, что такому кванту пространственной удаленности сигнала
соответствует квант временной удаленности его от каждого из этих объектов,
совпадающий с временной удаленностью объектов друг относительно друга. Это
означает, что понятие квант временной удаленности двух объектов эквивалентно
понятию интервал наблюдения. Поэтому скорость движения сигнала между объектами
при таких двух
событиях будет совпадать с самой пространственной удаленностью его от каждого
из этих объектов, являющейся пространственной удаленностью объектов друг от
друга. Очевидно, что такому кванту пространственной удаленности сигнала
соответствует квант временной удаленности его от каждого из этих объектов,
совпадающий с временной удаленностью объектов друг относительно друга. Это
означает, что понятие квант временной удаленности двух объектов эквивалентно
понятию интервал наблюдения. Поэтому скорость движения сигнала между объектами ![]() и
и ![]() , определяемая отношением
кванта пространственной удаленности к кванту временной удаленности, равна
отношению пространственной удаленности этих объектов –
, определяемая отношением
кванта пространственной удаленности к кванту временной удаленности, равна
отношению пространственной удаленности этих объектов –![]() к временной удаленности их –
к временной удаленности их –![]() . Ясно, что такая скорость,
обозначаемая ниже
. Ясно, что такая скорость,
обозначаемая ниже ![]() , должна быть наибольшей из относительных скоростей
движения любых наблюдаемых объектов. Иначе с помощью сигнала нельзя будет
наблюдать объекты, относительная скорость которых больше его скорости, и такой
сигнал нельзя считать универсальным. Следовательно, скорость универсального сигнала
постоянна, и она является фундаментальной константой. Исходя из этого,
формально можно считать, что сигнал в промежутке между своим рождением и
смертью находится на прямой, определяемой двумя наблюдаемыми объектами, и
располагается между ними («предшествует» лишь одному из них). Согласно
изложенного, интервал элементарного наблюдения –
, должна быть наибольшей из относительных скоростей
движения любых наблюдаемых объектов. Иначе с помощью сигнала нельзя будет
наблюдать объекты, относительная скорость которых больше его скорости, и такой
сигнал нельзя считать универсальным. Следовательно, скорость универсального сигнала
постоянна, и она является фундаментальной константой. Исходя из этого,
формально можно считать, что сигнал в промежутке между своим рождением и
смертью находится на прямой, определяемой двумя наблюдаемыми объектами, и
располагается между ними («предшествует» лишь одному из них). Согласно
изложенного, интервал элементарного наблюдения – ![]() за двумя объектами
может быть выражен через расстояние между ними
за двумя объектами
может быть выражен через расстояние между ними![]() и скорость сигнала
и скорость сигнала ![]() следующим образом:
следующим образом:
![]() (6)
(6)
Ниже
более подробно обсуждается лишь вопрос об изменении пространственной
удаленности объектов как функции времени – их относительном движении, т.к. это
представляется ключевой проблемой физики и естествознания в целом. Аналогично
могут быть прослежены вопросы изменения и других пар фундаментальных
характеристик объектов, связанных, как указывалось выше, между собой. С учетом
(6), наблюдаемая скорость изменения по времени расстояния ![]() между двумя объектами
между двумя объектами ![]() и
и ![]() , определяемая согласно (2), будет обратно пропорциональна
самому расстоянию:
, определяемая согласно (2), будет обратно пропорциональна
самому расстоянию:
![]() (7)
(7)
В
существовании такой зависимости относительной скорости движущихся объектов от их
взаимной удаленности можно убедиться, наблюдая за проносящимися мимо
автомобилями (любыми другими объектами) визуально или используя приборы,
способные замерять удаленности автомобиля до наблюдателя на каждом этапе
наблюдения. Скорость автомобиля увеличивается по мере приближения его к объекту
(где и находится наблюдатель, фиксирующий скорость автомобиля) и уменьшается по
мере удаления. Принципиальное отличие таких наблюдений от показаний, например,
спидометра, находящегося в салоне автомобиля и предназначенного для определения
скорости движения его внутренним наблюдателем, обусловлено тем, что обычно такой
спидометр показывает скорость автомобиля только относительно находящихся под
ним участков трассы. Чаще всего, спидометр показывает скорость вращения вала
автомобиля, которая может быть неоднозначным образом связана с изменением
расстояния между внешним наблюдателем и автомобилем. В частности, это имеет
место, если автомобиль движется по скользкой или не абсолютно жесткой трассе.
Таким образом, фактическая скорость относительного движения двух объектов должна
определяться по формуле (7) путем определения взаимной удаленности между
объектами, и поэтому такая скорость при прочих постоянных условиях всегда
обратно пропорциональна расстоянию между ними. Описанное в определенной мере
эквивалентно эффекту Доплера, согласно которому удаление/приближение приемника
колебаний к источнику их соответствует уменьшению/увеличению скорости (частоты)
волны. Формально с позиций традиционной физики такая зависимость относительной
скорости двух объектов от расстояния между ними может быть объяснена тем, что
на каждом этапе наблюдения в качестве масштаба, используемого для фиксирования
изменений текущей удаленности двух объектов, принимается расстояния между этими
же объектами, замеренные или в начале или в конце соответствующих этапов. Такой
выбор масштабов представляется наиболее разумным и естественным, т.к. иной
выбор, требует использование других объектов, доступ к которым может
отсутствовать в случае двух объектов находящихся, например, в открытом море или
в космосе. Но даже при наличии этих других объектов необходимо учитывать
движение их относительно двух
рассматриваемых объектов, что может существенно усложнить определение
относительной скорости двух наблюдаемых объектов. Исходя из выше изложенных
соображений, будет иметь место и следующее выражение для кинематических
параметров любого порядка этих объектов:
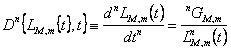 (8)
(8)
Физический
смысл величин ![]() будет раскрыт ниже.
Подчеркнем еще раз, при таком качественном и количественном определении движения
объектов не используются никакие дополнительные понятия, кроме ранее введенных понятий
фундаментальных характеристик физических объектов. Не используются понятие пространственно-временного
континуума, его «кривизны» и другие понятия, существенным образом применяемые
при традиционном построении физики. Например, не используются понятие сил действующих
на объекты, и понятие координат их в какой-либо системе отсчета, существующей
(движущейся или неподвижной) в неподвижном и неизменяемом пространстве и в
абсолютном времени. Последние понятия введены на ранних этапах развития естествознания
исходя из наблюдений за явлениями, ограниченными только земными условиями. При
этом явно или неявно предполагалось существование недеформируемой материальной
среды, иначе называемой эфиром, субстанцией и т.п., частным случаем которой вначале
считалась плоть земли. Введение такой среды представляется искусственным, поскольку
она не всегда используется даже при наблюдениях в земных условиях, не говоря
уже о наблюдениях внеземных. Мы наблюдаем материальные объекты как непосредственно,
так и с помощью приборов, только с использованием и относительно других конечных
(не континуальных) материальных объектов. Поэтому указанные традиционные
понятия не являются необходимыми для познания природы. «В природе мы познаем собственно только движение, без которого чувственное
впечатление невозможно. Все прочие понятия, например геометрические, произведены
нашим умом искусственно, будучи взяты в свойствах движений, а потому
пространство само собой отдельно для нас не существует». Это мнение
геометра - гениального Н. И. Лобачевского (1792 – 1856), создателя неэвклидовой
геометрии, существенно изменившей наши взгляды на естествознание.
будет раскрыт ниже.
Подчеркнем еще раз, при таком качественном и количественном определении движения
объектов не используются никакие дополнительные понятия, кроме ранее введенных понятий
фундаментальных характеристик физических объектов. Не используются понятие пространственно-временного
континуума, его «кривизны» и другие понятия, существенным образом применяемые
при традиционном построении физики. Например, не используются понятие сил действующих
на объекты, и понятие координат их в какой-либо системе отсчета, существующей
(движущейся или неподвижной) в неподвижном и неизменяемом пространстве и в
абсолютном времени. Последние понятия введены на ранних этапах развития естествознания
исходя из наблюдений за явлениями, ограниченными только земными условиями. При
этом явно или неявно предполагалось существование недеформируемой материальной
среды, иначе называемой эфиром, субстанцией и т.п., частным случаем которой вначале
считалась плоть земли. Введение такой среды представляется искусственным, поскольку
она не всегда используется даже при наблюдениях в земных условиях, не говоря
уже о наблюдениях внеземных. Мы наблюдаем материальные объекты как непосредственно,
так и с помощью приборов, только с использованием и относительно других конечных
(не континуальных) материальных объектов. Поэтому указанные традиционные
понятия не являются необходимыми для познания природы. «В природе мы познаем собственно только движение, без которого чувственное
впечатление невозможно. Все прочие понятия, например геометрические, произведены
нашим умом искусственно, будучи взяты в свойствах движений, а потому
пространство само собой отдельно для нас не существует». Это мнение
геометра - гениального Н. И. Лобачевского (1792 – 1856), создателя неэвклидовой
геометрии, существенно изменившей наши взгляды на естествознание.
Имея
выражения для кинематических параметров, можно с помощью (5) или решая
дифференциальные уравнения, в которых используются эти выражения, получать необходимые
приближения для зависимости пространственной удаленности двух объектов от
времени. Как уже указывалось, чем выше порядок кинематических параметров, применяемых
для определения связей величин друг с другом, тем большая точность определения
таких зависимостей. Отсюда ясно, что использование в фундаментальных законах
традиционной физики производных лишь второго порядка от расстояния по времени,
можно рассматривать как второе приближение при описании физической картины
мира. Будем называть его приближением Галилея. Подходы Аристотеля, которыми
довольствовалось человечество на ранних этапах своего развития, и в которых
фигурировала лишь первая производная от расстояния по времени, можно считать
первым приближением. Если следовать Лейбницу, который рассматривал покой как
предельный случай движения, а не противоположность его, то статическое состояние
объектов, которое эквивалентно нулевому порядку производной от расстояния по
времени, можно рассматривать как «нулевое приближение». Совершенно очевидно, и
это указывалось выше, что использование производных более высокого порядка
приведет к более точному и полному описанию картины мира. Учитывая, что
традиционная физика строится как эмпирическая наука, а также то, что
последующие уточнения предыдущих приближений слишком малы, чтобы быть непосредственно
и повсеместно зафиксированными даже современной экспериментальной техникой (иначе
это уже имело бы место), приближения третьего и более высоких порядков пока не
востребованы традиционной физикой. Понятно, что это не исключает возможность и
необходимость использование более высоких приближений в дальнейшем. Можно
сказать с уверенностью, что потребность в таких приближениях появится в
ближайшее время, и они будут востребованы не только теорией при формулировании
фундаментальных законов физики, но и использованы практикой при разработке
новых технологических решений.
Но
уже сейчас имеется одна проблема, полностью решить которую в традиционной
физике ограниченной рамками второго приближения пока не удается, и которая
автоматически решается, если отказаться от традиционного подхода и учесть
приближения более высоких порядков. Имеется в виду одна из самых трудных и
загадочных проблем, носящая название проблема необратимости или проблема «Стрелы
Времени». Последний термин ввел в физику в 1928 г. известный английский физик и
астроном Артур Эддингтон (1882 – 1944). Эту проблему кроме Эддингтона пытались
решить еще и такие светлые умы человечества как знаменитый французский физик и
математик Пьер Симон Лаплас (1749 –1828), австрийский физик Людвиг Больцман
(1844 – 1906), А. Пуанкаре и многие другие ученые. Достаточно подробный и
весьма квалифицированный анализ возникающих при этом сложностей, а также свое
видение решения их, приведен известным бельгийским мыслителем и ученым русского
происхождения И. Р. Пригожиным (1917-2003), см. [16]. В своей лекции по случаю
присуждения ему в 2004 году Нобелевской Премии по физике В.Л. Гинзбург назвал
проблему необратимости первой из «… трех
«великих» проблем современной физики». Суть этой проблемы в одном
принципиальном расхождении между принятыми традиционной физикой
фундаментальными законами естествознания (законами фундаментальных
взаимодействий) и наблюдаемым поведением физических объектов. Для всех реальных
физических процессов и явлений наблюдается необратимость или несимметричность
во времени, заключающаяся в том, что процессы протекают всегда в одном «временном
направлении». При попытках вернуться назад – повторить процесс в обратной
последовательности, система не возвращается в исходное состояние. Поскольку временную
характеристику объекта мы выбрали в
качестве независимой переменной, а все остальные характеристики являются функциями ее, то поэтому говорят,
что для реальных процессов с участием физических объектов время всегда течет
только в одном направлении – от прошлого к будущему. Говоря иначе, для этих
процессов время является индикатором этого единственного направления, т.е. –
индикатором того, какой из двух процессов «прямой» или «обратный» предшествует
друг другу.
С
другой стороны, до сих пор считается, что все фундаментальные закономерности
традиционной физики – аналитический вид их – для отдельных микро и макро
объектов обладают, временной обратимостью или инвариантностью (инвариантностью
относительно знака изменения времени). Временная инвариантность в традиционной
физике обусловлена тем, что в ней ограничиваются вторым приближением. Т.е. тем,
что во все фундаментальные закономерности время входит только в виде второй
производной от физических величин по времени, (что эквивалентно тому, что
дифференциал времени используется только в виде квадрата в знаменателях
выражений). Но если исходить из принятого традиционной физикой положения о том,
что изменение направления (хода) времени не влияет на вид фундаментальных
закономерностей для каждого отдельного объекта, то принятое положение должно
иметь место и для любых наблюдаемых явлений, в которых участвует любое число таких
объектов. Встречающиеся противоположные суждения о том, что только количество
взаимодействующих объектов само по себе (вне связи с характеристиками самих
объектов) может качественно изменить поведение таких систем, должны считаться
голословными до тех пор, пока не будут выявлены физические механизмы таких
изменений. Не смотря на то, что выявить такие механизмы не удается (и, скорее
всего не удастся и в будущем), обратимость для отдельных объектов в
традиционной физике считается справедливой вот уже на протяжении более трех
веков. Это классический и наиболее удивительный (парадоксальный) пример живучести
веры, т.е. пример того, как может превалировать вера над знанием.
Удивительность заключается в том, что в отличие от других примеров, когда
знанию предпочитается вера и когда невозможно опровергнуть (как и подтвердить)
веру, например, веру в загробную жизнь, в данном случае у каждого имеется возможность
убедиться в ошибочности обратимости фундаментальных законов, строгое следование
которым приводит к расхождению с экспериментально наблюдаемыми явлениями.
Как
известно, любая теория, тем более фундаментальная, не может считаться
правильной, если существует, хотя бы одно экспериментально наблюдаемое явление,
противоречащее ей. Но поскольку имеет место противоречие не с одним, а со всеми
наблюдаемыми явлениями, то обратимость на фундаментальном уровне продолжают
считать правильной, руководствуясь при этом алогичным правилом: «если теория не
соответствует фактам, то тем хуже для фактов». Для описания «плохих» явлений,
для которых наблюдается необратимость времени (а она практически наблюдается
для всех явлений), искусственно вводят в
дифференциальные или интегральные уравнения для этих явлений члены, не
обладающие временной инвариантностью,
например, вводят члены с производными по времени нечетного порядка. При этом считают,
что таким способом учитывается влияние других объектов и факторов, не рассматриваемых
в данной задаче, чтобы не усложнять ее, и что эти объекты каким-то образом
создают силы диссипации, действующие на наблюдаемый объект, и тем самым приводят
к необратимости. Тем самым предполагают, что если бы удалось корректно (в
соответствии с обратимыми фундаментальными законами традиционной физики)
рассмотреть влияние всех объектов и факторов, влияющих на рассматриваемое
явление, то необратимость не имела бы место. Другими словами, считают, что в абсолютно
изолированной системе необратимость не имела бы место. Такое объяснение
необратимости представляется искусственным и не способным решить эту проблему принципиальным
образом, т.к. в реальных процессах являющихся необратимыми все влияющие друг на друга
объекты всегда участвуют и влияют друг
на друга вне зависимости от наших возможностей учитывать их такое их взаимное влияние.
К тому же, всегда имеется возможность учесть достаточное число объектов, систему
которых можно рассматривать с любой степенью точности как абсолютно
изолированную. В конце концов, природа в целом является абсолютно изолированной
системой, но тем ни менее необратимость всегда имеет место. Таким образом,
существующее в традиционной физике положение об обратимости времени на фундаментальном
уровне и объяснение фактически наблюдаемой необратимости за счет влияний, не
учитываемых объектов и факторов, является несостоятельным. Внешние объекты
могут влиять на необратимость наблюдаемых систем объектов лишь количественно –
могут увеличивать или уменьшать ее в ограниченном диапазоне, но ни какое внешнее
влияние или отсутствие его не может привести к качественному изменению, т.е. не
может исключить необратимость.
Вместе
с тем, очевидно, что если в соответствии с вышеприведенными возможностями
нетрадиционного подхода к физике использовать приближения более высокие чем
второе, то необратимость времени возникает уже в самих фундаментальных
закономерностях и при этом отпадает необходимость искусственно вводить
какую-либо причину необратимости, обусловленную существованием каких-то, не
учитываемых объектов и факторов. В силу малости поправок, вносимых более
высокими приближениями, заметные проявления необратимости малы в случаях
рассмотрениях малого числа несоставных объектов. Для фиксирования необратимости
в таких системах объектов требуются более тщательные и длительные наблюдения,
чем для систем большого числа составных объектов. Это наглядно проявляется,
например, для систем относительно малого числа наблюдаемых планет, в поведении
которых обнаружить необратимость крайне сложно, и для этого требуются
несравнимо большие временные затраты, чем для систем большого числа объектов
наблюдаемых как в земных условиях, так и в планетарных масштабах. В случаях большого
числа объектов малые поправки для отдельных пар их «резонируют» друг с другом, накапливаются
и увеличиваются и тем самым сокращается время проявления необратимости по
сравнению с единичными парами объектов. Можно сказать, что это одно из
проявлений закона перехода количества в качество. Впервые мысль о том, что
происхождение необратимости времени можно объяснить неточностью фундаментальных
исходных закономерностей, была высказана в 50 годах ХХ столетия известным
советским астрономом Н.А. Козыревым (1908 – 1983). Но тогда эту дерзкую мысль
не удалось ни разработать теоретически, ни тем более обосновать экспериментально.
В последнее время появились аналогичные высказывания о том, что фундаментальные
законы природы могут быть не точны. Вот мнение уже упоминавшегося авторитетнейшего
российского физика лауреата Нобелевской премии В.Я. Гинзбурга: «Так наличие
фундаментальной длины ![]() может привести к изменению зависимости силы
гравитационного притяжения от расстояния между взаимодействующими телами
(частицами и т.д.). Речь идет, конкретно, о том, что Ньютоновский закон для гравитационной
потенциальной энергии
может привести к изменению зависимости силы
гравитационного притяжения от расстояния между взаимодействующими телами
(частицами и т.д.). Речь идет, конкретно, о том, что Ньютоновский закон для гравитационной
потенциальной энергии ![]() при малых
при малых ![]() станет более крутым
(сейчас известно лишь, что закон
станет более крутым
(сейчас известно лишь, что закон ![]() справедлив при
справедлив при ![]() см.). Я убежден, что соответствующее направление исследований
будет в центре внимания в обозримом будущем», см. [15]. Следует заметить, что
подходы к естествознанию, на основании которых сделан прогноз в предыдущей
цитате, отличаются от подходов, излагаемых в данной брошюре, хотя и основаны
они тоже на дискретном характере естествознания. Небезынтересным представляется
мнение А. Пуанкаре, высказанное им о том, почему применение более высоких
приближений для описания физических явлений вызывает отторжение его. «…В конце концов, как из всего этого видно, пришлось
бы заключить, что порядок уравнений, определяющих расстояния, выше второго.
Почему бы это могло смущать нас – почему мы находим вполне естественным, что
ряд явлений зависит от начальных значений первых производных расстояний, и в
тоже время не решаемся допустить, что они могут зависеть от начальных значений
вторых производных? Это может быть только следствием известных
привычек, выработанных в нашем сознании постоянным изучением обобщенного
принципа инерции его следствий» (выделение моё Б.Р.), см. [12], стр.81.
Надеюсь, что читатель согласится с тем, что «привычки» не могут служить
надежным основанием для построения сколько-нибудь серьезной теории, не говоря
уже – о построении теоретической физики, являющейся основой естествознания.
см.). Я убежден, что соответствующее направление исследований
будет в центре внимания в обозримом будущем», см. [15]. Следует заметить, что
подходы к естествознанию, на основании которых сделан прогноз в предыдущей
цитате, отличаются от подходов, излагаемых в данной брошюре, хотя и основаны
они тоже на дискретном характере естествознания. Небезынтересным представляется
мнение А. Пуанкаре, высказанное им о том, почему применение более высоких
приближений для описания физических явлений вызывает отторжение его. «…В конце концов, как из всего этого видно, пришлось
бы заключить, что порядок уравнений, определяющих расстояния, выше второго.
Почему бы это могло смущать нас – почему мы находим вполне естественным, что
ряд явлений зависит от начальных значений первых производных расстояний, и в
тоже время не решаемся допустить, что они могут зависеть от начальных значений
вторых производных? Это может быть только следствием известных
привычек, выработанных в нашем сознании постоянным изучением обобщенного
принципа инерции его следствий» (выделение моё Б.Р.), см. [12], стр.81.
Надеюсь, что читатель согласится с тем, что «привычки» не могут служить
надежным основанием для построения сколько-нибудь серьезной теории, не говоря
уже – о построении теоретической физики, являющейся основой естествознания.
9. Конечные и бесконечные
расстояния – излучение и поглощение
Согласно
(8) при увеличении расстояния между двумя объектами (при прочих равных
условиях, которые, вообще говоря, никогда абсолютно точно не имеют место) относительные скорость, ускорение и другие
кинематические параметры объектов уменьшаются, а при уменьшении расстояния –
увеличиваются. Причем, чем более высокий порядок имеют кинематические
параметры, тем быстрее происходят их изменения. На определенном этапе таких
монотонных изменений пропадает практическая возможность идентифицировать
различные значения, т.е. отличать друг от друга значения, замеренные на
предыдущих и последующих этапах наблюдения. Эти значения кинематических
параметров (сами параметры в таком состоянии) называют неизмеримыми или бесконечными, в отличие от измеримых
или конечных значений, которые можно
отличить друг от друга. Вместе с тем, каждый параметр может изменяться
(наблюдаться) в каком-то диапазоне значений, определяемом наибольшим и
наименьшим величинами выше названными экстремумами. Конечные и бесконечные
значения отличаются от двух таких экстремумов тем, что последние не могут быть
соседними друг с другом, т.е. непосредственно предшествовать друг другу. В то
же время, как конечные, так и бесконечные значения, в силу своих определений,
не могут не быть соседними друг с другом, а иногда и соседними с одним из
экстремумов. Если экстремум не меньше соседних бесконечных значений, то будем
называть его максимум, а соседние
бесконечные значения называются бесконечно
большими. Если экстремум не больше соседних бесконечных значений, то будем
называть его минимум, а соседние
бесконечные значения бесконечно малыми.
Будем говорить, что бесконечные значения (число их в общем случае не
лимитировано) отличаются от соседних значений на не более чем элементарные
(квантовые) величины, а конечные значения отличаются друг от друга на не менее
чем элементарные величины.
Следует
различать случаи, когда каждый из трех рассматриваемых объектов (это минимально
допустимое число объектов, для корректного рассмотрения их) удален от всех
других объектов на конечные и на бесконечные расстояния. В первом из этих
случаев экстремумы взаимной удаленности двух таких объектов будем называть
локальными, а во втором случае – глобальными или фундаментальными. Значения кинематических
параметров до и после локальных экстремумов остаются конечными, а в случаях
глобальных экстремумов конечными остаются лишь значения или до или после них, в
зависимости от того является ли глобальный экстремум соответственно максимумом
или минимумом. В частности, конечные длины сторон треугольника при изменении
его углов принимают значения локальных экстремумов, количественно определяемые
соотношениями (1). Используемые в этих соотношениях коэффициенты – косинусы –
как раз и являются математическими функциями, описывающими локальные
экстремумы. Количество локальных экстремумов зависит от числа объектов,
удаленных от двух рассматриваемых объектов на конечные расстояния, а глобальных
экстремумов существует только два. Можно сказать, что определенные выше
глобальные экстремумы соответствуют так называемым в математике «бесконечным
несобственным» числам +∞ и –∞, присоединяемым к системе
действительных чисел, и таким образом осмысливается понятие «актуальной»
бесконечности, см. [7]. Понятие «потенциальной» бесконечности в определенном
смысле адекватно выше введенным понятиям бесконечных (неизмеримых) величин.
Учитывая
итерационный способ вычисления кинематических параметров более высокого порядка
с использованием параметров предыдущих порядков, если какой-нибудь
кинематический параметр является локальным экстремумом и, благодаря этому
соседние с ним значения неразличимы между собой, то кинематический параметр
следующего более высокого порядка будет отсутствовать – будет равен нулю. Если
этот экстремум является глобальным, то нулю будут равны уже все кинематические
параметры более высокого порядка, а не только следующий. Можно говорить и
наоборот – кинематический параметр, порядок которого предшествует порядкам
нулевых кинематических параметров, достигает своего экстремального значения,
локального или глобального в зависимости от числа равных нулю кинематических
параметров более высокого порядка.
Заметим, что сами понятия «конечные», «бесконечные» и «экстремальные» являются
объективными понятиями, не смотря на субъективный характер любых количественных
значений таких величин. Т.е не смотря на то, что эти значения определяются субъектами
(адекватным выбором масштаба, уровнем развития технологии и т.п.), объективность
самих таких понятий обусловлена независимостью их от каких-либо возможностей
субъектов в том смысле, что изменением масштабов, развитием технологий и т.п.
нельзя исключить эти понятия – обходиться без них. Расстояние между объектами,
скорость относительного движения которых имеет глобальный экстремум, будем
называть бесконечным расстоянием. В
зависимости от того, является ли этот экстремум максимумом или минимумом,
расстояния будем называть соответственно бесконечно большим или бесконечно
малым. Объекты, удаленные друг от друга на бесконечно большие расстояния,
называются изолированными друг от
друга, а объекты, расстояние между которыми конечно называются взаимодействующими. Система объектов,
удаленных друг от друга на бесконечно малые расстояния, называется составным объектом.
Таким
образом, изолированные друг от друга объекты и части составного объекта, не
обязательно взаимно неподвижны, но обязательно имеют неизмеримые/бесконечные относительные
ускорения, в отличие от взаимодействующих объектов, имеющих измеримые/конечные
ускорения. Заметим, что если значение величины нельзя измерить, то фактически
это означает, что такие значения
отсутствуют, т.е. равны нулю. Исходя из этого, в традиционной физике считают,
что изолированные друг от друга объекты не имеют относительного ускорения – оно
рано нулю а, следовательно, относительные скорости удаленности их сохраняют
свои постоянные значения. Соответственно сохраняются значения характеристик
изолированных объектов – нельзя зафиксировать изменения характеристик таких
объектов. Принципиальным здесь является то, что относительные движения никоим
образом не связаны ни с какими-либо искусственно введенными в традиционную
физику непосредственными действиями объектов друг на друга. Не связаны относительные
движения и со свойством инерции масс, и ни с каким-либо понятием метрического пространства,
в котором они расположены, и уж тем более, ни с одним из свойств его (например,
кривизной). Другими словами, можно обойтись без использования этих понятий,
которые в силу того, что они являются интуитивными, существенным образом
ограничивают область применения получаемых выводов.
Процесс,
при котором два объекта, удаленные друг от друга на конечное расстояние,
стремятся к бесконечно малому расстоянию, называется поглощением этих объектов друг другом. В конце концов, объекты
становятся одним составным объектом, т.е. пропадает возможность установить
предшествование одного другому, что эквивалентно упоминавшемуся выше понятию
смерть одного из объектов. Процесс, при котором два объекта, удаленные друг от
друга на бесконечно малое расстояние, стремятся к конечному расстоянию между
ними, называется излучением
составного объекта своей части. В результате возникает возможность установить
предшествование этих объектов, что эквивалентно упоминавшемуся ранее понятию
рождение нового объекта. Понятно, что при излучении и поглощении объектов характеристики
их должны меняться на конечные значения, ни меньшие чем кванты. Это
подтверждается экспериментально законами Планка, которые дают количественную
оценку таким дискретным изменениям. Не следует считать, что при поглощении
объекта – его смерти – общее количество всех существующих в природе объектов
уменьшается. Такое допущение противоречит тому, что физические объекты могут
существовать (в соответствии с принятым выше определением их) только в
количестве не менее трех. Действительно, в случае рассмотрения трех объектов
при взаимном поглощении двух из них, общее количество должно было бы стать
меньше трех. Следует считать, что как смерть, так и рождение объектов означает
изменение возможности субъектов идентифицировать их, т.е. изменение возможности
наблюдать только эти конкретные объекты относительно каких-то ранее наблюдаемых
объектов. И при этом не пропадает возможность идентифицировать те же самые объекты
относительно и с помощью других всегда существующих в количестве не менее трех наблюдаемых
физических объектов. Такое изменение возможности наблюдений может быть
различным для разных субъектов и объектов, в частности, при использовании ими
различных приборов. Формально можно считать, что смерть одного объекта сопровождается
рождением другого объекта с другими характеристиками, как минимум, с другой
материальной характеристикой. Это согласуется с указанной ранее особенностью
природы и, в частности, с законом «сохранения возможности движения», согласно
которому для любого объекта всегда существует другой объект, относительно
которого может иметь место его движение. Поскольку процедуры рождения и смерти
являются необходимыми для возможности наблюдения (существования) объектов, то
можно сказать, что сами эти процедуры и их чередование и есть суть жизни, как ее
обычно понимают как для субъектов, так и для объектов.
Во
взаимодействиях между объектами участвуют все составные части их. Если считать,
что каждая часть одного объекта одинаково удалена от других объектов – от любой
их части, т.е. если не учитывать удаленности частей внутри каждого объекта, то
количественное различие взаимодействий двух пар объектов при одинаковых
пространственной и временной удаленности их, может быть вызвано только разным
числом составляющих объекты частей. Поэтому, как самим объектам, так и любым
частям их вплоть до квантов, можно сопоставлять параметр, определяющий только различие
числа составляющих их частей при прочих равных условиях. Повторим, что введение
такого параметра оправдано в случае, если удаленности частей внутри каждого
объекта малы по сравнению с удаленностью между самими этими объектами, т.е.
если каждый такой составной объект допустимо рассматривать как единый объект.
Поскольку пространственная и временная удаленности в рассматриваемых случаях сохраняют
свои значения, то упомянутый параметр, определяющий возможное различие
взаимодействий, т.е. различие изменений объектов друг относительно друга, должен
быть связан (должен объясняться или определяться) только с различием материальной
удаленности объектов. Этот параметр, обозначаемый ниже той же буквой что и
объект, называется массой. Подчеркнем, что введенное понятие массы характеризует
только степень того, насколько объект является составным, и определяется лишь
числом частей (в конечном счете - числом квантов материи), из которых состоит
объект. Т.е. физический смысл этого понятия совпадает со смыслом, который
вкладывается в понятие количество материи (вещества, субстанции и т.п.), но не
в понятие качество ее и, следовательно, никаких других свойств типа: создавать
гравитационные поля, обладать инерцией и т.п. массе приписывать нет
необходимости.
В
случае если два наблюдаемых объекта ![]() и
и ![]() изолированы от других
объектов, то, в соответствии с выше указанной особенностью изолированных
объектов сохранять свои свойства, масса такого составного объекта равная
изолированы от других
объектов, то, в соответствии с выше указанной особенностью изолированных
объектов сохранять свои свойства, масса такого составного объекта равная ![]() остается постоянной, и
может измениться только при изменении состояния изолированности его.
Пространственная удаленность этих двух объектов друг от друга, и дифференциалы
всех порядков такой удаленности, могут меняться за элементарные временные
интервалы
остается постоянной, и
может измениться только при изменении состояния изолированности его.
Пространственная удаленность этих двух объектов друг от друга, и дифференциалы
всех порядков такой удаленности, могут меняться за элементарные временные
интервалы ![]() только на одну и ту же
элементарную величину
только на одну и ту же
элементарную величину ![]() . В этом случае,
коэффициент
. В этом случае,
коэффициент ![]() в (8) должен быть тоже
постоянным и пропорциональным сумме масс взаимодействующих объектов, т.е. массе
составного объекта:
в (8) должен быть тоже
постоянным и пропорциональным сумме масс взаимодействующих объектов, т.е. массе
составного объекта:
![]() .
.
Здесь
![]() - коэффициент, который
может быть назван коэффициентом автономного взаимодействия двух объектов
суммарной единичной массы, т.е. такого взаимодействия их, при котором оно не
зависит от взаимодействий каждого из этих
объектов с любыми другими объектами и даже от существования таких других
объектов. Кинематические параметры относительного движения двух объектов в
рассматриваемом случае можно записать в виде суммы двух слагаемых
- коэффициент, который
может быть назван коэффициентом автономного взаимодействия двух объектов
суммарной единичной массы, т.е. такого взаимодействия их, при котором оно не
зависит от взаимодействий каждого из этих
объектов с любыми другими объектами и даже от существования таких других
объектов. Кинематические параметры относительного движения двух объектов в
рассматриваемом случае можно записать в виде суммы двух слагаемых ![]() и
и ![]() , соответствующих автономным движениям (действиям) первого
объекта относительно второго и второго относительно первого:
, соответствующих автономным движениям (действиям) первого
объекта относительно второго и второго относительно первого:
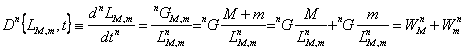 (9)
(9)
Такая
интерпретация не просто соответствует принятому традиционной физикой положению
о сохранении пространственного направления и величины скорости автономных
движений изолированных материальных объектов относительно инерциальной системы
отсчета, что является первым законом Ньютона, но и обобщает это положение на
кинематические параметры любого порядка. Как видно из (9) ![]() , что эквивалентно третьему закону Ньютона о равенстве
действий и противодействий. Не трудно проследить и то, что для приближения
Галилея, т.е. случая
, что эквивалентно третьему закону Ньютона о равенстве
действий и противодействий. Не трудно проследить и то, что для приближения
Галилея, т.е. случая ![]() , выражение (9) соответствует закону всемирного тяготения
традиционной физики. Таким образом, все три закона Ньютона и его закон
всемирного тяготения можно не постулировать, исходя из конечного числа
наблюдаемых опытных результатов, как это принято традиционной физикой, а
получать как следствия принятых исходных положений.
, выражение (9) соответствует закону всемирного тяготения
традиционной физики. Таким образом, все три закона Ньютона и его закон
всемирного тяготения можно не постулировать, исходя из конечного числа
наблюдаемых опытных результатов, как это принято традиционной физикой, а
получать как следствия принятых исходных положений.
Необходимо иметь в виду, что согласно (6), квант
временной удаленности ![]() двух объектов связан с
пространственной удаленностью их -
двух объектов связан с
пространственной удаленностью их -![]() . Поэтому в случае относительного движения объектов этот квант
меняется в процессе движения. Учет этого изменения принципиален лишь в случаях,
когда скорость
. Поэтому в случае относительного движения объектов этот квант
меняется в процессе движения. Учет этого изменения принципиален лишь в случаях,
когда скорость ![]() относительного
движения объектов соизмерима со скоростью сигнала
относительного
движения объектов соизмерима со скоростью сигнала ![]() , и поскольку этот эффект эквивалентен релятивистским
явлениям традиционной физики, то он может быть назван аналогично. Количественно
релятивистский эффект определяется ниже
приведенным выражением (10), в котором удаленности на предыдущем и последующем
этапах наблюдения обозначены соответственно
, и поскольку этот эффект эквивалентен релятивистским
явлениям традиционной физики, то он может быть назван аналогично. Количественно
релятивистский эффект определяется ниже
приведенным выражением (10), в котором удаленности на предыдущем и последующем
этапах наблюдения обозначены соответственно ![]() и
и ![]() . Понятно, что эти удаленности тождественны между собой при
. Понятно, что эти удаленности тождественны между собой при 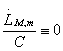 , т.е. при отсутствии движения объектов друг относительно
друга или (что тоже), в случае, если скорость сигнала бесконечно велика по сравнению
с относительной скоростью объектов:
, т.е. при отсутствии движения объектов друг относительно
друга или (что тоже), в случае, если скорость сигнала бесконечно велика по сравнению
с относительной скоростью объектов:
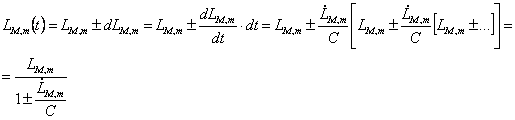 (10) здесь знаки « + » или « - » должны приниматься в
зависимости от того,
(10) здесь знаки « + » или « - » должны приниматься в
зависимости от того,
движется
ли сигнал между двумя объектами в направлении их движения «друг к другу» или
«друг от друга». Понятно, что пространственная взаимная удаленность двух
объектов не должна зависеть от того, на каком из них сигнал рождается, а на
каком он умирает. Для того чтобы исключить такую зависимость можно брать половину
суммы результатов наблюдений этих двух вариантов. К тому же, исходя из возможности
практической реализации процесса
наблюдения, сигнал должен рождаться на одном из наблюдаемых объектов и умирать
на нем же после отражения (процедуры смерть/рождение) от другого объекта, что
как раз и соответствует реализации этих двух вариантов. При этом имеет место
соотношение:
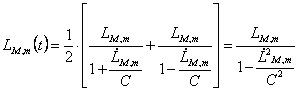 (11)
(11)
Как
видно, формула для релятивистского эффекта в предлагаемом нетрадиционном
подходе похожа на известную из традиционной релятивистской физики зависимость
характеристик объектов от скорости их автономных движений. Принципиальное
отличие этих двух зависимостей состоит в отсутствии в (11) радикала. Заметим, что,
по мнению некоторых ученых такое же отсутствие радикала в формуле для релятивистского
эффекта может быть получено и в рамках классической физики. Например, В. Петров,
см. [22], считает, что исходя из анализа результатов опыта Майкельсона-Морли «Коэффициент сокращения длины должен быть,
принят равным ![]() , а не
, а не ![]() , как это следует из преобразований Лоренца -
Эйнштейна. Таким образом, преобразования Лоренца - Эйнштейна не соответствуют
теории опыта Майкельсона – Морли». Анализ
решения известной проблемы перигелия Меркурия, во многом благодаря которой
теория относительности получила признание научного сообщества, показывает, что применение
формулы (11) в этом случае дает на порядок лучшие приближения к наблюдаемым
результатам, чем это имеет место при использовании упомянутой формулы теории
относительности учитывающей релятивистский эффект.
, как это следует из преобразований Лоренца -
Эйнштейна. Таким образом, преобразования Лоренца - Эйнштейна не соответствуют
теории опыта Майкельсона – Морли». Анализ
решения известной проблемы перигелия Меркурия, во многом благодаря которой
теория относительности получила признание научного сообщества, показывает, что применение
формулы (11) в этом случае дает на порядок лучшие приближения к наблюдаемым
результатам, чем это имеет место при использовании упомянутой формулы теории
относительности учитывающей релятивистский эффект.
12. Энергия –
фундаментальная интегральная характеристика системы объектов
Поскольку
кинематические параметры взаимодействия двух объектов ![]() и
и ![]() зависят от их масс и
расстояния между ними
зависят от их масс и
расстояния между ними ![]() , то для многих целей целесообразно использовать величину,
интегрально характеризующую эту зависимость. В качестве такой величины проще и
удобнее всего взять сумму (интеграл) произведений автономных действий каждой
массы этих объектов на элементарные изменения расстояния между ними во всем
диапазоне изменения состояний. Эта величина имеет вид (для приближения
Галилея):
, то для многих целей целесообразно использовать величину,
интегрально характеризующую эту зависимость. В качестве такой величины проще и
удобнее всего взять сумму (интеграл) произведений автономных действий каждой
массы этих объектов на элементарные изменения расстояния между ними во всем
диапазоне изменения состояний. Эта величина имеет вид (для приближения
Галилея):
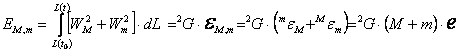 (12)
(12)
где 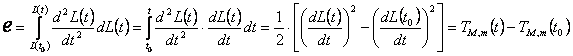
Здесь
![]() и
и ![]() - моменты времени
соответствующие каким-нибудь двум состояниям, из которых одно состояние,
например, с нулевыми индексами предшествует другому, и соответствующие этим
моментам расстояния между объектами
- моменты времени
соответствующие каким-нибудь двум состояниям, из которых одно состояние,
например, с нулевыми индексами предшествует другому, и соответствующие этим
моментам расстояния между объектами ![]() и
и ![]() . Величину
. Величину ![]() называют энергией системы двух объектов
называют энергией системы двух объектов ![]() и
и ![]() , приобретаемой (накапливаемой) в результате взаимодействия
их друг с другом за интервал времени
, приобретаемой (накапливаемой) в результате взаимодействия
их друг с другом за интервал времени ![]() . Величины
. Величины ![]() и
и ![]() могут быть названы
энергиями самих этих объектов, приобретаемыми ими за тот же интервал времени в
результате взаимодействия между собой внутренних объектов составляющих их. Следовательно,
энергия системы вычисляется путем суммирования энергий составляющих частей.
Говорят, что энергия системы сосредоточена в объектах, составляющих систему,
или распределена между ними. Понятно, что поскольку каждая система объектов
может рассматриваться как самостоятельный единый объект, то введенное понятие
энергии является фундаментальной интегральной характеристикой такого объекта
(системы составляющих его объектов), в которой отражены все три фундаментальные
характеристики его. Если объект изолирован от всех других объектов, то согласно
определениям этих понятий значение энергии его не может измениться. Это
положение подтверждается экспериментально и является содержанием «закона сохранения энергии». Тем самым
не нужно приписывать энергии различные формы (гравитационную, тепловую,
электромагнитную, химическую и др.) или считать ее субстанцией (?) и априори
постулировать закон сохранения ее как это делается в традиционной физике. Этот
закон является одним из следствий исходных положений принятых при нетрадиционном
подходе к физике.
могут быть названы
энергиями самих этих объектов, приобретаемыми ими за тот же интервал времени в
результате взаимодействия между собой внутренних объектов составляющих их. Следовательно,
энергия системы вычисляется путем суммирования энергий составляющих частей.
Говорят, что энергия системы сосредоточена в объектах, составляющих систему,
или распределена между ними. Понятно, что поскольку каждая система объектов
может рассматриваться как самостоятельный единый объект, то введенное понятие
энергии является фундаментальной интегральной характеристикой такого объекта
(системы составляющих его объектов), в которой отражены все три фундаментальные
характеристики его. Если объект изолирован от всех других объектов, то согласно
определениям этих понятий значение энергии его не может измениться. Это
положение подтверждается экспериментально и является содержанием «закона сохранения энергии». Тем самым
не нужно приписывать энергии различные формы (гравитационную, тепловую,
электромагнитную, химическую и др.) или считать ее субстанцией (?) и априори
постулировать закон сохранения ее как это делается в традиционной физике. Этот
закон является одним из следствий исходных положений принятых при нетрадиционном
подходе к физике.
По
мере удаления объектов ![]() и
и ![]() друг от друга и от
других объектов
друг от друга и от
других объектов ![]() , т.е. стремления каждого из них к абсолютной изолированности,
будет иметь место согласно (7)
, т.е. стремления каждого из них к абсолютной изолированности,
будет иметь место согласно (7) ![]() и все энергии будут стремиться к
и все энергии будут стремиться к ![]() – неположительным
минимальным значениям. При сближении объектов
– неположительным
минимальным значениям. При сближении объектов ![]() и
и ![]() –
– ![]() вплоть до их
объединения в единый составной объект
вплоть до их
объединения в единый составной объект ![]() , все энергии будут согласно (7), стремиться к неотрицательным
максимальным значениям
, все энергии будут согласно (7), стремиться к неотрицательным
максимальным значениям ![]() ;
; ![]()
![]() . Следовательно, объект не может в результате излучения
приобрести дополнительную энергию, а в результате поглощения объектов потерять
часть своей энергии. Наибольшую энергию система двух объектов приобретает когда
. Следовательно, объект не может в результате излучения
приобрести дополнительную энергию, а в результате поглощения объектов потерять
часть своей энергии. Наибольшую энергию система двух объектов приобретает когда
![]() , т.е. при взаимном поглощении объектов, начинающих
взаимодействовать из состояния абсолютной изолированности –
, т.е. при взаимном поглощении объектов, начинающих
взаимодействовать из состояния абсолютной изолированности – ![]() . Величина такой энергии равна:
. Величина такой энергии равна:
![]() (13)
(13)
Как
указано выше, каждый объект можно рассматривать как состоящий из пар объектов, каждый
из которых первоначально начинается из двух одинаковых квантов, имеющих равные
массы. Поэтому максимальное значение энергии, которое может быть накоплено
составным объектом массой ![]() , определяется согласно (13) следующей формулой, подтверждающей
положения теории относительности:
, определяется согласно (13) следующей формулой, подтверждающей
положения теории относительности:
![]() (14)
(14)
13. Ограниченность
относительной скорости объектов и универсальный сигнал
Отношение
энергии объекта к его массе будем называть плотностью энергии. Максимальные
значения плотности энергии (допустимые природой) и соответствующие им объекты и
состояния будем называть фундаментальными.
Заметим, что формула (14), кроме всего прочего, указывает и то, что относительные
скорости любых частей фундаментального объекта одинаковы и равны ![]() . Поскольку согласно (7) максимальные относительные скорости
объектов достигаются при минимальных относительных расстояниях между ними, то в
фундаментальном объекте все расстояние между составляющими его объектами, и,
следовательно, размеры самого объекта имеют наименьшие конечные значения, по
сравнению с любыми не фундаментальными объектами такой же массы. Примером
фундаментального объекта является нейтронная звезда, плотность материи (отношение
массы к объему), и размеры которой равны
. Поскольку согласно (7) максимальные относительные скорости
объектов достигаются при минимальных относительных расстояниях между ними, то в
фундаментальном объекте все расстояние между составляющими его объектами, и,
следовательно, размеры самого объекта имеют наименьшие конечные значения, по
сравнению с любыми не фундаментальными объектами такой же массы. Примером
фундаментального объекта является нейтронная звезда, плотность материи (отношение
массы к объему), и размеры которой равны ![]() =
= ![]() кг/м3 и
кг/м3 и ![]()
![]() м. Понятно, что фундаментальными могут быть только объекты,
любые составляющие части которых тоже фундаментальны. Все такие объекты имеют
одинаковую плотность энергии равную
м. Понятно, что фундаментальными могут быть только объекты,
любые составляющие части которых тоже фундаментальны. Все такие объекты имеют
одинаковую плотность энергии равную ![]() , а скорость поглощения/излучения фундаментальным объектом
любого другого объекта тоже будет одинакова и равна
, а скорость поглощения/излучения фундаментальным объектом
любого другого объекта тоже будет одинакова и равна ![]() . Для получения численных значений
. Для получения численных значений ![]() , ниже приведены результаты интегрирования дифференциального
уравнения (8) для приближения Галилея, для которого известно значение
коэффициента автономного действия, называемого гравитационной постоянной
, ниже приведены результаты интегрирования дифференциального
уравнения (8) для приближения Галилея, для которого известно значение
коэффициента автономного действия, называемого гравитационной постоянной ![]() м3/(кг×сек2). Без принципиального ограничения
общности, принято, что во всем диапазоне взаимодействия двух объектов, в том числе
и когда
м3/(кг×сек2). Без принципиального ограничения
общности, принято, что во всем диапазоне взаимодействия двух объектов, в том числе
и когда ![]() , оба объекта можно идентифицировать, т.е. отличать друг от
друга. Это будет иметь место в ниже принятом случае, когда один из объектов,
например –
, оба объекта можно идентифицировать, т.е. отличать друг от
друга. Это будет иметь место в ниже принятом случае, когда один из объектов,
например – ![]() , несоизмеримо меньше объекта
, несоизмеримо меньше объекта ![]() , и оба этих объектов являются фундаментальными и,
следовательно, сохраняющие при относительных движениях постоянными свои характеристики.
Чтобы убедиться в том, что полученные результаты не предопределены релятивистскими
эффектами, априори ограничивающими максимальную относительную скорость объектов
величиной
, и оба этих объектов являются фундаментальными и,
следовательно, сохраняющие при относительных движениях постоянными свои характеристики.
Чтобы убедиться в том, что полученные результаты не предопределены релятивистскими
эффектами, априори ограничивающими максимальную относительную скорость объектов
величиной ![]() , ниже приведенные вычисления выполнены без учета этих
эффектов. Кроме того, чтобы оценить влияние формы составного объекта
, ниже приведенные вычисления выполнены без учета этих
эффектов. Кроме того, чтобы оценить влияние формы составного объекта ![]() , с которым взаимодействует
, с которым взаимодействует ![]() , рассмотрены два простейших случая. В одном случае объект
, рассмотрены два простейших случая. В одном случае объект ![]() принят шаром, а в
другом – кубом. Оба они имеют одинаковые объемы -
принят шаром, а в
другом – кубом. Оба они имеют одинаковые объемы - ![]() , равномерно распределенные плотности материи -
, равномерно распределенные плотности материи -![]() и соответственно диаметр и ребро -
и соответственно диаметр и ребро -![]() .
.
Уравнение
(8), в котором в рассматриваемом случае необходимо принять ![]() , имеет следующий первый интеграл:
, имеет следующий первый интеграл:
![]() , (15)
, (15)
где 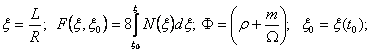
для шара: 
для
куба: ![]() ,
,
где 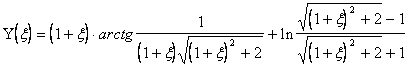
На рис.1 и 2 приведены графики,
иллюстрирующие зависимости соответственно относительного ускорения и скорости -
![]() от взаимной
удаленности двух таких объектов –
от взаимной
удаленности двух таких объектов – ![]() , начавших гравитационное взаимодействие из состояния
абсолютной изолированности их, т.е. при
, начавших гравитационное взаимодействие из состояния
абсолютной изолированности их, т.е. при ![]() . Выражения
. Выражения ![]() получены путем суммирования
взаимодействий объекта
получены путем суммирования
взаимодействий объекта ![]() , удаленного на расстояние
, удаленного на расстояние![]() от центра составного объекта М, с каждой его частью, т.е.
интегрированием по всему объему объекта М (шара или куба). Подставляя в (15)
значение гравитационной постоянной, а также значения размеров и плотности материи
нейтронной звезды (при этом второе слагаемое в величине
от центра составного объекта М, с каждой его частью, т.е.
интегрированием по всему объему объекта М (шара или куба). Подставляя в (15)
значение гравитационной постоянной, а также значения размеров и плотности материи
нейтронной звезды (при этом второе слагаемое в величине ![]() можно не учитывать в
ввиду малости его), получим следующий диапазон значений
можно не учитывать в
ввиду малости его), получим следующий диапазон значений ![]() м/сек для скоростей поглощения объекта
м/сек для скоростей поглощения объекта ![]() фундаментальным шаром
и кубом М . Эти значения с учетом
принятых допущений и точности параметров нейтронной звезды, вполне соответствуют
экспериментально определенной максимальной скорости объектов - скорости света
фундаментальным шаром
и кубом М . Эти значения с учетом
принятых допущений и точности параметров нейтронной звезды, вполне соответствуют
экспериментально определенной максимальной скорости объектов - скорости света ![]() м/сек. Таким образом,
кванты электромагнитного излучения, частным случаем которых являются кванты
света называемые фотоны, могут быть приняты в качестве универсального сигнала,
что практически имеет место не только при научных наблюдениях астрономических
объектов методами радиолокации, но и при любых бытовых визуальных наблюдениях,
о чем говорилось выше. Действительно, чтобы увидеть что-либо свет должен пройти
путь от наблюдаемого объекта до прибора или глаза наблюдателя.
м/сек. Таким образом,
кванты электромагнитного излучения, частным случаем которых являются кванты
света называемые фотоны, могут быть приняты в качестве универсального сигнала,
что практически имеет место не только при научных наблюдениях астрономических
объектов методами радиолокации, но и при любых бытовых визуальных наблюдениях,
о чем говорилось выше. Действительно, чтобы увидеть что-либо свет должен пройти
путь от наблюдаемого объекта до прибора или глаза наблюдателя.
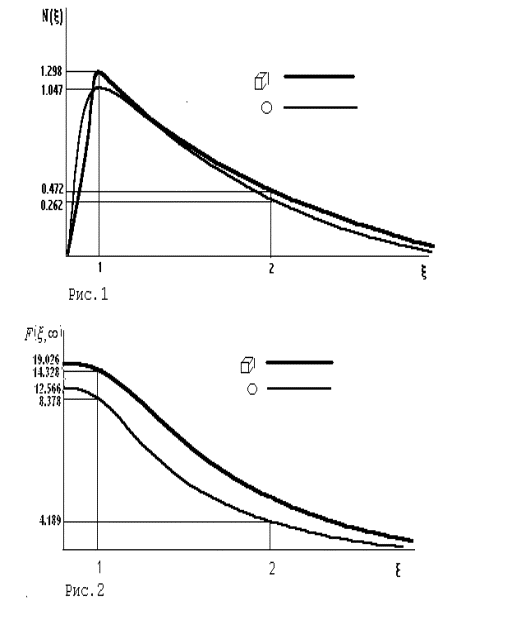
14. Объекты как
колебательные системы
Очевидно,
что поскольку любой физический объект является составным, он может считаться
периодической колебательной системой. Это связано с тем, что составляющие такую
систему объекты могут двигаться друг относительно друга, и в результате этого
характеристики составного объекта будут меняться в диапазоне, определяемом, в
конечном счете, максимальными и минимальными значениями их. Временная и
пространственная характеристики такого объекта могут ассоциироваться соответственно
с периодом и амплитудой (размахом) этих колебаний. Как уже отмечалось практические
возможности субъектов фиксировать характеристики некоторых из таких
колебательных систем, ограничены существованием «горизонта». Такие ограничения
проявляются в случаях, когда удаленности составляющих систему объектов
становятся или бесконечно малыми или бесконечно большими. Отсюда следует, что
по мере приближения к соответствующим экстремумам значения характеристик
объектов становятся экспериментально определяемыми лишь с ограниченными
точностями. Это, а также то, что кинематические параметры определяются
итерационными процессами конечной длительности, и при этом такие процессы
предшествует друг другу, соответствует соотношениям «неопределенности»
Гейзенберга и «дополнительности» Бора, согласно которым параметры не могут быть
экспериментально определены одновременно и с одинаковой точностью.
Наиболее
явно периодичность прослеживается в поведении планет и микро объектов. Относительные
движения таких колебательных систем формально могут рассматриваться как распространения волн,
определяемых своими частотами, скоростью движения и энергией. В частности,
скорость излучения и поглощения квантов материи, обладающих, как и каждый
материальный объект пространственной, временной и материальной
характеристиками, любым другим объектом должна равняться ![]() , поскольку кванты являются фундаментальными объектами. Если
колебания составляющих систему объектов происходят в одной плоскости (это,
например, всегда будет иметь место, если число объектов системы не больше
трех), то они называются поляризованными в этой плоскости. Поскольку согласно
(7) относительные скорости объектов нелинейно зависят от расстояния между ними,
то амплитуда колебаний и энергия системы объектов будут зависеть от частоты
системы -
, поскольку кванты являются фундаментальными объектами. Если
колебания составляющих систему объектов происходят в одной плоскости (это,
например, всегда будет иметь место, если число объектов системы не больше
трех), то они называются поляризованными в этой плоскости. Поскольку согласно
(7) относительные скорости объектов нелинейно зависят от расстояния между ними,
то амплитуда колебаний и энергия системы объектов будут зависеть от частоты
системы - ![]() . В первом приближении можно принимать последнюю зависимость
линейной, как это и имеет место в законе Планка для квантов. При этом получим:
. В первом приближении можно принимать последнюю зависимость
линейной, как это и имеет место в законе Планка для квантов. При этом получим:
![]() , (16)
, (16)
где ![]() кг м2 /с -
постоянная Планка.
кг м2 /с -
постоянная Планка.
Представление
о порядках значений характеристик кванта материи может дать рассмотренная выше
расчетная модель двух объектов М и m, в
которой оба этих объекта нужно рассматривать как кванты. Будем считать, что эти
кванты являются одинаковыми шарами массой ![]() , поглощение которых друг другом происходит с относительной
скоростью
, поглощение которых друг другом происходит с относительной
скоростью ![]() при «касании» квантов,
т.е. при
при «касании» квантов,
т.е. при ![]() . С учетом (14), (15) и (16), в которые надо подставить
. С учетом (14), (15) и (16), в которые надо подставить ![]() , получим следующие два соотношения для характеристик кванта:
, получим следующие два соотношения для характеристик кванта:
![]() м/кг, (17)
м/кг, (17)
![]() кг с
кг с
15. Гравитационное
взаимодействие и два состояния тепловой смерти вселенной
Движение
с ненулевым относительным ускорением двух объектов изолированных от всех других
объектов называют «гравитационным
взаимодействием» этих двух объектов. Существуют два симметричных –
качественно противоположных вида таких движений, отличающихся пространственной направленностью
движения каждого из участвующих в них объектов: «друг к другу» и «друг от
друга», т.е. взаимным сближением и удалением объектов. Оба эти движения
является монотонными, и в силу существования «горизонта», каждое из них
заканчивается тем, что пространственная удаленность между объектами достигает одного
из двух экстремумов – минимума или максимума. При этом расстояние между
объектами становится соответственно бесконечно малым или бесконечно большим.
Монотонность каждого из движений обусловлена невозможностью всех других
объектов, в силу изолированности их, влиять на поведение рассматриваемых двух
объектов. Поскольку при обоих этих экстремумах относительные ускорения двух
рассматриваемых объектов принимают нулевые значения, то объекты после окончания
гравитационного взаимодействия становятся изолированными еще и друг
относительно друга, и тем самым относительно всех существующих объектов –
становятся абсолютно изолированными. Это позволяет говорить, что при
гравитационном взаимодействии объекты стремятся к состоянию абсолютной
изолированности их. Понятно, что после достижения объектами одного из двух
экстремумов гравитационное взаимодействие, если и может возобновиться
(появиться возможность определения относительного ускорения их), то только при
относительном движении, качественно противоположном предыдущему. Т.е. если до
достижения экстремума объекты сближались, то после достижения экстремума
объекты могут лишь удаляться друг от друга, и наоборот. Таким образом, можно
говорить, что гравитационное взаимодействие является проявлением стремления
объектов восстановить абсолютную изолированность их, нарушение которой и является
причиной возникновения гравитационного взаимодействия. Другими словами, два
качественно противоположных вида относительных движения при гравитационном
взаимодействии объектов могут лишь чередоваться и перемежаться состоянием
абсолютной изолированности каждого из объектов, и каждое из этих трех состояний
может считаться причиной или следствием других этих состояний. С учетом того,
что гравитационное взаимодействие двух объектов является процессом, т.е.
протекает с затратой времени, допустимо говорить, что этот качественно
обратимый процесс является периодическим и для него время обратимо. Что
касается количественной обратимости таких процессов, то она имеет место, как
указывалось выше, только в рамках второго приближения – приближения Галилея.
Качественное
изменение гравитационного взаимодействия двух объектов, т.е. переход этих
объектов в обычное взаимодействие может произойти только при уменьшении до
конечной величины расстояния между каким-нибудь третьим объектом и
рассматриваемыми двумя объектами. Это возможно, поскольку другие объекты
(согласно определению, физические объекты существуют в количестве не меньше
трех) тоже могут двигаться друг относительно друга, и могут приблизиться к
рассматриваемым двум объектам на конечные расстояния. Понятно, что при качественном
изменении гравитационного взаимодействия двух объектов (при этом они перестанут
быть изолированными от всех других объектов) изменится аналитический вид
взаимодействия таких объектов до этого определявшийся (9). Такое изменение
взаимодействия объектов должно осуществляться в соответствии с соотношениями
(1), определяющими значения удаленности между тремя не изолированными друг от
друга объектами. В процессе обычного (негравитационного) взаимодействия двух
объектов пространственная удаленность их тоже может иметь экстремумы, но они
будут только локальными. После каждого из таких экстремумов будет
реализовываться одно из двух относительных движений – сближение или удаление этих
двух объектов. При этом не обязательно будет иметь место чередование
относительных движений в качественном отношении, т.е. сближение объектов не
обязательно должно смениться удалением их, и наоборот, как это имеет место при
гравитационном взаимодействии.
Основываясь
на этих рассуждениях можно прийти к выводу, что в случаях любого счетного числа
неизолированных друг от друга объектов возникновение взаимодействия их (каждой
пары объектов) являются тоже следствием нарушения абсолютной изолированности
объектов, а сами процессы относительных движений – это стремление восстановить
ее. Понятно, что наблюдать и осмысливать поведение всех существующих в природе
пар объектов, в таком же объеме как это допустимо для двух объектов,
практически не возможно, и единственный выход – это наблюдать за ансамблями
объектов, используя методы стохастических процессов. Именно этим и занимается получившая
в последнее время развитие так называемая «Теория хаоса», некоторые положения
которой изложены в интересных монографиях ранее упоминавшегося И. Пригожина см.
[16] и [18], внесшего в эту теорию существенный вклад. Согласно этой теории и
для ансамблей может иметь место указанное выше чередование состояний
изолированности и взаимодействия их между собой. Подтверждением этого является
существование так называемых «химических часов», реализуемых, например, в
реакции Белоусова-Жаботинского, в которой наблюдаются периодические сближения и
удаления миллиардов молекул участвующих в этой реакции веществ. Ясно, что по
мере увеличения числа наблюдаемых взаимодействующих объектов, уменьшается
вероятность возникновения состояний их абсолютной изолированности (возможности
фиксирования субъектом таких состояний), сокращается продолжительность
пребывания в таком состоянии и увеличивается длительность процесса взаимодействия.
Исходя
из изложенного, можно с большой степенью уверенности предположить
(экспериментально проверить или опровергнуть это по понятным причинам
невозможно), что поведение системы всех объектов вселенной будет происходить в
качественном отношении в соответствии со сценарием гравитационного взаимодействия
двух объектов. Имеется в виду, что допустимо пребывание всех объектов вселенной
в двух глобальных (фундаментальных) состояниях абсолютной их изолированности,
при которых они расположены наиболее и наименее компактным образом. Т.е. все
объекты удалены друг от друга соответственно на бесконечно малые и бесконечно большие
расстояния. Эти два состояния можно называть состояниями тепловой смерти вселенной, и они должны чередоваться с
промежуточным для них состоянием, при котором объекты взаимно удалены на
конечные расстояния. Это состояние, в котором находится вселенная сейчас, можно
назвать состоянием жизни. До тех
пор, пока не будет установлена причина существования такого чередования, т.е.
пока не будет достоверно установлена возможность существование какого-то
другого «метафизического» состояния, отличающегося от состояний смерти и жизни,
прогнозируемый периодический процесс поведения всех объектов вселенной может
считаться естественным (фундаментальным законом). Учитывая все выше изложенное,
обнаружить третье упомянутое «метафизическое» состояние ни практической, ни
даже теоретической надежды не существует. В настоящее время некоторые
экспериментальные данные космологии позволяют предполагать, что вселенная
находится в таком «состоянии жизни», когда все объекты ее, стремясь достичь абсолютной
изолированности, удаляются друг от друга. Изложенные рассуждения укладываются в
рамки положений, на которых основана теория о, так называемом, Большом Взрыве.
Согласно этой теории современному состоянию вселенной предшествовало состояние,
при котором все физические объекты (вся материя) расположены наиболее компактным
образом - минимально удалены друг от друга. Исходя из этого, характеристики
всей системы объектов можно отсчитывать от эксклюзивного состояния называемого
«начальным». Формально можно считать, что в этом состоянии существовал лишь
единственный материальный объект, из которого в последствии возникли все другие
материальные объекты. Теологи могут пытаться связывать такой единственный
объект с понятием Бог-творец, часть которого имеется в каждом объекте и субъекте.
16. Радиально-тангенциальные
взаимодействия объектов
Взаимодействие
двух объектов М и m, изолированных от всех других объектов, выше названное
гравитационным, является взаимно притягивающим,
т.е. таким, что относительная
скорость их увеличивается по мере их сближения и уменьшается по мере удаления.
Это обусловлено существованием (не равных нулю) квантов пространственной ![]() и временной
и временной ![]() удаленностей, и прямо
пропорциональной зависимостью между ними, имеющей место благодаря понятию
скорости движения сигнала, являющейся максимально допустимой и, следовательно,
постоянной величиной. Кроме того, это обусловлено еще и тем, что в качестве
независимой принята временная характеристика объектов и, следовательно,
знаменатели кинематических параметров, количественно определяющих
взаимодействия, пропорциональны взаимной удаленности объектов в соответствующей
степени, см. (8). Заметим, что существования экспериментально наблюдаемых на
микроуровне дискретных изменений объектов (существования квантов энергии,
массы, длины, времени и др.) лишает возможности какого-либо логического
обоснования, выбора в качестве исходной парадигмы традиционной физики континуальность,
и связанного с этим выбором основополагающего понятия пространственно-временного
континуума. Такой выбор был сделан классической физикой на ранних этапах
развития цивилизации, когда существовавшие технологии не позволяли обнаруживать
дискретный характер всех физических
явлений на фундаментальном уровне. В дальнейшем, когда дискретность явлений
стала достоверно наблюдаемой, традиционная физика, пытаясь сохранить хоть
как-то понятие континуальности, вынуждена постулировать существование двух
можно сказать принципиально различных физик: макро и микро физики, для которых
имеют место следующие диаметрально противоположные закономерности. В макро физике
исходят из существования непрерывных изменений объектов в
пространственно-временном континууме – непрерывных изменений пространственных,
временных и материальных характеристик объектов. Можно сказать, что тем самым постулируется
существование и непрерывность действий объектов друг на друга или
непосредственно с помощью сил, как в механике Ньютона, или посредством искривления
пространства, как в общей теории относительности. Что касается микрофизики, то
в ней тоже сохраняются представления о пространственно-временном континууме и о
взаимодействиях объектов. А для того, чтобы привести в соответствие такие
представления с экспериментально наблюдаемой на микро уровне дискретностью явлений,
предполагают существование каких-то носителей этих взаимодействий, которыми
обмениваются физические объекты. И это, не смотря на то, что такие носители для
наиболее изученного гравитационного взаимодействия, так называемые «гравитоны»,
непосредственно и достоверно обнаружить, не удается. Указанное разбиение на две
физики представляется в свете изложенного искусственным, т.е. обусловленным не объективно
существующим и принципиально неустранимым различием закономерностей у макро и
микро объектов, а лишь неспособностью разработать единый подход к описанию
поведения макро и микрообъектов в рамках принятого как исходное математического
понятия пространственно-временного континуума.
удаленностей, и прямо
пропорциональной зависимостью между ними, имеющей место благодаря понятию
скорости движения сигнала, являющейся максимально допустимой и, следовательно,
постоянной величиной. Кроме того, это обусловлено еще и тем, что в качестве
независимой принята временная характеристика объектов и, следовательно,
знаменатели кинематических параметров, количественно определяющих
взаимодействия, пропорциональны взаимной удаленности объектов в соответствующей
степени, см. (8). Заметим, что существования экспериментально наблюдаемых на
микроуровне дискретных изменений объектов (существования квантов энергии,
массы, длины, времени и др.) лишает возможности какого-либо логического
обоснования, выбора в качестве исходной парадигмы традиционной физики континуальность,
и связанного с этим выбором основополагающего понятия пространственно-временного
континуума. Такой выбор был сделан классической физикой на ранних этапах
развития цивилизации, когда существовавшие технологии не позволяли обнаруживать
дискретный характер всех физических
явлений на фундаментальном уровне. В дальнейшем, когда дискретность явлений
стала достоверно наблюдаемой, традиционная физика, пытаясь сохранить хоть
как-то понятие континуальности, вынуждена постулировать существование двух
можно сказать принципиально различных физик: макро и микро физики, для которых
имеют место следующие диаметрально противоположные закономерности. В макро физике
исходят из существования непрерывных изменений объектов в
пространственно-временном континууме – непрерывных изменений пространственных,
временных и материальных характеристик объектов. Можно сказать, что тем самым постулируется
существование и непрерывность действий объектов друг на друга или
непосредственно с помощью сил, как в механике Ньютона, или посредством искривления
пространства, как в общей теории относительности. Что касается микрофизики, то
в ней тоже сохраняются представления о пространственно-временном континууме и о
взаимодействиях объектов. А для того, чтобы привести в соответствие такие
представления с экспериментально наблюдаемой на микро уровне дискретностью явлений,
предполагают существование каких-то носителей этих взаимодействий, которыми
обмениваются физические объекты. И это, не смотря на то, что такие носители для
наиболее изученного гравитационного взаимодействия, так называемые «гравитоны»,
непосредственно и достоверно обнаружить, не удается. Указанное разбиение на две
физики представляется в свете изложенного искусственным, т.е. обусловленным не объективно
существующим и принципиально неустранимым различием закономерностей у макро и
микро объектов, а лишь неспособностью разработать единый подход к описанию
поведения макро и микрообъектов в рамках принятого как исходное математического
понятия пространственно-временного континуума.
Предлагаемый
нетрадиционный подход к построению физики, в котором не используется это
понятие, делает указанное разбиение физики на две не нужным и тем самым радикально
меняет философию физики и частично всего естествознания. Проявляется это в том,
что поскольку изменения объектов наблюдаются субъектом только друг относительно
друга, и при этом используются только лишь сами объекты, то отпадает
необходимость искусственно вводить в физику представления о силах (взаимодействиях)
или кривизне пространственно-временного континуума, как самостоятельных и объективно
существующих физических понятиях/объектах. С помощью этих понятий в
традиционной физике делаются попытки объяснить механизмы изменений объектов. В
то время как при нетрадиционном подходе вообще отпадает необходимость предполагать
существование каких-либо специальных механизмов изменений объектов, т.к.
достаточно считать, что изменения объектов друг относительно друга являются
естественным состоянием их, которое лишь наблюдается субъектами вышеуказанным
простейшим способом – фиксированием рождения и смерти объектов (изменений их числа
на единицу). Признание того, что изменение объектов является естественным
состоянием их, делает излишним выяснение внешних причин таких изменений. Или,
говоря иначе, если и существуют «причины» изменений объектов, то эти причины
заложены только в самих объектах, а не вне них. В поведении физических объектов
нуждается не то, почему они изменяются, а скорее то, почему в каких-то случаях
они сохраняют свое состояние. Более того, поскольку наблюдения любого объекта
осуществляется субъектом относительно и с помощью других объектов, то уже это не
позволяет достоверно определить, заложена ли «причина» изменений поведения каждого
объекта внутри его самого или в других объектах. Строго говоря, нельзя исключать
даже того, что на изменения объектов в
какой-то степени влияет наблюдаемый субъект – выбор способа наблюдения. По
поводу последнего утверждения ведутся продолжительные дискуссии в квантовой
механике, например, см. [9]. Таким образом, принятый в настоящей работе подход
сближает восприятие и понимание объектов и субъектов, поскольку поведение последних,
в конечном счете, определяется непосредственно лишь внутренними побуждениями,
хотя можно считать, что в некоторых случаях на них оказывают косвенное влияние
другие субъекты и объекты.
Известно,
что в природе существуют не только гравитационные, но и другие взаимодействия
объектов, например, так называемые электростатические (взаимно отталкивающие и
притягивающие взаимодействия), электромагнитные, тепловые, химические и другие
взаимодействия. Отличительной особенностью всех таких взаимодействий является
то, что они проявляются только в случае взаимодействия не менее трех
неизолированных друг от друга объектов, или, точнее говоря, в случае
возможности реализации процедуры наблюдения за тремя и более материальными
объектами. В частности, возникновение ситуации при которой какой-либо третий
объект Q становится неизолированным от двух выше рассматриваемых объектов М и m,
может привести к изменению гравитационного взаимодействия между М и m не только
количественно, но и качественно. Например, в зависимости от изменения расположения
объекта Q относительно М и m, взаимно притягивающее гравитационное взаимодействие
последних объектов может трансформироваться в электростатическое или в электромагнитное
взаимодействие. Для иллюстрации этого, и в первую очередь, для определения понятия последних взаимодействий,
необходимо предварительно уточнить определение тангенциального и радиального
относительных движений объектов.
Для
трех и более объектов (а лишь в таком количестве объекты существуют в природе) относительное
движение двух из них, может иметь место только при относительном движении, как
минимум, еще другой пары объектов, одним из которых должен быть хотя бы один объект
исходной пары. Другими словами, невозможно движение только одной какой-нибудь
пары объектов, без того, чтобы в результате не реализовывалось относительное
движение еще и другой смежной пары объектов, одним из которых был бы
какой-нибудь объект первой пары, или – без того, чтобы не быть результатом
движения другой такой смежной пары. При этом каждое из относительных движений
этих смежных пар имеет место лишь в рамках одной процедуры, а не представляет
собой два различных процесса, предшествующих друг другу. Невозможность относительного
движения только одной пары объектов обусловлена фундаментальными соотношениями
(1) (или сама обуславливает их), связывающих между собой три удаленности между
тремя парами трех не изолированных друг от друга объектов. Таким образом, принятое
традиционной физикой положение о том, что отдельные физические объекты обладают
электростатическими, электромагнитными и даже гравитационными свойствами, т.е.
такие свойства существуют в объектах самостоятельно и вне связи с существованием
как минимум двух других объектов, можно считать не имеющим под собой
экспериментального обоснования. Такие свойства «в чистом виде» зафиксировать принципиально
нельзя – они проявляются только в виде относительных движений как минимум трех
объектов. Похожие взгляды о том, что объекты с такими свойствами сами по себе –
вне наличия других объектов – самостоятельно существовать не могут как
физические объекты, высказывались и ранее, см. [5] стр. 166: «Электроны, электрические и магнитные поля,
эфирные волны – не более чем имена переменных, входящих в формулы; как заметил
по этому поводу Гельмгольц, в теории Максвелла электрический заряд является
лишь носителем символа». Как показывают многочисленные эксперименты, ни
электрические, ни магнитные заряды, ни даже гравитационные массы самостоятельно
(в единственном числе) не существуют как физические объекты. Невозможно
наблюдать ни появление, ни исчезновение, ни наличие только одного из этих объектов
без соответственно появления, исчезновения, наличия другого физического объекта
– не существуют ни электрические, ни магнитные монополи. Последним обстоятельством
объясняется, в частности, то, что при возникновении электростатического или
магнитного заряда одного знака возникает заряд противоположного знака.
Два
объекта могут совершать два качественно отличающихся между собой относительных
движения в зависимости от того, максимально или минимально меняется расстояние
между этими объектами по сравнению с изменениями расстояний каждого из них до
других объектов. Относительное движение объектов m и М будем называть радиальным, если изменение (увеличение
или уменьшение) расстояния между ними максимально по сравнению с изменением
расстояния каждого из этих объектов до любого другого объекта системы, не
лежащего на одной прямой с указанными объектами. Движение объектов q и Q будем называть тангенциальным, если имеет место прямо противоположное предыдущему,
т.е. минимальное изменение расстояния между этими объектами, или, иначе говоря,
если на каждых этапах наблюдения расстояние между q и Q остается постоянным. Траекториями
радиальных и тангенциальных движений являются, соответственно прямые (радиусы),
на которых расположены объекты m и М, и окружности с центрами в Q или в q и радиусом, равным расстоянию между q и Q. Говорят,
что при радиальном относительном движении двух объектов остается постоянным
пространственное направление движение, но максимально меняется взаимная
удаленность их, а при тангенциальном движении - сохраняется взаимная
удаленность их, но максимально меняется пространственная направленность
движения. Если имеет место радиальное или тангенциальное движение объектов М и m, и соответственно тангенциальное или радиальное
движение другой пары объектов M и Q или m и Q одним из которых является объект предыдущей пары,
то говорят, что прямые mM и mQ взаимно
перпендикулярны. Направления
радиального и тангенциального относительного движения разных пар этих трех
объектов взаимно параллельны. А
направления радиального и тангенциального относительных движений каждой пары перпендикулярны
друг другу.
При
этом оба типа последних движений асимметричны друг по отношению к другу. Это
означает, что движение одного типа какой-нибудь из выше указанных пар, например,
М и m является движением другого типа смежной пары объектов
Q и m, и наоборот.
Скорости и другие кинематические параметры радиальных и тангенциальных
относительных движений объектов, будут иметь направления движений соответствующих
пар объектов и количественно определяться производными по времени от расстояний
между этими объектами. Очевидно, что два объекта, изолированные от всех других
объектов, могут совершать относительные движения только с нулевым
тангенциальным ускорением, в силу определения изолированности объектов,
согласно которому такие объекты могут иметь только постоянные радиальные относительные скорости. Для приближения
Галилея это соответствует второму закону Кеплера утверждающему, что в процессе
движения таких объектов не меняется произведение расстояния между ними на
тангенциальную скорость движения одного объекта относительно другого объекта. Заметим,
что это соотношение может быть получено как следствие принятого вначале соотношения (1) между пространственными
удаленностями трех объектов, рассматриваемых как единый объект – треугольник. Радиальное
и тангенциальное движения могут иметь каждое по две взаимно противоположные
направленности, которым можно приписывать знаки «+» и «–» и называть
соответственно «вперед» и «назад» друг к другу и «по часовой стрелке» и «против
часовой стрелки». Радиальное относительное движение каждого из двух объектов
будем называть «вперед» или «назад» друг к другу в зависимости от того,
уменьшаются или увеличиваются расстояния между объектами. Тангенциальное
относительное движение каждого из двух объектов будем называть происходящим «по
часовой стрелке» в зависимости от того, движется ли соответствующий объект этой
пары «назад» или «вперед» к какому-нибудь другому объекту системы,
расположенному соответственно «слева» или «справа» относительно прямой, проходящей
через этот объект и другой объект пары. В противном случае, тангенциальное
движение происходит «против часовой стрелки».
Убедимся,
что описываемое традиционной физикой поведение электрического заряда в
магнитном поле, качественно совпадает с поведением обычного материального объекта
m, движущегося радиально или тангенциально относительно двух других подобных ему
объектов М или Q расположенных на взаимно перпендикулярных прямых mM и mQ. В
соответствии с этим, и по аналогии с традиционным названием – электромагнитное
взаимодействие зарядов назовем указанное поведение объектов m, М, Q радиально-тангенциальным взаимодействием их.
При этом радиальное движение объекта соответствует электрическому
взаимодействию его, а тангенциальное - магнитному. Аналогично указанной выше асимметричности
радиального и тангенциального относительных движений, имеет место и асимметричность
электромагнитных взаимодействий. В физике говорят, что электрическое
взаимодействие вызывает магнитное взаимодействие и наоборот, или иначе – оба
взаимодействия не могут существовать друг без друга. В соответствии с имеющим
место фундаментальным соотношением (1) кинематические параметры радиального и
тангенциального движений связаны между собой. Такая связь легко может быть
установлена путем дифференцирования по времени соотношения, определяемого
теоремой Пифагора, между катетами ![]() и гипотенузой
и гипотенузой ![]() прямоугольного треугольника
прямоугольного треугольника
![]() ,. На основании этого в традиционной физике (в кинематике)
считается, что ускорение радиального движения объекта пропорционально квадрату
тангенциальной скорости его и обратно пропорционально радиусу кривизны
траектории. При изменении направленности тангенциального движения (его
знака) будет меняться направленность
(знак) радиального движения и наоборот. Аналогичная зависимость, как показывают
эксперименты голландского физика Х. К. Эрстеда (1777 – 1830) и американского
физика Г. О. Роуланда (1848 – 1901), имеет место и для заряда, движущегося в магнитном
поле (сила Лоренца), или для двух параллельных проводников с током, создающих
магнитные поля и взаимодействующих друг с другом. Сила, действующая между двумя
параллельными проводниками (относительное ускорение их), прямо пропорциональна
произведению сил токов в проводниках и обратно пропорциональна расстоянию между
ними. Если учесть, что под током понимается движение зарядов, а сила тока пропорциональна
скорости такого движения, то аналитическое описание взаимодействие зарядов
аналогично существующей в кинематике связи радиального ускорения с тангенциальной
скоростью.
,. На основании этого в традиционной физике (в кинематике)
считается, что ускорение радиального движения объекта пропорционально квадрату
тангенциальной скорости его и обратно пропорционально радиусу кривизны
траектории. При изменении направленности тангенциального движения (его
знака) будет меняться направленность
(знак) радиального движения и наоборот. Аналогичная зависимость, как показывают
эксперименты голландского физика Х. К. Эрстеда (1777 – 1830) и американского
физика Г. О. Роуланда (1848 – 1901), имеет место и для заряда, движущегося в магнитном
поле (сила Лоренца), или для двух параллельных проводников с током, создающих
магнитные поля и взаимодействующих друг с другом. Сила, действующая между двумя
параллельными проводниками (относительное ускорение их), прямо пропорциональна
произведению сил токов в проводниках и обратно пропорциональна расстоянию между
ними. Если учесть, что под током понимается движение зарядов, а сила тока пропорциональна
скорости такого движения, то аналитическое описание взаимодействие зарядов
аналогично существующей в кинематике связи радиального ускорения с тангенциальной
скоростью.
Поскольку
автономные движения любого объекта не зависят от существования других объектов
и согласно (9) пропорциональны своей массе, то кинематические характеристики
трех пар объектов M, m, Q и расстояния между ними ![]() связаны между собой
следующими соотношениями. В этих соотношениях учитывается различие
пространственных направлений радиальных относительных движений объектов по
аналогии с тем, как это сделано в соотношениях (1):
связаны между собой
следующими соотношениями. В этих соотношениях учитывается различие
пространственных направлений радиальных относительных движений объектов по
аналогии с тем, как это сделано в соотношениях (1):
 (18)
(18)
С
учетом (1), соотношения (18) представляют собой полную систему трех дифференциальных
уравнений для определения трех неизвестных – расстояний ![]() между каждыми двумя
объектами. Не трудно убедиться, что в случае движения трёх этих объектов вдоль
одной прямой взаимодействие между крайними объектами, например, М и Q будет
взаимно притягивающим (не гравитационным), а взаимодействия между внутренним
объектом m и крайними объектами будут асимметричны друг другу. Т.е. если с одним
из крайних объектов взаимодействие будет взаимно притягивающим, то с другим –
взаимно отталкивающим. Действительно, подставляя в первое соотношение (18) равенства
между каждыми двумя
объектами. Не трудно убедиться, что в случае движения трёх этих объектов вдоль
одной прямой взаимодействие между крайними объектами, например, М и Q будет
взаимно притягивающим (не гравитационным), а взаимодействия между внутренним
объектом m и крайними объектами будут асимметричны друг другу. Т.е. если с одним
из крайних объектов взаимодействие будет взаимно притягивающим, то с другим –
взаимно отталкивающим. Действительно, подставляя в первое соотношение (18) равенства
![]() , получим:
, получим:
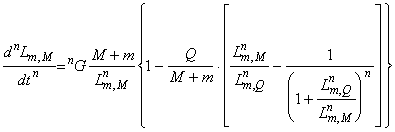 (19)
(19)
Понятно,
что если содержимое фигурных скобок в (19) будет отрицательным, то
взаимодействие М с m будет взаимно отталкивающим. Если еще и ![]() , то это взаимодействие будет электростатическим - обратно
пропорциональным расстоянию между объектами в соответствующей степени n. В зависимости от значений
, то это взаимодействие будет электростатическим - обратно
пропорциональным расстоянию между объектами в соответствующей степени n. В зависимости от значений 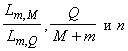 это взаимодействие
может количественно соотноситься с гравитационным взаимодействием, в том числе
и превосходить его даже в рамках второго (галилеевого) приближения, в довольно
широком диапазоне, включая и диапазон 1042, экспериментально
наблюдаемый для элементарного заряда. В соответствии с ранее указанной
аналогией в поведении зарядов в магнитном поле и обычных материальных объектов
M, Q и m, на последние можно смотреть, как на электрические заряды, которые
могут одновременно появится, или исчезнуть (как заряды, но не как физические
объекты), т.е. перераспределиться. Объекты M и Q можно считать зарядами противоположных
знаков, а объект m - зарядом, знак которого совпадает с зарядом М и противоположен
заряду Q или, наоборот, в зависимости от взаиморасположения объектов. Поскольку
относительные скорости объектов не могут превышать скорость универсального
сигнала, то и скорость движения зарядов, т.е. скорость протекания тока тоже не
может превышать скорость такого сигнала. Понятно, что перераспределение зарядов
вызывает перераспределение энергии между объектами, т.е. то, что в традиционной
физике называют переносом её в пространстве. В составном объекте, изолированном
от всех других объектов, сумма зарядов одного знака равна суммарному заряду
противоположного знака – система электрически нейтральна и сохраняет свою энергию.
Изменить энергию или «зарядиться» (имитировать заряд одного знака) система
может лишь при взаимодействии с другими объектами. В результате обязательно
должен возникнуть заряд противоположного знака. В силу того, что характеристики
объектов имеют нижние пределы – кванты значений, то имеет нижний предел и
величина заряда – элементарный заряд.
это взаимодействие
может количественно соотноситься с гравитационным взаимодействием, в том числе
и превосходить его даже в рамках второго (галилеевого) приближения, в довольно
широком диапазоне, включая и диапазон 1042, экспериментально
наблюдаемый для элементарного заряда. В соответствии с ранее указанной
аналогией в поведении зарядов в магнитном поле и обычных материальных объектов
M, Q и m, на последние можно смотреть, как на электрические заряды, которые
могут одновременно появится, или исчезнуть (как заряды, но не как физические
объекты), т.е. перераспределиться. Объекты M и Q можно считать зарядами противоположных
знаков, а объект m - зарядом, знак которого совпадает с зарядом М и противоположен
заряду Q или, наоборот, в зависимости от взаиморасположения объектов. Поскольку
относительные скорости объектов не могут превышать скорость универсального
сигнала, то и скорость движения зарядов, т.е. скорость протекания тока тоже не
может превышать скорость такого сигнала. Понятно, что перераспределение зарядов
вызывает перераспределение энергии между объектами, т.е. то, что в традиционной
физике называют переносом её в пространстве. В составном объекте, изолированном
от всех других объектов, сумма зарядов одного знака равна суммарному заряду
противоположного знака – система электрически нейтральна и сохраняет свою энергию.
Изменить энергию или «зарядиться» (имитировать заряд одного знака) система
может лишь при взаимодействии с другими объектами. В результате обязательно
должен возникнуть заряд противоположного знака. В силу того, что характеристики
объектов имеют нижние пределы – кванты значений, то имеет нижний предел и
величина заряда – элементарный заряд.
Понятно,
что для получения количественного значения элементарного заряда необходимо в
рамках приведенных качественных рассуждений построить соответствующую
экспериментальным данным физическую модель взаимодействий всех не изолированных
друг от друга микро объектов, имеющихся в каждом материальном теле. Хотя
последняя цель и не ставилась в рамках настоящей брошюры, но все же здесь напрашивается
следующее замечание. Как видно из выше приведенного рассмотрения взаимодействия
трех объектов, превышение электростатического взаимодействия над гравитационным
тем больше, чем ближе друг к другу расположены два из них и чем больше суммарная
их масса по сравнению с массой третьего объекта. Таким образом, даже в рамках
простейшей модели из трех объектов возможно качественное представление ядра
атома как скопление двух «массивных» объектов или как один объединенный объект
повышенной массы, а электрон можно представить как менее массивный и удаленный
от ядра объект. Совершенно очевидно, что рассмотрение систем объектов с большим
числом их и с различными расположениями друг относительно друга позволит описать
любые виды взаимодействий объектов, в том числе и так называемые сильные и
слабые взаимодействия. При этом не нужно наделять объекты различными,
качественно отличающимися друг от друга, свойствами. Например, не нужно
считать, что одни объекты могут всегда только притягиваться друг к другу,
т.е. – обладать только гравитационными
свойствами, а другие объекты могут, как отталкиваться, так и притягиваться, с
гораздо большей интенсивностью – обладать электростатическими свойствами или
свойствами так называемых «сильного» и «слабого» взаимодействий. Аналогичная
ситуация имеет место и в отношении электрического тока, протекающего в
проводниках. Имеется в виду, что не обязательно представлять этот процесс как
движение вдоль проводника «свободных электронов» (?), а достаточно,
по-видимому, ассоциировать его с «эффектом домино», в котором роль «падающих»,
правильнее в этом случае говорить – поворачивающихся элементов могут играть нейтральные
материальные объекты, состоящие из трех частей расположенных в вершинах
прямоугольных треугольников. Понятно, что каждый такой элемент имеет
возможность поворачиваться по или против часовой стрелке, чем можно объяснить
возможность протекания тока в проводнике в двух противоположных направлениях и
после каждого «падения/вращения» такой элемент сохраняет возможность осуществлять это неоднократно. Рассмотрение
поведения конкретных систем объектов с количественной точки зрения, способных с
тем или иным приближением описывать различные свойства реальных материальных
объектов на микро уровне, выходит за рамки настоящей работы, и может быть
выполнено усилиями достаточного числа специалистов, разделяющих выше изложенную
парадигму нетрадиционного подхода к физике.
17. Системы отсчета и
нагрузки
Не
трудно убедиться, что поведение системы четырех и большого числа физических объектов
более рационально описывать не набором пространственных удаленностей всех
объектов друг от друга, как это обсуждалось выше, а так называемыми пространственными координатами каждого объекта, с помощью которых можно при
необходимости определять и указанные относительные удаленности. Это связано с
тем, что чем больше число описываемых объектов, тем больше превышение количества удаленностей их друг от друга по
сравнению с числом объектов (координат их) и, следовательно, тем сложнее
описывать поведение системы с использованием лишь взаимных удаленностей ее
объектов. Пространственные координаты объектов должны представлять собой пространственные
удаленности их до какого-нибудь одного физического объекта не входящего в
описываемую систему объектов. Такой объект называют телом отсчета или, учитывая, что любой объект является составным и
его можно представлять как систему других объектов, тело отсчета называют еще и
системой отсчета. Понятно, что желательно,
чтобы эта система не менялась, т.е.
сохраняла свои характеристики, или чтобы изменения этой системы происходили бы
в несравнимо меньшей степени, чем изменения описываемой системы объектов.
Необходимым и достаточным условие этого является постоянство (малая
изменяемость) пространственных удаленностей любых трех ее объектов. С учетом
этого каждый описываемый объект может иметь в этой системе отсчета не более
трех пространственных координат, представляющих пространственные удаленности
его до каждого из трех взаимно неподвижных объектов системы отсчета. В этих случаях
говорят, что такая система отсчета является трехмерной, и это эквивалентно
утверждению о том, что описываемые в ней объекты расположены в трехмерном
пространстве. Если для идентификации каждого описываемого объекта достаточно
лишь двух координат или лишь одной координаты, то такие системы отсчета
называют соответственно двумерной и одномерной. При этом в соответствующих
случаях говорят, что объекты расположены в двух - и в одно мерных пространствах.
В
силу существования ранее определенного понятия «горизонт», для любой описываемой
системы объектов всегда можно с той или иной точностью найти практически неизменяемый
объект (систему трех взаимно неизменяемых объектов), который можно было бы
считать телом отсчета для рассматриваемой системы объектов. Это имеет место,
как для астрономических наблюдений, так и для различных бытовых ситуаций,
например, для так называемых упругих материальных систем (упругих конструкций).
Вначале формализуем само определение
таких конструкций, принципиально не отличающееся от «бытового» представления о
них, и определим физический смысл используемых при этом терминов (в частности
таких как «упругая связь», «собственная форма», «собственная нагрузка» и др.) с
тем, чтобы исключить разночтение в восприятии нижеизложенного. Формализацию
проведем исходя из выше изложенного аксиоматического подхода к построению физики
с тем, чтобы лишний раз
продемонстрировать практическую применимость такого подхода. Под упругой/деформируемой конструкцией
будем понимать такую систему счетного
числа не менее трех материальных объектов, в которой изменение
относительной пространственной удаленности каких-нибудь двух из них приводит к
изменению относительной удаленности любого другого объекта системы относительно
хотя бы одного из этих двух объектов. В соответствии с общепринятой терминологией
теории упругих конструкций говорят, что каждые два таких объекта «связаны друг
с другом упругой связью» или упруго
взаимодействуют друг с другом. Изменение относительной пространственной
удаленности упруго связанных объектов конструкции называют деформированием ее. Как уже говорилось, и как показывают результаты
наблюдений за материальными объектами, которые по определению могут существовать
в количестве не менее трех, изменение относительной пространственной
удаленности двух объектов может быть только следствием изменения пространственной
удаленности хотя бы одного из них относительно третьего объекта. Обратное
положение не всегда имеет место, т.е. изменение относительной удаленности двух
объектов не обязательно приводит к изменению удаленности их относительно
третьего объекта. Примером может служить ситуация, когда два объекта движутся
по окружности, центром которой является третий объект. Не смотря на широкое
применение в теории упругих систем понятия деформирование, довольно часто
предпочитают использовать не язык изменения «удаленностей» объектов друг от
друга, а язык движения каждого из объектов относительно некой «инерциальной системы»
отсчета, как это принято в физике. В
соответствии с такой физической терминологией говорят, что для возможности
каких-либо движений объекта относительно системы отсчета необходимо, чтобы на
него (на каждую его часть, движущуюся вместе с самим объектом как одно целое)
оказывалось какое-либо действие со стороны других объектов. Это действие
называют нагрузкой и говорят, что
необходимым условием деформирования конструкции (изменения относительной
удаленности хотя бы двух объектов ее) является действие на ее разные объекты
разных нагрузок. В частности, надо чтобы
нагрузки действовали не на все объекты конструкции. При этом имеет место прямо
пропорциональная зависимость между величинами нагрузок и степенью
деформирования конструкции. Если деформирование каких-нибудь двух и более
объектов конструкции не представляет интерес, то такие объекты удобнее
рассматривать как единую недеформируемую часть конструкции, т.е. рассматривать
их как один недеформируемый материальный объект конструкции. Каждая недеформируемая
часть должна характеризоваться, помимо своих пространственных координат, еще и
своими размерами – пространственными
удаленностями между объектами, входящими в эту недеформируемую часть. Поэтому
такую часть иногда называют конечным
материальным объектом или
сосредоточенной конечно(раз)мерной массой, в отличие от используемой при
рассмотрении материальных сред так называемой распределенной (континуальной) массы, для идентификации которой не
требуется указания ее размеров. Во многих задачах, в которых участвует
конечномерная масса, для ее идентификации удобнее задавать дополнительно к
пространственным координатам не размеры этой массы, а ее, так называемые угловые координаты, которые могут быть
получены путем арифметических операций с пространственными координатами
объектов составляющих такую массу. Заметим, что угловые координаты используются
для идентификации не только конечномерных, но также и континуальных масс,
размерами которых не задаются. Относительные изменения пространственных и
угловых координат упруго связанных объектов конструкции называются
соответственно нормальными и сдвиговыми
деформациями ее. Принятое
определение упругой конструкции не требуют обязательного рассмотрения «упругих
связей» между ее объектами как конечномерных материальных объектов. Это
положение имеет место не только для континуальной
упругой конструкции, ее еще
называют упругой средой, т.е. такой для которой нет необходимости или
возможности (скорее всего – пока) экспериментально определять значения
относительных удаленностей соседних друг к другу материальных объектов,
называемые в этом случае бесконечно малыми значениями. Это же положение имеет
место и для дискретной системы
материальных объектов, для которой относительные удаленности всех их пар
являются конечными – способными быть определенными непосредственно опытным
путем. Подчеркнем, что выбор континуального или дискретного представления
конкретной упругой конструкции является, в конечном счете, сугубо субъективным
и это необходимо иметь в виду, и относиться скептически к утверждениям о том,
что одно из этих представлений объективно является аппроксимацией (упрощением
или приближением) другого представления. Заметим, что необязательность
рассмотрения «упругих связей» между объектами как конечномерных материальных
объектов может иметь место не только при расчетах упругих конструкций, но и при
рассмотрении других систем объектов, в которых пространственные удаленности
объектов тоже «связаны» друг с другом, например, планет солнечной системы или
других планетарных систем.
Нагрузки,
вызывающие изменения только пространственных координат объектов, называют силами, а нагрузки, вызывающие
изменения только угловых координат объектов, называют моментами. При этом говорят, что силы вызывают поступательные
движения объектов, а моменты – вращательные движения (повороты). На каждый
объект могут действовать независимые друг от друга, как силы, так и моменты. Поскольку,
как уже указывалось, причиной изменения пространственной удаленности друг от
друга двух физических объектов может быть изменения удаленностей от них других
объектов, то относительное деформирования элементов конструкции может быть
вызвано изменением состояния, как внешних объектов, так и внутренних объектов
конструкции. При этом можно говорить, что на участвующие в относительном
деформировании объекты действуют соответственно внешние и внутренние нагрузки. Состояния, которые конструкция
приобретает под действием внешних нагрузок, приложенных к каким либо объектам
ее, иногда называют деформированными (искусственными)
состояниями, а формы деформирования называют вынужденными формами. В случае если конструкция абсолютно изолирована,
т.е. если все объекты конструкции имеет постоянные скорости относительно любых
внешних объектов, то говорят, что внешние нагрузки на конструкцию не действуют
или они отсутствуют. Состояние конструкции в этом случае называют недеформированным (естественным,
тривиальным, исходным и др.) и от этого состояния «отсчитывают» любое другое деформируемое
состояние, которое конструкция приобретает в случае действия на нее внешних
нагрузок, т.е. не изолированности от нее всех внешних объектов. Изолированная
конструкция может приобретать и так
называемые собственные формы деформирования
благодаря существованию внутренних нагрузок. Количество таких форм совпадает с
числом внутренних объектов конструкции. Иногда говорят, что собственные формы
являются вынужденными формами деформирования, приобретаемыми конструкцией
только под действием приложенных к ее объектам внутренних нагрузок. Вынужденные и собственные формы деформирования конструкции могут совпадать друг с другом,
и в этом случае говорят, что эти формы конструкция приобретает под действием собственных нагрузок. Понятно, что
собственные нагрузки должны быть по величине пропорциональны величинам масс объектов,
к которым приложены эти нагрузки и собственным формам конструкции. Это будет
иметь место, например, если тело отсчета совершает так называемые гармонические
колебания относительно конструкции или, что тоже, все объекты конструкции
совершают синхронные колебания относительно тела отсчета. Частоты таких
колебаний называются собственными
частотами, а квадраты их являются коэффициентами пропорциональности между
собственными формами, умноженными на массы, и собственными нагрузками. Иногда
такие собственные нагрузки называют инерционными
нагрузками.
Резюмируя
все вышеизложенное, следует особо подчеркнуть следующие положения.
Нетрадиционный подход к построению физики позволяет, как показано выше,
существенно упростить ее и продвинуться в решении ее основных проблем.
Например, отказаться от представления физики в виде двух наук – макро и
микрофизики, парадигмы которых основаны соответственно на непрерывности и
дискретности фундаментальных физических явлений. Появляется возможность понять,
что собой представляют и почему существуют различные виды взаимодействия
объектов – гравитационные, электростатические, магнитные, сильные, слабые и др.,
а также описывать их с единых позиций. Получают объяснение причина
существования необратимости физических явлений – причина существования «Стрелы
Времени», и другие не вполне ясные при традиционном подходе вопросы. То, что в предлагаемом
подходе к физике различные фундаментальные взаимодействия, получаются как
следствия априори принятых исходных постулатов, а не как экспериментально
установленные факты, приводит к необходимости принципиального пересмотра
взгляда на физику и математику как соответственно чисто эмпирическую и
аксиоматическую науки. Можно даже сказать, что возникает необходимость
пересмотреть взгляд на естествознание как на нечто абсолютно объективное и не
зависящее от человека (субъекта), призванного лишь познавать то, что априори
создано и существует вне связи с ним. Образно говоря, человечество является не
просто читателем книги под названием «Естествознание», но и соавтором такой
книги, будучи неотъемлемой частью природы. Человек является не просто частью
природы, а является такой частью, без которой не возможно и бессмысленно познания
природы. Патетически говоря, создавая природу, Бог пришел к необходимости создания
человека для того, чтобы кто-то мог познать и насладиться его гениальным творением.
И, не создав, в конце концов, человечество,
вряд ли имело смысл, да и возможно было бы заниматься таким творчеством.
Изложенный выше пересмотр взглядов на естествознание имеет не только
философское, но и сугубо практическое значение, которое не может не оказать
существенного влияния на повседневную жизнь.
Как
неоднократно указывалось выше, математика и физика имеют одинаковые как
идеологию построения, основанную на использовании понятия предшествования, так
и конструктивную методологию. Об этом свидетельствует и то, что основное
понятие математики – натуральные числа невозможно осмыслить вне понятия физический
объект, прочем, как и невозможно осмыслить понятия объекты без понятия натуральные
числа. Единство гносеологии математики и физики проявляется также и в том, что
фундаментальные математические константы могут определяться путем проведения
экспериментов с физическими объектами, как это делается в физике при определении
своих констант, например, гравитационной постоянной. В частности,
иррациональное число ![]() можно определять с
помощью известного метода «иглы Бюффона» или, как относительно недавно (в
девяностых годах ХХ века) было показано, с помощью так называемого
«бильярдного» метода. Причем, точность определения этой константы зависит лишь
от числа проводимых опытов. В последнее время все больше становится понятным,
что математические вычисления а, следовательно, и любые логические суждения,
это всегда некий физический процесс на квантовом уровне. На указанное пытался
обратить внимание научного мира еще в 1960 г. американский физик Р. Ландауэр. К
сожалению, в то время среди ученых господствовал взгляд на вычисления как на
некоторую абстрактную логическую процедуру, изучать которую следует математикам,
а не физикам. На эквивалентности математических суждений и физических процессов
основывается идея создания в недалеком будущем, так называемого квантового
компьютера, отличить который от «живого» мозга будет еще труднее (практически
невозможно) чем для современных компьютеров. Имеется в виду, что еще труднее будет
установить такое отличие не при визуальном, а при интерактивном общении
человека с компьютером.
можно определять с
помощью известного метода «иглы Бюффона» или, как относительно недавно (в
девяностых годах ХХ века) было показано, с помощью так называемого
«бильярдного» метода. Причем, точность определения этой константы зависит лишь
от числа проводимых опытов. В последнее время все больше становится понятным,
что математические вычисления а, следовательно, и любые логические суждения,
это всегда некий физический процесс на квантовом уровне. На указанное пытался
обратить внимание научного мира еще в 1960 г. американский физик Р. Ландауэр. К
сожалению, в то время среди ученых господствовал взгляд на вычисления как на
некоторую абстрактную логическую процедуру, изучать которую следует математикам,
а не физикам. На эквивалентности математических суждений и физических процессов
основывается идея создания в недалеком будущем, так называемого квантового
компьютера, отличить который от «живого» мозга будет еще труднее (практически
невозможно) чем для современных компьютеров. Имеется в виду, что еще труднее будет
установить такое отличие не при визуальном, а при интерактивном общении
человека с компьютером.
В
последнее время произошли существенные подвижки во взглядах на естествознание
вообще, и на математику – в частности. Вот мнение современного и
авторитетнейшего математика - россиянина В. И. Арнольда: «Математика является экспериментальной наукой – частью теоретической
физики и членом семейства естественных наук», см. [26]. Математика описывает несоставные
(математические), а физика - составные (физические) объекты. Можно сказать, что
эти объекты отличаются друг от друга соответственно отсутствием и наличием возможностей
наблюдения за изменением количественного состава их, которое приводит к
качественным изменениям объектов. Такие изменения могут происходить только при
рождении или смерти объектов. В свою очередь, различие возможностей таких наблюдений
можно объяснить тем, что для математических объектов эти два события неразличимы
(величина предшествования их бесконечна), а для физических объектов – различимы
(величина предшествования их конечна). Этим объясняется и существование у физических
объектов дополнительных характеристик по
сравнению с математическими объектами. Если использовать физическую
терминологию, то речь идет о том, что
физические объекты имеют массу и могут изменяться во времени в отличие от
математических объектов. При этом совпадение рождения и смерти сигнала в
математике (для математических объектов) эквивалентно тому, что интервал
времени между этими событиями отсутствует, т.е. имеет бесконечные значения, а
для различимых событий в физике интервал конечен. Или можно сказать, что
скорость «движения сигнала в математике» бесконечна, а в физике – конечна.
Таким образом, математика с этой точки зрения может рассматриваться как
предельный случай физики. Более детальное раскрытие единства математики и
физики, учитывая колоссальный объем знаний, накопленных этими древнейшими науками,
едва ли целесообразно в рамках настоящей брошюры.
Известно,
что естествознание развивается двумя, в определенной степени противоположными,
путями. Первый путь – это когда какое-нибудь явление, например, аномальное
поведение перигелия планеты Меркурий (отклонение
от имеющего место для всех других планет) обнаруживается в результате
наблюдений, практически случайно – не в результате целенаправленных
экспериментов по обнаружению именно этого явления. После этого уточняется или
разрабатывается новая теория, объясняющая и количественно описывающая, в том числе
и это явление. Такой путь прошла вся механика Ньютона и почти вся традиционная
физика. Второй путь – это когда явление (например, отклонение света в поле сил
тяжести) фиксируется в результате целенаправленных действий по поиску этого
явления, исходя из уже известной теории, предсказывающей необходимость
существования подобных явлений. Этот второй путь считается более рациональным,
т.к. потенциально он позволяет оптимизировать материальные и временные затраты
и тем самым ведет к скорейшему прогрессу в естествознании. Но этот второй путь
может приводить и к негативным последствиям по сравнению с первым путем, в
случае, если используются неправильные или хотя бы не совсем точные
теоретические посылки. Известно немало случаев, когда были затрачены большие
усилия по поиску явлений, которые, как выяснялось позже, не могут иметь место.
Наиболее известным примером этому является длительная и нерезультативная, с
точки зрения поставленной цели, деятельность в прошлом многочисленных
алхимиков. Современная наука тоже знает немало таких случаев. По-видимому,
наиболее известным из них, является весьма дорогостоящий, и пока безуспешно
продолжающийся (то с большим, то с меньшим усердием), поиск так называемых
«гравитонов». Укажем, что в настоящее время (середина 2006 г.) все еще продолжаются
работы в Старом и Новом свете по реализации двух самых амбициозных и дорогих
таких программ, называемых соответственно GE0600 и L160. И хотя
считается, что отрицательный ответ это тоже результат и в процессе поисков
несуществующего явления могут быть получены новые побочные явления, но все же,
это служит скорее утешением, чем позитивным результатом. Именно поэтому так
важно иметь как можно более корректную теорию физических процессов. Наиболее
ясно это понимают физики-теоретики, о чем свидетельствует, например, эпиграф к
данной брошюре. Понятно, что несвязанные друг с другом теории, объясняющие лишь
отдельные явления, не могут быть конкурентно способны с теорией, описывающей
эти явления с единой позиции. Общеизвестно уже со времен Эвклида, что
наибольшие шансы на успех в этом вопросе могут иметь лишь аксиоматически (но не
эмпирически) построенные теории. Т.е.
теории, построенные исходя из небольшого числа самых общих и очевидных положений,
а не теории, основанные только на различных экспериментально наблюдаемых, но часто
не связанных между собой, физических явлениях – эмпириях. Именно аксиоматически
построенные теории являются, по мнению известного специалиста ХХ века в области
философии науки Карла Поппера, хорошими теориями, поскольку они позволяют
делать предсказания, которые в принципе не могут быть экспериментально опровергнуты.
Традиционная физика, построенная эмпирически, такой «хорошей» теорией не является. Вот
мнение по этому поводу авторитетного специалиста физика Стивена Хокинга: «Любая физическая теория носит временный
характер, в том смысле, что является
всего лишь гипотезой, которую нельзя доказать. Сколько бы раз не констатировалось
бы согласие теории с экспериментальными данными, нельзя быть уверенным в том,
что в следующий раз эксперимент не войдет в противоречие с теорией», см.
[25] стр. 24. Выше изложены начала аксиоматического построения «хорошей», по
определению Поппера, физической теории, способной, по мнению автора, стать
теорией, для которой уместна любимая шутка физиков-теоретиков: «что может быть
более практичнее, чем хорошая теория».
1. Г. Вейл. Математическое мышление, «Наука», М., 1989.
2. Вернер Гейзенберг. Физика и философия. Часть и целое.
М. «Наука», 1990
3.
Р. Фейнман, Р.
Лейтон, М. Сэндс. Фейнмановские лекции
по физике, «Мир», М., 1977
4.
Начала Евклида, книги
1-V1, перевод. Д. Д. Мордухай-Болтовского, М.–Л.,
Гостехиздат, 1948.
5.
Г. Биркофф. Математика и психология, «Сов. Радио», М.
1977.
6.
М. Клайн. Математика.
Поиск истины, М., 1988.
7. Математическая энциклопедия, М., 1977.
8.
Э. Борель.
Вероятность и достоверность. М., 1969.
9.
УФН, Т. 170,2000,
171,2001, 175, 2005 http://www.ufn.ru
10.
А. Эйнштейн, Л.
Инфельд. Эволюция физики, М., 1965.
11.
Н. Т. Роузвер. Перигелий Меркурия, от Леверье
до Эйнштейна, «Мир», М. 1985.
12.
А. Пуанкаре. О науке, «Наука», М., 1983.
13.
Г. Кантор. К обоснованию учения о
трансфинитных множествах, «Наука», М., 1985.
14.
А. В. Погорелов. Основания геометрии, «Наука»,
М., 1968.
15.
УФН, Т. 172, № 2, 2002, http://www.ufn.ru
16.
И. Пригожин, И. Стренгенрс. Время, хаос,
квант. К решению парадокса времени, «ЭдиториалУРРС» М., 2001.
17.
И. Ньютон. Математические начала натуральной
философии/Собрание трудов академика
А.Н. Крылова, том VII. Изд-во АН СССР. – М.-Л.; 1936
18.
И. Пригожин, И. Стренгенрс. Порядок из хаоса.
Новый диалог человека с природой,
«ЭдиториалУРРС» М., 2001.
19.
А. Гейтинг. Интуиционизм. Введение, М., 1965.
20.
А.А. Марков. О логике конструктивной
математики. М., 1972.
21.
Переписка Лейбница и Кларка. Пятое письмо
Лейбница, §45.
22.
В. Петров.
Опыт Майкельсона – Морли и гипотеза Френеля. http://n-t.org/tp/iz/omm.pdf
23.
А.Ю. Грязнов. Абсолютное пространство как идея
чистого разума, журнал «Вопросы философии», № 2, 2004 г., с. 127 – 147.
24.
П.Я. Чаадаев, "Статьи и письма", М.,
изд-во "Современник", 1989 г.
25.
С. Хокинг. Краткая история времени от большого
взрыва до черных дыр. Санкт-Петербург, Амфора 2003.
26.
В.И. Арнольд.
Гюйгенс и Барроу, Ньютон и Гук. Москва, «Наука», 1989.
27.
В.И. Арнольд. Математика и математическое
образование в современном мире. http://www.mccme.ru/edu/index.php?ikey=viam-models7
28.
А. Сухотин.
Парадоксы науки, М.: «Молодая гвардия», 1980. Электронная версия, дата
обновления 3 ноября 2001 года. http://n-t.org//ri/sh/pn05.htm
Dr. Borys Rotgauz, Merziger
Str. 23, 40476 Düsseldorf, Deutschland,
tel. 49 211 9348181,
e-mail: brotgauz@mail.ru
Последние редакционные изменения внесены 23.08.2006