Борис Ротгауз

Показано, как физику можно строить аксиоматически, т.е. получать законы фундаментальных взаимодействий не эмпирически – на основании специальных для соответствующих закономерностей результатов экспериментов, как это имеет место сейчас, а как следствия минимального числа самых общих и очевидных исходных положений. При этом восприятие физики существенно упрощается и становится понятным, что различные фундаментальные взаимодействия представляют собой лишь разные проявления одной и той же сущности, и что современная эмпирическая физика является лишь вторым приближением в описании картины мира.

 

Оглавление

1.    Терминология аксиоматической физики.

2.    Предшествование физических объектов, процессов и состояний.

3.    Причинно-следственные отношения.

4.    Элементарные изменения физического объекта.

5.    Непрерывные наблюдения и изменения величин.

6.    Субъективность понятий «прошлое, настоящее и будущее».

7.    Аксиоматическое построение физики.

8.    Относительные движения объектов.

9.    Взаимодействие объектов и их масса.

10.Гравитационное взаимодействие и два состояния тепловой смерти вселенной.

11.Радиально-тангенциальные взаимодействия объектов.

12.Энергия системы объектов.

13.Релятивистский эффект.

14.Электрические заряды и их взаимодействия.

15.Ограниченность относительной скорости объектов и универсальный сигнал.

16.Объекты как колебательные системы.

17.Проблема необратимости.

18.Ненужность понятия пространственно-временной континуум.

19.Упругие структуры и системы отсчета.

20.Единство математики и физики.

21.Заключение.

22.Литература.

Ниже приведено доказательство того, что физику можно построить аксиоматически по аналогии с тем как это сделал гениальный Эвклид по отношению к геометрии см. [2], начинавшейся подобно физике как наука о наблюдениях. Начнем с дефиниций терминов, используемых ниже в аксиоматической физике, определение которых частично отличается от традиционных понятий эмпирической физики. Предварительно заметим, что под доказательством ниже понимаются рассуждения, которые убеждают. Здесь необходимо согласиться с педантичными читателями в том, что то, что убеждает одних из них не обязательно убеждает  других. Представляется, что проблема доказательства является чисто философской, получить представление, о которой можно, например, в интересной  работе Дэвиса Браиана «Куда движется математика?» см. [16]. В прагматическом плане эта проблема и другие подобные ей (например, что такое истина, что считать красивым, какой ученый, политик, писатель актер и т.д. лучше) решается научным сообществом и обществом в целом на каждом этапе своего развития так называемым демократическим путем – принятием мнения подавляющего большинства индивидуумов. Несогласие отдельных личностей до поры до времени большинством игнорируется, хотя именно такие личности могут являться двигателями прогресса, если им удается убедить такое большинство (иногда и после своей смерти как, например, в случае с Джордано Бруно) в своей правоте. Понятно, что при демократическом выборе крайне желательно учитывать как можно большее число мнений, для чего наука (также как и искусство, политика и т.п.) не должна быть элитарной – доступной пониманию узкой группы специалистов иначе это чревато негативными последствиями, что неоднократно подтверждено всей историей развития человечества. В свете сказанного, одна из целей аксиоматического построения физики это упростить ее.

 Под физикой будем понимать науку, изучающую физические объекты, их называют еще материальные объекты или материальные тела, в отличие от других наук, например, математики, химии, биологии, социологии и др., изучающих свои соответствующие объекты. Будем исходить из того, что понятие физический объект является простейшим и исходным, т.е. таким, которое не может быть определено исходя из более простых понятий в виду отсутствия таковых по определению. Можно считать, что это положение ниже принято в качестве первого постулата аксиоматической физики. Как еще указывал Аристотель, простейшие понятия (неопределяемые более простыми понятиями) должны иметь место, т.к. в противном случае определение любых других понятий было бы бесконечным занятием и, следовательно, оно не имело бы смысла. Это положение справедливо и для всех других априори принятых аксиом – простейших и очевидных утверждений, истинность которых тоже не нужно/нельзя доказывать, т.к. иначе все доказательства были бы тоже бесконечными и лишенными смысла.  С учетом выше принятого первого постулата, нет другой возможности определять физические объекты кроме как с помощью их самих. Исходя из этого, определим физические объекты как то, за изменениями чего субъекты могут наблюдать только относительно и с использованием других физических объектов. Сразу же отметим, что не будь изменений, не только нельзя было бы наблюдать за объектами – отождествлять или отличать их один от другого, что эквивалентно возможности измерять объекты,  но в этом и не было бы необходимости. Как не было бы необходимости наблюдать, например, за своим счетом в банке, уровнем бензина в баке автомобиля и т.п., если бы они не могли меняться. Ниже речь будет идти только о физических объектах, и поэтому такое прилагательное перед словом  объект часто будет опускаться. Физики предпочитают использовать, вместо термина наблюдать, термин идентифицировать – качественно и количественно определять характеристики наблюдаемого. Приведенное определение физических объектов является явным или неявным образом общепризнанным, поскольку именно так реализуются любые наблюдения за этими объектами не только в науке, но и в быту – в повсеместной жизни, и не только при визуальных, но и при любых других наблюдениях. Укажем также, что однозначно измерять и сравнивать между собой можно только такие объекты (их характеристики), которые допустимо осмысливать как ограниченные целые (имеющие свои границы), или как ограниченный набор таких целых. Таким образом, все физические объекты являются ограниченными – имеющими границу, что можно приять в качестве второго постулата.

Сказанное относится и к другим физическим понятиям, и можно даже говорить, что все однозначно осмысливаемые физические объекты и понятия являются ограниченными. Принятое выше определение физики и ее объектов принципиально отличается от традиционного определения эмпирической физики как науки изучающей материю (?), существование и любые изменения которой возможны только в не имею­щем ни внешних, ни внутренних границ пространстве и непрерывном времени – в так называемом «пространственно-времен­ном континууме». Последнее понятие является виртуальным и сугубо математическим (заимствованным из математики), а не физическим понятием. Фактически оно остается таким, даже не смотря на принятое в теории относительности представление о взаимном «влиянии» объектов и этого континуума. Использование виртуального математического понятия «пространственно-времен­ной континуум» в эмпирической физике в качестве исходного понятия приводит к существованию в ней ряда принципиально не решаемых проблем, которые отсутствуют в излагаемой здесь с использованием только физических понятий аксиоматической физике. На это более детально будет указано ниже. Принятое определение физических объектов неявным образом предполагает существование и тех, кто может объекты идентифицировать – существование субъектов. Это лежит в русле так называемого антропологического принципа, существование которого признавали, например такие авторитетные ученые как А.Эддингтон, П. Дирак, Дж. Барроу, Р. Дикке, Б. Картер и др. В формулировке Б. Картера сильный антропологический принцип выглядит так: «Вселенная (и, следовательно, фундаментальные параметры, от которых она зависит) должна быть таковой, чтобы в ней на некотором этапе эволюции допускалось существование наблюдателя», см. [1]. В соответствии с этим принципом, понятие объект и субъект (наблюдатель)  далее рассматриваются как единая дуалистическая пара двух различных понятий, используемых при формулировке термина «наблюдение», и эти понятия не являются независимыми друг от друга. Т.е. предполагается, что субъект и объект – Человек и Природа два связанные между собой понятия, т.к. первое из них мыслится лишь как часть второго, а часть не может осмысливаться без целого, как и целое немыслимо в полном объеме без всех своих частей. Тот факт, что различные субъекты способны воспринимать качественно и количественно характеристики одного и того же объекта одинаковыми свидетельствует не столько о том, что эти характеристики полностью объективны – не зависят от субъектов, а сколько еще и о том, все субъекты обладают одинаковыми возможностями для такого восприятия. Другими словами, на фундаментальном уровне все субъекты имеют и используют одинаковые «механизмы» для восприятия любых физических объектов, т.е. формально можно сказать используют единую «систему отсчета», в каком-то смысле эквивалентную «абсолютной системе» эмпирической физики. В этом и проявляются единство объектов и субъектов и возможность познания их – единство естествознания. Попутно заметим, что с учетом этого, дискутируемый иногда в философии вопрос о том, допустимо ли признавать существования чего-то независимо от возможности наблюдения его, является в практическом плане (в рамках физики) схоластическим – бесплодным и лишенным смысла. Любой ответ на этот вопрос положительный или отрицательный нельзя экспериментально ни подтвердить, ни опровергнуть. Разумнее всего считать, что поскольку человек это и есть природа (ее часть), то и его возможности, в частности возможность, наблюдать саму природу, бессмысленно отделять от нее и формулировать такие вопросы

Аксиоматическую физику определим как науку, исходными положениями которой являются постулаты и аксиомы, а не законы так называемых фундаментальных взаимодействий, устанавливаемые исходя из результатов специальных и часто довольно сложных экспериментов. Под эмпирической физикой будем понимать традиционную физику, в которой исходными положениями как раз и являются полученные эмпирическим путем законы фундаментальных взаимодействий. Специальные эксперименты в аксиоматической физике нужны только для проверки правильности, как исходных постулатов, так и рассуждений, результатами которых являются законы выше упомянутых фундаментальных взаимодействий. Следует отметить, что всякое определение фактически содержит в себе и аксиому, так как, определяя, скрыто утверждают существование того, что определяют, а также и наличие у него соответствующих свойств. По авторитетному мнению А. Пуанкаре, которое он сформулировал по отношению к геометрии, имеет место и обратное положение - «…аксиомы геометрии (я не говорю об аксиомах арифметики) суть не более чем замаскированные определения» (выделение автора цитаты), см. [3], стр.41. Таким образом, можно сказать, что из принятого определения аксиоматической физики и ее объектов вытекают следующие аксиомы. Во-первых, такие объекты являются счетными, т.е.  допускающими сопоставлять каждому объекту одно из натуральных чисел, и при этом для разных объектов эти числа разные. Здесь следует сказать, что само понятие натуральных чисел, являющееся фундаментальным понятием математики и общего естествознания, возникло и осмысливается как раз исходя из процедур  определения физических объектов, каждый из которых воспринимается как нечто единое и неделимое целое, отличающееся от другого неделимого целого. Во-вторых, такие объекты могут осмысливаться и существовать только в количестве не менее трех: два объекта являются идентифицируемыми друг относительно друга, а остальные – это объекты, при использовании которых идентифицируются оба первых объекта. При этом каждый физический объект имеет свои характеристики, позволяющие субъектам различать или отождествлять объекты друг с другом. Сформулированные аксиомы распространяется не только во «вне», но и во «внутрь», т.е. каждый из физических объектов тоже может считаться составным – состоящим из своих не менее трех физических объектов. Это положение можно считать третьим постулатом аксиоматической физики.

Отсюда следует, что каждый физический объект, в силу того, что он составной, имеет более чем одну характеристику. Как минимум, такой объект имеет кроме качества еще и количество соответствующего качества. Для определения всех характеристик физического объекта необходимо наблюдать такую си­стему составляющих его частей или систему объектов, одним из которых является он сам, кото­рая позволяет выявлять свой­­ства этого объекта. В этой системе число  различ­ных пар объектов долж­но сов­па­дать с числом самих этих объектов. При этом соответствующие характеристики состояний всех пар этих объектов однозначно определят искомые характеристики каждого такого объекта ее и тем самым всего физического объекта, который эти пары составляют. Не трудно убедиться, что такой особен­но­стью обла­дает лишь система трех объектов, характе­ризующаяся тремя состо­яниями пар их. Действительно – система двух объектов имеют одну пару, система четырех объектов – 6 пар, система пяти объектов – 10 пар и т.д. Учитывая, что любую систему объектов можно рассматривать как единый физический объект, то минимальное чис­ло однозначно иденти­фици­ру­ю­щих такой объект харак­те­ристик дол­жно сов­­­па­дать с соответствующим чис­лом пар объектов составляющих его, т.е. до­л­­жно ра­в­няться трем. Такие три характеристики связаны друг с другом, т.к. опре­деляются в результате рассмо­трения общей системы таких частей. Эти характеристики не могут отличаться друг от друга количественно, т.к. ха­рактери­зуют один и тот же составной объ­ект. Они отличаются качественно, хотя и должны оп­ре­деля­ться одним и тем же нижеуказанным способом  наблюдения за тремя парами объектов.

Субъекты  могут идентифицировать объекты благодаря тому, что имеют место (будем постулировать это) следующие аксиомы, аналогичные принятым в геометрии аксиомам порядка для точек, например, см. [4] стр. 24-25. Эти аксиомы, которые ниже будем называть тоже аксиомы порядка,  заключаются в том, что для каждых двух и более объектов – двух и более значений любых качественно одинаковых характеристик их, можно установить два противоположных «направления» условно называемые «положительное» и «отрицательное». И по отношению к каждому из направлений любые два объекта (два значения любой качественно одинаковой характеристики их), можно упорядочить друг относительно друга в соответствии с общепринятым представлением о понятии предшествование по прин­­ципу «больше»/«меньше», которое иногда обозначают знаками «>»/«<». Заметим, что понятие предшествование может быть осмысленно только в соответствии с понятием изменение. Объекты и значения их характеристик, для которых можно установить такое предшествование, называют конечными или измеримыми друг относительно друга. Все другие объекты и характеристики, т.е. такие для которых предшествование установить нельзя, называют бесконечными или неизмеримыми друг относительно друга. Имеет место, следующее правило упорядочения: предшествование тому, что в свою очередь предшествует в том же направлении чему-либо третьему, является предшествованием к каждому из них. При таком упорядочении будем гово­рить о направленно ориентированном относительном состоянии объектов наблюдаемой системы их в отношении каждого из качественно одинаковых свойств, или о соответствующей степени удаленности этих объектов друг от друга. Если «направление» меняет­­ся на противоположное, то относительное состояние должно то­же измениться соответственно. Можно говорить, что аксиомы порядка справедливы не только для физических объектов, но также и для любых качественно одинаковых понятий (суждений, восприятий, ощущений и др.). Это связано с тем, что в основе человеческого мышления лежит физический процесс, происходящий на уровне – его иногда называют квантовым, не всегда пока еще в полном объеме доступном для познания, о чем подробнее говориться ниже.

В соответствии с принятым антропологическим принципом, изменения физических объектов должны осмысливаться «наблюдателем» в рамках только трех априори существующих для него восприятий, позволяющих реализовывать наблюдение за объектами и называемых протяженностью, длительностью и материальностью. Последнее восприятие – это возможность определять количество чего-либо, т.е. считать что-либо. С учетом этого, три выше упомянутые характеристики и соответствующие различия каких-нибудь значений их для двух объектов  и , ниже называемые для краткости степени удаленности двух объектов друг от друга, будем называть и обозначать: пространственная - , временная - , и мате­ри­­­аль­ная -  . Нижние индексы у удаленностей указывают на то, что удаленность относится к двум выше указанным объектам, а верхний индекс  определяет степень соответствующей удаленности двух характеристик – указывает глубину, поря­­док, уровень и т.п. соответствующего различия (предшествования) объектов.  Нулевую (самую малую) степень удаленности  называют просто удаленностью, и для нее первую букву  с верхним индексом использовать не будем, т.е. ;  первая степень удаленности соответствует разности значений нулевой удаленности характеристик; вторая степень удаленности соответствует разности значений первой степени удаленности, и т.д. Различные степени удаленности могут быть установлены субъектом в зависимости от необхо­димости и наличия у него практической возмож­но­сти это реализовать, в частности, в зависимости от уровня развития технологий. Говоря другими словами, потенциально субъектом может быть установлена многократная удаленность удаленности каждой из характеристик. Это обуслав­­­ливается тем, насколь­­ко дета­ль­но можно/нужно идентифицировать те или иные объекты и понятия. Ниже будет показано, как это практически осуществляется для физических объектов после определения процедуры наблюдения за изменениями их. Применительно к пространственной характеристике степень удаленности двух объектов связана с порядком кинематических параметров, используемых для описания относительного движения объектов во времени. В частности, нулевая степень удаленности соответствует статическому состоянию объектов, первая степень соответствует быстроте или скорости изменения статического состояния – скорости относительного движения их, вторая степень удаленности соответствует скорости изменения такой скорости и называется  ускорением и т.д.

 Понятно, что изменение пространственной, временной или материальной характеристик одного объекта приведет к изменению удаленностей между ним и другими объектами, имеющими с ним измеримые значения удаленности, чем и определяется связь таких объектов друг с другом. Объекты, имеющие измеримые кинематические параметры второго и более высокого порядка называют взаимодействующими, связанными или неизолированными в пространственном, временном или материальном отношении, а объекты, у которых измеримы кинематические параметры не выше первого порядка, называют невзаимодействующими, несвязанными или изолированными между собой. Объекты, у которых самая малая (нулевая) степень удаленности друг от друга – сама удаленность их – неизмерима, т.е. объекты бесконечно удаленные один от другого, называются взаимно  неподвижными. Таким образом, изолированные объекты могут быть взаимно неподвижными или могут двигаться друг относительно друга, но лишь с постоянной скоростью. Гносеология этих терминов обусловлена объективно существующей для субъектов связью между представлением (ощущением, восприятием и т.п.) о взаимном действии объектов и субъектов друг на друга, как оно понимается субъектами, и возможностью измеримости кинематических параметров различных порядков относительных движений их. В частности, исходят из того, что взаимодействие объектов и субъектов приводит к гораздо более глубоким относительным изменениям их, чем изменения только удаленности их друг от друга, как это кажется на первый взгляд. Ниже принято, что взаимодействие приводит к измеримости кинематических параметров не только второго, но и более высоких порядков. Понятно, что тем самым остается без изменения принятое в эмпирической физике положение о том, что изолированные друг от друга объекты и субъекты не испытывают никакого действия друг на друга и могут сохранять в неизменном виде свое состояние (покоя или движения с постоянной скоростью), называемое состояние инерции.

При монотонных количественных изменениях удаленностей двух конечных или измеримых  друг относительно друга физических объектов в каждом из двух противоположных направлений, т.е. таких изменениях, при которых меняется лишь численные значения характеристик объектов, но не ка­чество и не число их, эти объекты (их характеристики) могут стать бесконечными или неизмеримыми. На определенных этапах таких изменений, которые, как ниже будет показано, всегда происходят дискретно, пропадает практическая воз­мож­ность установить предшествование изменений друг другу – фиксировать степени удаленности значений характеристик (сначала более высокие степени удаленности, а затем и нулевую степень) этих объектов на двух последовательных этапах изменения (наблюдения) за ними. При этом  пропадает возможность установить предшествование хотя бы одного из этих двух объектов любому третьему объекту, всегда существующему в соответствии с принятым выше положением о том, что физические объекты существуют только в количестве не менее трех. Иначе говоря, измеримыми друг относительно друга могут быть только не менее трех физических объектов, одна пара из которых должна служить масштабом для остальных пар объектов наблюдаемой системы. Возможность измеримых физических объектов стать  неизмеримыми друг относительно друга является еще одной фундаментальной особенностью природы. Не следует считать, что при исчезновении возможности уста­­­­­но­­вить ранее существовавшее предшествование (измеримость) объектов общее количество всех существующих в природе объектов уменьшается, т.к. такое допущение противоречит тому, что физические объекты могут существовать (в соответствии с принятым выше определением их) только в количестве не менее трех. Это положение соответствует закону сохранения материи эмпирической физики, в соответствии с которым материя не исчезает и не появляется вновь, а трансформируется. Действительно, в случае рассмотрения трех объектов, если исчезнет возможность установить предшествование двух из них, то общее количество должно было бы при таком допущении стать меньше трех, что не соответствует принятому определению физических объектов. Исчезновение возможности установить предшествование объектов означает лишь изменение возможностей субъекта наблюдать поведение только этих конкретных объектов относительно каких-то ранее наблюдаемых объектов, но при этом не пропадает возможность идентифицировать иные объекты относительно и с помощью других всегда существующих в количестве не менее трех физических объектов. Значение удаленности двух объектов  и М, которому предшествуют все другие значения, будем называть бесконечно большим, а значение, которое само предшествует всем другим значениям – бесконечно малым значением, а оба этих значения будем называть экстремальными значениями. Эти удаленности обозначают соответственно  и . В отличие от измеримых значений удаленности, число которых в общем случае не лимитировано, экстремальных значений для каждой пары объектов всего два. Для разных пар объектов (и даже для одной и той же пары объектов наблюдаемых разными субъектами) экстремальные значения удаленности могут не совпадать друг с другом – могут предшествовать друг другу. Существование экстремальных значений характеристик физических объектов является фундаментальной закономерностью природы. Эта закономерность позволяет выделять из всей совокупности существующих объектов отдельные системы не менее трех объектов пространственно удаленных друг от друга на существенно меньшее расстояние, чем до объектов других систем, и с необходимой для практических нужд точностью считать такие выделенные системы отдельными физическими объектами. Это соответствует выше сказанному о том, что однозначно определять и сравнивать между собой можно только такие понятия (характеристики), которые допустимо осмысливать как нечто целое и ограниченное. Экстремальные значения удаленности могут иметь место при любом (пространственном, временном и материальном) предшествовании физических объектов, и при осмысливании любых физических понятий и суждений, что проявляется в существовании понятия горизонт, ограничивающий наш кругозор в широком смысле слова.

С учетом того, что измеримыми могут быть не менее трех объектов, то и взаимодействовать друг с другом – двигаться относительно друг друга (наблюдать такое движение) могут тоже только не менее трех физических объектов, о чем подробнее будет сказано ниже. Взаимодействие двух объектов называют притягивающим, если кинематические параметры их увеличивается по мере сближения объектов и уменьшаются по мере удаления. Если по мере сближения объектов кинематические параметры уменьшаются, а по мере удаления увеличиваются, то такое взаимодействие называют отталкивающим. Физический смысл трех выше определенных характеристик объектов заключается в том, что они позво­ляют от­ве­чать на сле­дую­щие три вопроса, без кото­рых не воз­мож­­­­­но наблюдение/иден­­­ти­фи­ка­ция материальных объ­­ек­тов друг относительно друга: «как далеко», «как быстро» (или «как часто»), «как много» (или «сколько»). Лю­бые физические объекты и удаленности любых пар их дол­­жны иметь эти три хара­к­те­ри­­сти­ки. Каждая из таких характеристик не может быть осмыслена без  осмысливания двух других, и должна рассматриваться как компонент единой (трехкомпонентной) системы. Можно проследить, что все другие характеристики физических объектов и их систем, например, температура, спин, энергия, энтропия, электрические и магнитные заряды и др., могут быть осмыслены и получены исходя из этих трех характеристик, что позволяет считать их фундаментальными.

Поскольку наблюдать можно совместно не менее трех объектов, то помимо предшество­ва­ния относительных состояний каждой пары их, можно установить еще и предшествование друг другу относительных состояний разных пар объ­­­­ектов, количество которых будет тоже не меньше трех. Понятно, что для каждой пары состояний одного и того же составного объекта или разных объектов тоже могут быть установлены многократные предшествования предшествований состояний друг другу. Тем са­мым не исключается возмож­ность последовательно сравни­вать (упоря­до­чивать) состо­я­ния лю­бого числа физических объ­­ектов и систем их, а также и любые сте­пе­ни отличия их друг от друга. Впрочем, что касается упорядочения любого числа объектов и любой степени предшествований их, то это имеет чисто теоре­­тиче­ское значение, т.к. пра­к­­ти­чески, име­ет смысл говорить только о незна­чительном чис­ле объ­ектов и степеней предшествований, из-за существования вышеуказанного понятия горизонт. Способы фиксирования предшествований связаны с «механизмами памяти», и являются индивидуальными для разных объектов и субъектов. В одних случаях субъекты используют только свою внутреннюю память, а в других случаях  еще и внешнюю память, т.е. дополнительно используют и другие вспомогательные объекты или субъекты. При этом существенную роль играют масштабы – системы объектов (сами объекты) имеющие практически неизменяемые характеристики а, следовательно, и удаленности между собой. В любом случае для фиксирования предшествования, как уже говорилось, необходимо рассмотрение не менее трех объектов или систем их, два из которых должны служить для сравнения с ними любых других пар. В определен­ном смыс­­­ле воз­мож­ность количественно различать значения характеристик объектов, и относительных состояний их эквива­лентна существую­щей в гео­мет­рии возможности использовать понятие «движе­ние», определение которому имеется, например, в [4]  стр.30 позволяющее производить сравнения между со­бой отрезков, углов и других фигур путем наложения их друг на друга. Таким обра­зом, наблюдаемые  физические объек­ты и их пары по­тен­циаль­но могут быть тем или иным образом упорядоче­ны субъектом друг отно­ситель­но друга, по крайней мере, опосредст­во­­ван­но. Измене­ния относительных состояний физических объектов (их систем) назовем физическим про­цессом. Необходимо подчеркнуть следующее принципиальное положение. Понятие предшествования имеет смысл и введено выше только для количественно (но не качественно) отличающихся друг от друга объектов и понятий/суждений, т.е. таких, качественно одинаковые характеристики, которых практически возможно и необходимо различать между собой количественно. Следователь­но, три качественно разные фундаментальные характе­ристики одного и того же физического объекта, которые определены для целостной системы, каковой представляется этот объект, не могут считаться предшествующими друг другу в выше приведенном понимании. Формально можно говорить, что эти характеристики «качественно предшествуют» друг другу – качественно отличаются между собой, но только лишь формально – без какого-нибудь физического смысла. Определение предшествования является так называемой процедурой, и не является физическим процессом, определенным выше как такой, в котором должно иметь место количественное изменение относительных состояний измеримых друг относительно друга физических объектов. Согласно терминологии традиционной физики процедура реализуется вне времени и без изменений в пространстве, в отличие от физического процесса, обязательно осуществляющегося в пространстве и с затратой времени путем использования измеримых друг относительно друга объектов. Иногда, если хотят подчеркнуть, что происходящее не является процессом, и осуществляется без затраты времени и без изменений в пространстве (как это имеет место в процедурах), то это называют событием, явлением или актом. Если определение объектов (их характеристик) или формулировка суждений о них осуществляется в виде процедур, а не физических процессов, т.е. выполняется без использования понятий времени и пространства, то это означает, что применяется математика, а не физика. В соответствии с этим, под элементарными/исходными математическими объектами будем понимать простейшие для осмысливания объекты, восприятие которых осуществляется субъектом автономно – без непосредственного участия чего-либо внешнего относительно себя и объекта. Такие элементарные объекты представляют собой единое и неделимое целое. Согласно этому пространственно-временной континуум, как уже указывалось выше, является одним из элементарных математических объектов. Перефразируя следующее определение, данное Евклидом математической точке: «точкой называется то, что не имеет частей», можно сказать, что элементарный математический объект это то, что не имеет количества, а имеет только качество. Понятие количество применимо лишь к совокупности этих объектов. Математика как раз и занимается изучением в конечном итоге количественных соотношений различных совокупностей таких (лишенных количества) математических объектов, обладающих одним общим для них качеством (свойством). Для подобной совокупности объектов называемых элементами, в математике введен Г. Кантором (1845 - 1918) специальный термин – множество. «Под множеством мы понимаем соединение в единое целое определенных хорошо различимых предметов нашего созерцания или мышления», см. [5]. Как станет ясно из ниже приведенного, математика может рассматриваться как частный (предельный) случай физики, соответствующий бесконечной/неизмеримой относительной скорости изменения объектов. Можно даже говорить, что математика специально разработана субъектами для восприятия естествознания даже в тех случаях, когда отсутствует возможность непосредственного наблюдения за поведением объектов, и этим она существенным образом расширяет возможности познания природы и является неотъемлемой частью естествознания.

 Существование предшествования проявляется в имею­щемся в естествознании понятии причинно-следственная связь. Под причиной понимают такое состояние или процесс, изменение которого предшествует определенному изменению другого состояния или процесса, называемого следствием, и при этом нет необходимости/­воз­мож­но­сти (скорее всего пока) определять иное предшествую­щее этому следствию со­стоя­ние или процесс, изменение которого предшествует такому же изменению следствия. В случае появления у субъекта необ­хо­ди­мо­сти/воз­мо­ж­­но­сти опре­­делить такое состояние или процесс, то последние и бу­дут причиной. По­нят­но, что при из­ме­­­­не­нии «на­прав­ления» предшествования причи­на становиться след­­ствием, а след­ствие причи­ной. Следовательно, между понятиями причина и следствие имеется взаимно однозначное соответствие – одинаковым причинам соответствуют одинаковые следствия и одинаковым следствиям соответствуют одинаковые причины. Процессы и состояния, не имеющие причины, скорее всего из-за того, что отсутствует необходимость или возможность их определять, и, следовательно, не могущие быть измененными, называется соответственно фундаментальными процессами и состояниями природы. Это означает, что фундаментальные состояния и процессы не являются следствиями существования чего-либо другого и не могут быть причинами существования других фундаментальных состояний и процессов. В этом смысле фундаментальные процессы абсолютны и автономны – не зависят ни от кого-либо, ни от чего-либо. Формально допустимо говорить, что фундаментальные физические процессы или состояния являются причинами и следствиями лишь самих себя, т.е. изменения их «предшествуют» лишь изменениям самих себе, и они не зависят от других процессов или состояний. В тоже время, все иные (нефундаментальные) процессы и состояния потенциально могут считаться причинами и/или след­ствиями друг друга. На разных этапах развития цивилизации фундаментальными считались различные процессы и состояния, и не исключено, что и в дальнейшем такие изменения будут иметь место. В математике понятию причинно-следст­вен­­ной связи соответ­ствует понятие функциональной зависимости и при этом причина соответствует аргументу, а следст­вие – функции. Знание и изменение аргумента всегда предшествует знанию и изме­нению функции, и они могут «меняться местами» (по аналогии с причиной и следствием) в зависимости от потребности или удобства анализировать функциональные зависимости. Понятно, что определение функциональных связей это всегда процедура, т.к. осуществляется без привлечения чего-либо внешнего по отношению к аргументу и функции – осуществляется вне времени и без изменений в пространстве. Таким образом, смысл понятия функциональной зависимости в математике однозначно определен существованием причинно-следст­вен­ной связи в физике.

С учетом всего выше изложенного, элементарные изменение любой наблюдаемой системы объектов это следующие два противополож­ных простейших события, при которых про­­исхо­дит увеличение или уменьшение количества наблюдаемых объектов на еди­ницу. В физике эти события называют соответственно излучение и поглощение объекта или возникновение и исчезновение (рождение и смерть) его, и эти события являются доступными для восприятия не только человеку самого малого возраста, но и любому представителю животного мира. В силу того что эти события являются простейшими, однозначно определить механизмы реализации их с использованием более простых событий нельзя, как и нельзя выяснить механизмы предшествования объектов (их характеристик), которое, как указано выше, может быть осмыслено только в соответствии с понятием изменение. Образно говоря, эти механизмы являются интимными или сакральными/таинственными, из чего следует, что возможности наблюдений таких событий могут быть различными для субъектов и объектов, находящихся в различных условиях и, в частности, при использовании ими различных приборов или технологий. С учетом закона сохранения материи формально можно считать, что поглощение одного объекта сопровождается излучением другого объекта с другими характеристиками – как минимум, с другой материальной характеристикой. Поскольку процедуры излучения и поглощения являются необходимыми для возможности наблюдения (существования) объектов, то можно сказать, что сами эти процедуры и их чередование и есть суть жизни/существования физических объектов, как это имеет место и для рождающихся и умирающих субъектов.

Для математических объектов в силу того, что они несоставные не существуют события излучения и поглощения их, и поэтому математические объекты не могут обладать характеристиками физических объектов. Очевидно, что при событиях излучения и поглощения одних объектов другими, пространственные удаленности их друг от друга принимают экстремальные значения. Причем, удаленность между излучившим и излученным им объектом, и удаленность между поглощающим и поглощаемым им объектом  при этих событиях являются бесконечно малой (предшествующей всем другим удаленностям). Такие элементарные события являются не только простейшими и наиболее доступными для восприятия, но и универсальными – лежат в основе любых сколь угодно сложных наблюдений за изменениями физических объектов, которые могут быть зафиксированы субъектом. Иначе говоря, природе достаточен один указанный способ изменения систем физических объектов, чтобы реализовывались любые имеющие место физические явления. Понятно, что при излучении и поглощении объектов характеристики их должны меняться на значения, ни меньшие чем кванты – самые малые измеримые значения удаленности характеристик физических объектов. Это подтверждается экспериментально законом Планка, который дают количественную оценку таким дискретным изменениям. Квантами часто называют и сами эти объекты. То, что согласно опре­делению физических объектов, они мо­гут быть идентифицированы лишь от­но­сительно и с по­мо­щью других объектов, означает, что это возможно в результате наблюдения за поведением ни менее трех объектов ,  и  при двух указанных простейших событиях. В результате таких событий какой-нибудь из этих объектов, например, объект,  ниже назы­ваемый сигна­лом, дол­жен излучаться одним из объектов пары ,   и поглощаться дру­гим объектом этой пары. Естественно, что  излучение и поглощение сигна­ла должны пред­шес­твовать друг другу, в соответ­ствии с приня­тым выше положением о сущест­вовании предшествования любых двух событий и объек­тов (характеристик, со­стояний, явлений и т.п.). Можно даже ска­зать, что существование такого пред­ше­ст­вования эквивалентно самому существова­нию физических объектов (возможности наблюдения за ними) или, говоря иначе – то­му, что характеристики их имеют измеримые или ко­неч­ные значения. Под элементарным этапом наблюдением за физическим объектом будем понимать этап, включающий  эти два элементарных события. Фиксировать эти события субъект может или непосредственно (с помощью своих органов чувств: зрения, слуха, осязания, обоняния и т.п. – некоторые люди утверждают, что они обладают нечувственным восприятием), или опосредствовано – с помощью, например, приборов или других субъектов. При применении любых этих способов результаты неоднократно проводимых наблюдений в одних и тех же условиях, вообще говоря, не должны отличаться  друг от друга, что может служить критерием одинаковости условий наблюдения. Но каждый раз условия абсолютно одинаковыми даже теоретически быть не могут, и не только в силу того, что в результате излучения и поглощения сигнала, уже сами наблюдаемые объекты (их характеристики), строго говоря, изменяются. Но даже если принимать сигнал таковым, чтобы можно было бы игнорировать такие изменения, т.е. предполагать их бесконечно малыми, то все равно нельзя утверждать, что могут быть созданы абсолютно одинаковыми условия наблюдения одного и того же объекта на разных этапах. Это связано с тем, что в соответствии с принятыми выше положениями, сами субъекты и идентифицируемые ими  объекты уже по определению не могут быть полностью определяемыми – детерминированными - из-за того, что идентификация осуществляется субъектами, которые не могут даже сами себя достаточно полно идентифицировать. К субъектам нельзя применять классическую процедуру идентификации – «расчленение» на самостоятельные составные части и последующее «сочленение» их, для более глубокого и детального познания того, что идентифицируется. Субъект (впрочем, как и объект) не может рассматриваться как состоящий из самостоятельных и независящих от друга частей, иначе он перестает быть единым субъектом (объектом). Понятно что, будучи сам недетерминированным, субъект не может в полной мере идентифицировать и физические объекты, хотя степень (глубина) идентификации их может быть в некоторых случаях более высокой, чем для субъектов. Т.е. характеристики объектов могут определяться в каком-то своем диапазоне с гораздо большей степенью достоверности, чем характеристики субъектов, поскольку к физическим объектам применима выше упомянутая процедура «расчленения» и «сочленения» их. Для того чтобы подчеркнуть различие в этом плане между объектами и субъектами, иногда говорят, что объекты принципиально способны познаваться сколь угодно полно, или – потенциально детерминированы, а субъекты – не способны даже в принципе познаваться достаточно полно, или актуально недетерминированы (стохастичны). Степень стохастичности объектов и субъектов связана с тем, насколько близки характеристики их к одному из двух своих экстремальных значений, которые выше определены как такие, за пределами которых вообще невозможно установить предшествование, т.е. определить значения этих характеристик. Вдали от своих экстремальных значений субъекты и объекты могу считаться практически достоверно определяемыми, что находит отражение в том, что в макро физике все законы детерминированы, а в микро физике, изучающей объекты, характеристики  которых близки к бесконечно малым значениям,  законы вероятностные. Последнее не мешает микрофизике (квантовой механике) быть наукой столь же объективной, достоверной и практически полезной, как и макро физика.

Понятно, что элементарный этап наблюдения является процессом, поскольку в нем речь идет об элементарных событиях системы трех разных объектов ,  и , в то время как излучение и поглощение сигнала  являются процедурами. Для большей объективности наблюдения – неза­висимости его от того какой сигнал на различных этапах выбирают разные субъекты для наблюдения за изменениями объектов, необходимо всегда считать сигнал универсальным. Т.е. не только одинаково влияющим на процессы наблюдения (идеальный вариант был бы, если бы сигнал вообще не влиял, правда, при этом он не должен быть физическим объектом), но и позволяющим определять значе­ния удаленностей любых пар объ­­ек­тов, имеющих какие угодно значения характеристик – от бесконечно малых до бесконечно больших. Ниже будут сформулированы требования к универ­саль­ному сигна­лу, существование и использование которого ниже всегда предполагается, и указан реальный физический объект, кото­рый может быть при­нят в качестве сигнала при идентификации других физических объектов. Постули­рованием существования такого универсального сигнала (единственности значений его характеристик), обеспечивается возможность однознач­ного определения ха­рактеристик физических объ­ектов, необ­хо­димая для коррек­тного аксио­ма­ти­че­­с­ко­­­го построения физики. Поскольку фиксировать можно только акты излуче­ния и поглощение сиг­­­­на­­ла (но не существование его вне связи с этими актами, о чем подробнее говорится ниже), то наибо­лее просто упо­рядо­чение этапов наблюдения реализуется, если на каждом из них использовать только один и тот, же сигнал. Т.к. с мо­мен­та начала и до окончания каждого этапа наблюдения за объектами сигнал не фиксируется, а, следовательно, и сами объекты не наблюдаются, то естествен­но прини­мать, что при элементарном наблюдении они не меняются, т.е. характеристики объектов со­хра­няют свои значения. На это указывал, в частности, еще Г. Лейбниц: «Движе­ние име­ется лишь там, где происхо­дит доступ­ное на­блюдению изменение; там же, где изме­нение нельзя установить пу­тем наблю­де­­ния, там нет и никакого измене­ния», см. [6]. По­этому лю­бые наблюдаемые из­ме­не­ния объектов (их характеристик), которые могут быть зафиксированы толь­ко по завершении соответствующих этапов, воз­можны не менее чем на конечные значе­ния выше названные квантами, а количественное значение  какой-либо характеристики объекта можно определять счетным числом ее квантовых изменений или квантов, составляющих этот объект. Отношение величины  (ее значения) к своему кванту, обозначаемому , будем называть разрешающей способностью этой величины или мерой разрешения ее, и обозначать .  Можно, говорить, что мера указывает во сколько раз величина больше своего кванта. Поскольку , то для численных значений меры имеют место следующие ограничения  . Не трудно убедиться, что сопоставлять друг с другом разные значения одной и той же характеристики, и даже значения качественно разных характеристик более целесообразно путем сопоставления их мер, поскольку это имеет больший физический смысл, и более информативно, чем традиционное сопоставление абсолютных значений характеристик. В частности, если меры разрешения двух величин прямо пропорциональны друг другу, то это эквивалентно степенной связи этих величин, а степень этой связи равна коэффициенту пропорциональности мер. Если коэффициентом пропорциональности двух мер является не  константа, как в выше приведенном примере, а одна из этих величин, то это эквивалентно экспоненциальной связи этих двух величин, а степень связи равна соответствующей величине. Если меры разрешения двух величин обратно пропорциональны одной из этих величин, то это эквивалентно тому, что эта величина является натуральным логарифмом другой величины. Соответствующие соотношения между мерами разрешения имеют место и для других функциональных зависимостей величин, например для тригонометрических зависимостей. Подробнее об этом см. [7].

Под непрерывным наблюдением объекта – наблюдением изменения величины хотя бы одной из его фундаментальных характеристик   (напомним, что три фундаментальные характеристики связаны между собой) будем понимать такое наблюдение, при котором значения этой характеристики фиксируются последовательно на всех соседних этапах наблюдения, осуществляемых с помощью универсального  сигнала . Под соседними этапами такого наблюдения понимаются такие два этапа (при этом один из них пред­шествует другому),  для которых не существует этап наблюдения предшествующий одному из них, и которому предшествует дру­гой из этих этапов. Если такой этап удается зафиксировать, то это значит, что эти предшествующие друг другу два эта являются соседними к найденному этапу, но не друг к другу. Значения, опре­де­ленные на соседних этапах называются со­седними значениями, а изменение на таких этапах будем называть непрерывным изменением. Если некоторые соседние значения по тем или иным причинам не фиксируются (не фиксируются значения достоверно известные, или хотя бы предполагаемые, как соседние), то такое наблюдение ее будем считать дискретным. Две величины  и  будем называть зависящими друг от друга или связанными друг с другом, если одна из них является причиной или следствием другой что означает, кроме всего прочего, чередование этапов наблюдения за ними. В случае если наблюдение представляет собой математическую процедуру, а не физический процесс, т.е. осуществляется вне времени и без изменений в пространстве, то эти величины считают связанными функциональной связью друг с дру­гом или функционально зависимыми. Одну из этих величин, являющуюся следствием, называют функцией или зависимой переменной и обозначают , а другую , являющуюся причиной называют аргументом или независимой переменной. Знание аргумента всегда предшествует знанию функции. Связь между величинами бу­дем счи­тать непрерыв­ной, если вследствие непрерывного изменения одной величины имеет место непре­­рыв­ное изменение связанных с ней ве­личин. Отношение соседних кван­тов двух величин имеющих причинно-следственную связь (функционально связанных между собой), будем называть  скоростью изменения или производной соответствующей величины  по величине и обозначать:

            (1)

В математике эту процедуру называют дифференцированием, а обратную (симметричную) процедуру, т.е. процедуру восстановления величины  в каком-то диапазоне изменения ее  по производной, называют интегрированием,  и обоз­на­­чают . Симметрич­­ность этих двух процедур состоит в том, что они взаимно обратимы, т.е. имеют место равенства:

_,                     (2)

где   - значение величины  в начале указанного диапазона, в котором необхо­ди­мо выпол­нить интегрирование. Это значение надо при­бавлять к результату интегри­ро­вания в этом диапазоне, для того чтобы получить величину  в конце диапа­зона, т.к. само интегрирование дает лишь приращение значения величины на этом диапазоне. Отметим, что в частном случае связи величин  и , когда при различных зна­чениях  вели­чи­на сохра­няет свое значение , производная такой постоянной величины формально не существует, т.е. нельзя выполнить дифференцирование. У постоян­ной величины нет состав­ля­ющих её квантов, т.к. она сама один квант, и произ­водная дол­ж­на равняться нулю, впрочем, как и интегрирование нулевых значений. Имен­но поэтому первое слагаемое левой части (2) является начальным значением, совпадающим с самой постоянной величиной, для которой и имеют место соотношения:

 и, т.к.

Как указывалось выше, в зависимости от практической возможности или необходимости субъектом может быть установлена различная степень (порядок) предшествования друг другу состояний объектов. Применительно к квантам это эквивалентно тому, что величины их можно в указанных случаях считать состоящими из своих квантов, а последние – из своих и т.д. Понятно, что в этих случаях алгоритмы (1) и (2) можно применять соответствующее число раз. При этом мож­но говорить, что для величины  можно выполнить n-кратные диф­фе­рен­цирование и интег­рирование. Обозначения их имеют вид:

;

.

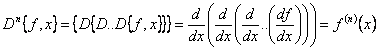Формулы для выше введенных процедур дифференцирования и интегрирования различных функциональных зависимостей легко могут быть получены с использованием выше определенного понятия меры разрешения величин, см. [7]. При выводе этих формул, которые идентичны соответствующим зависимостям для классических математических функций, можно оставаться в рамках арифметических операций и не нужно прибегать к использованию таких доволь­но не простых для осмысли­вания поня­тий классической математики как «пере­менная бесконечно малая»  величина и «предел» функций.

Обобщим формулу (2) на случай n-кратных итераций, т.е. выполним n-кратное интегрирование в диапазоне  n-кратно продифференцированной функции. Для этого на каждой итерации достаточно использовать лишь соотношение (2), а также формулы дифференцирования и интегрирования только степенной функции. В      результате получим следующее выражение, называемое формулой Тейлора:

            (3)

Правая часть этого равенства состоит из суммы двух частей. Первая из этих частей называется многочленом Тейлора степени  для функции . Это приближенное значение функции, определяемое значениями производных ее в начале диапазона, самим диапазоном и принятым порядком дифференцирования и последующего интегрирования данной функции. Вторую часть называют остаточным членом такого ряда. Чем выше принятый порядок дифференцирования и последующего интегрирования, тем точнее приближенное значение и тем меньше остаточный член. В частности, если порядок  равен максимально возможному для функции, то вторая часть равна нулю. Это означает, что данная функция может быть представлена степенным многочленом порядка . При самой низкой кратности  = 1 точность приближенного значения самая низкая, и значение не меняется с изменением , т.е. приближенное значение совпадает со значением, которое имела функция в начале диапазона интегрирования. Формулу (3) можно интерпретировать как процедуру, позволяющую осмысливать и определять (уточнять) аналитическую связь между собой двух величин. Эта процедура представляет собой предварительное дифференцирование, а затем соответствующее число раз интегрирование этой связи. В практическом естествознании поступают аналогичным образом, если хотят более точно идентифицировать какой-то объект или понятие – определить его свойства. Для этого вначале стараются как можно детальнее «расчленить» (разъять) на составляющие его части, а затем, после изучения их – «сочленить» (синтезировать) эти части в единое целое, в чем и состоял философский метод Декарта. Повторим еще раз, что степень детализации определяется субъектом в зависимости от его возможности или необходимости идентифицировать исходный объект.

Будем говорить, что объекты изменяются пространственным, вре­мен­ным или материальным образом друг относительно друга, если изменяются  соответствующие фундаментальные характеристики самих объектов а, следовательно, и соответствую­щие удаленности объектов друг от друга. Степень изменения объектов указывается значениями производных характеристик этих объектов, которые согласно (1) представляют собой отношения квантов их. Квантами являются разности со­сед­них значений характеристик, определяе­мые при непре­рыв­ном наблюдении за измеримыми/конечными объектами. Поскольку пространственная, вре­менная и материальная характеристики объектов функционально связаны меж­ду собой, то в качестве независимой переменной можно принимать любую из них. Следуя тради­ции, примем независимой переменной временную характеристику, и будем говорить, что любые относительные измене­ния физических объектов и их взаимных удаленностей обязательно происходят временным образом – во времени. Здесь время представляет собой характеристику только наблюдаемых объектов (временную удаленность их), и эта характеристика не связана с другими ненаблюдаемыми объектами или с чем-либо другим, в отличие от традиционного осмысления этого понятия как абсолютного и единого для всех, и даже для ненаблюдаемых объектов. Тем ни менее, такое понятие времени тоже позволяет ввести и однозначно осмыслить понятия «прошлое», «настоящее» и «будущее», как это имеет место в эмпирической физике. Будем называть одно из двух состояний системы наблюдаемых объектов прошлым, настоящим или будущим относительно другого состояния в зависимости от предшествования временных характеристик этих состояний друг другу. Состояние, временная характеристика которого предшествует (в соответствии с выбранным «направлением» для рассматриваемых состояний) временной характеристике другого состояния, назовем прошлым, а состояние, которому предшествует какое-то состояние, назовем будущим относительно друг друга. Если указанное предшествование невозможно установить, что эквивалентно отсутствию его, то оба состояния будем называть настоящими, а изменения объектов одновременными друг относительно друга. В соответствии с правилом упорядочения, если какое-то состояние является прошлым, настоящим, или будущим относительно иного состояния, которое в свою очередь является соответственно прошлым, настоящим или будущим относительно третьего состояния, то оба два первых состояния являются прошлыми, настоящим, будущим относительно этого третьего состояния. Пользуясь этим, можно установить предшествование во времени любых двух физических состояний одной и той же системы объектов и различных, но смежных систем физических объектов, имеющих не менее одного общего объекта. При этом не нужно считать, что существует «единое – абсолютное время», как это принято классической физикой. Принципиально подчеркнуть еще и то, что сформулированные понятия прошлое, настоящее и будущее являются субъективными, поскольку определяются субъектом в каждом конкретном случае как процесс и всегда лишь для двух определенных состояний системы. Гносеология такого субъективизма связана в своей основе с исходным субъективизмом, имевшим место при определении понятия объект (явление, событие, процесс и т.п.) как нечто, что только субъект может идентифицировать относительно других объектов. Напомним, что в традиционной эмпирической физике понятия прошлое, настоящее и будущее, считаются полностью объективными и абсолютно независимыми от наблюдаемого субъекта, поскольку определение этих понятий не связано непосредственно с отдельными субъектами. Определения таких состояний в эмпирической физике являются процедурой применимой сразу ко всем объектам и явлениям, поскольку в эмпирической физике постулируется существование единого пространственно-временного континуума. Временные соотношения между состояниями систем большого числа объектов, и даже всей вселенной в целом, т.е. отнесение состояний к прошлому, настоящему или будущему, осуществляется в эмпирической физике исходя из степени так называемой «упорядоченности» или «хаотичности» этих состояний. Руководствуются при этом вторым началом термодинамики, которое утверждает, что состояние изолированной системы объектов, является прошлым относительно другого состояния этой системы, если оно более «упорядочено», т.е. считают, что с течением времени состояния таких систем становятся более «хаотичными». Вопреки широко распространенному мнению о том, что такое отнесение состояний во времени считается объективным оно, строго говоря, таковым не является, поскольку само понятие «упорядоченности» или «хаотичности» поведения объектов является субъективным (зависящим в каждом конкретном случае от субъекта) и во многом интуитивным понятием. Состояние считающиеся «хаотичным» для одного субъекта может считаться «упорядоченным»  для другого субъекта или даже для одного и того же субъекта на разных этапах познания этого состояния. Примером могут служить письменность или речь иностранца, пока они не изучены, не говоря уже о различных криптограммах и шифрованных сообщений, код которых еще не раскрыт. Такую же субъективность можно соотносить и с проявлением случайности, которую, строго говоря, можно считать таковой, пока не удастся установить «закономерность этой случайности».

Таким образом, понятие время является субъективным понятием, но никак не объективным и независимым от конкретных субъектов, как это традиционно принято. Прав был русский философ П.Я. Чаадаев, говоривший, что «Все времена мы создаем сами, в этом нет сомнения, бог времени не создал, он дозволил его создать человеку», см. [8] стр. 621. И, исходя из такого «дозволения», у различных людей и даже сообществ существуют различные восприятия времени, и они существенно отличаются от восприятия принятого в традиционной эмпирической физике. Так, имеются народности (племена) не знакомые с традиционной физикой, которые в своей повседневной жизни обходятся принципиально иным осмысливанием последовательности и продолжительности событий. Вот что по этому поводу пишет в своей книге «Парадоксы науки» А. Сухотин, см. [9]:  «Европейские языки, например, имеют два больших класса слов: существительные и глаголы. Соответственно это вещи и процессы. Однако в некоторых языках, например у индейцев нутка, все слова соотносимы с нашими глаголами, то есть выражают действие. Скажем, понятие «волна» или «молния» у нас – существительные и обозначают вещи, а у нутка – глаголы. Они выражают движение и процессы. Сообразно этому люди нутка видят и окружающую действительность. Или же, ... есть языки, в которых отсутствует категория времени. Так, у индейцев хопи (США) нет временных понятий. В частности, они не говорят «пять дней». Хопи скажет: «Я был на охоте до шестого дня», или: «Я вернулся с охоты после пятого дня». Иначе сказать, в этом языке не используется выражение длительности. Вместо нее просто отмечают начало или конец чего-либо, не само временное протекание процесса, а его границы». В аксиоматической физике тоже не используется понятие «длительность» и введенное еще Ньютоном понятие «абсолютное время», а исходят из понятия предшествования друг другу конкретных объектов (событий, явлений, процессов и т.п.). Обобщая, можно сказать, что субъективным является и само естествознание, поскольку оно создается субъектами исходя из своих возможностей и потребностей, и в случае изменения последних парадигма естествознания может меняться, в том числе и принципиальным образом, как это имело место в прошлом, и не исключено – в будущем. Примерами изменений в прошлом парадигмы физики являлись переход от физики Аристотеля, в которой считалось, что сила вызывает изменение положения материального тела (изменение нулевой степени удаленности), к физике Галилея/Ньютона, согласно которой сила вызывает изменение скорости движения тела (изменение первой степени удаленности). А затем переход и к физике Эйнштейна (к общей теории относительности) согласно которой движение материального объекта обусловлено непосредственно кривизной пространственно-временного континуума, а не действием других материальных объектов, хотя последние и влияют на эту кривизну.

Три фундаментальные характеристики физического объ­екта можно представлять коорди­натами его в трех­мерном «характеристическом прост­ранстве». Это прост­ранство явля­ет­ся логически мыслимым («пространством представлений» по терминологии А. Пуанкаре)  и, следователь­но, оно никак объективно не влияет на физические объекты и не испыты­вает никакого влияния их. Отличается оно от пространств Евклида и Минковского тем, что все три координаты имеют различный физический смысл (характеризуют качественно различные свой­­­ства объектов) и не могут быть независимыми друг от дру­га. Точкой такого трехмерного пространства будем называть три свя­зан­ных между собой вещественных числа  представляющих трехкомпонентную сис­те­му фундаментальных характеристик объекта. В соответствии с этим термины «точка» и «объект» далее будем рассматривать как эквивалентные, если иное специально не оговорено. С учетом всего выше изложенного, и применяя идеологию и даже терминологию геометрии, удается построить физику аксиоматически, и при этом использовать только ранее приведенные физические понятия и объекты. Дадим определения еще и понятиям прямая, треугольник и окружность, неоднократно используемым в дальнейшем. Заметим, что в математике эти понятия являются частным случаем понятия «линия», формулировка которого является довольно не простым делом, на что указано даже в таком авторитетном источнике как «Математическая энциклопедия», см. [10], т.3 стр.382:  «Линия – геометрическое понятие, точное и в тоже время достаточно общее определение, которого представляет значительные трудности и осуществляется в разных разделах геометрии различно».

Бу­дем говорить, что две точки однозначно определяют единственную прямую, а три точки – определяют единственные треугольник или окружность, на которых естественно могут лежать и большее число точек. Допустимо говорить, что все эти точки лежат соответственно на прямой, на треугольнике или окружности и говорить, что прямая, треугольник или окружность проходят через эти точки. Каждая прямая, треугольник или окружность имеют в рассматриваемом трехмерном «характеристическом пространстве» три «проекции»: пространственную, временную и материальную, но ниже если это специально не оговорено, то речь идет только о пространственных «проекциях». Три точки ле­жат на одной прямой, если удаленность какой-нибудь пары их равняется сумме удаленностей двух других их пар. Способ определения пространственной удаленности двух точек друг относительно друга будет указан ниже после того, как будет  определено понятие наблюдения за физическими объектами. Часть прямой лежащей между двумя точками M  и Q будем называть отрезком, а пространственную удаленность их   будем называть расстоянием между точками или длиной этого отрезка. Любые три точки m, M, Q не лежащие на одной прямой идентифицируют плоскость и расположенный в ней треуголь­ник , представляющий собой систему трех отрезков определяемых тремя парами этих точек, каждая из которых имеет одну общую точку, называемую вершиной треугольника. Понятно, что в треугольнике имеются три вершины и при них три внутренних угла обозначаемых ниже  величины, которых однозначно связаны с размерами трех сторон (отрезков) его ниже приведенными соотношениями (4). Углы указывают пространственные направления друг относительно друга двух прямых лежащих в одной плоскости или двух плоскостей, если два треугольника, имеющих общую строну, лежат в разных плоскостях. Заметим, что идентификация треугольника – определение каждого из трех размеров сторон и углов его является одной процедурой, а не тремя различными процессами, предшествующими друг другу.  Три точки лежат на одной окружности, если сумма квадратов удаленности каких-нибудь двух пар этих точек равна квадрату удаленности третей пары их, называемой диаметром окружности. Уточним, что это условие является лишь достаточным и не является необходимым для принадлежности трех точек одной окружности.  С учетом принятых определений, прямую и отрезок можно называть незамкнутыми линиями, такими у которых начало и конец линии пространственно не совпадают друг с другом. Окружность и треугольник являются замкнутыми линиями, такими у которых начало и конец совпадают друг с другом, и поэтому любая их точка может быть принята за начало или конец. У прямой начало  и конец удалены друг от друга на бесконечно большое расстояние, у отрезка – на конечное расстояние, а у треугольника и окружности – на бесконечно малое расстояние. Рас­стоя­ния между объекта­ми, являю­щи­мися состав­ны­ми частя­ми одного и того же объекта, называются раз­ме­рами его. Таким образом, используя понятие про­ст­ран­ст­венной удаленности, можно однозначно осмыслить и опреде­лить количественно и качественно такие понятия как прямая, треугольник, окружность, углы, относительные пространственные направления прямых и плоскостей, а также следующие, свя­занные друг с другом понятия. Такими понятиями являются распо­ло­­­жение точки, не лежащей на прямой по отно­шению ней; расположение точки вне плоскости по отно­ше­­­нию к ней; упорядочение располо­же­ния трех и более точек, не принадлежащих одной прямой. Каждое из этих понятий имеет только два зна­чения, которым будем при­пи­сывать знаки « + » или « – »  и соответственно называть: «слева» или «справа» от пря­мой; «над» или «под» плоскостью; «по» или «против» часовой стрелке распо­ло­жены (упо­рядоче­ны) три точки. Связь этих понятий между собой проявляется в том, что при изменении зна­ка одного понятия меняется знак дру­го­го понятия, как это показано ниже.

Для любого треугольника имеют место следующие экспериментально подтверждаемые соотношения между размерами трех его сторон  и его углами. Эти соотношения состоят в том, что размер каждой из сторон треугольника равен сумме размеров двух других сторон его, нормированных коэффициентами, называ­е­мы­ми косинусами углов между этой стороной и соответствующими сторонами. Численные значения любого из трех этих коэффициентов обозначаемых ,  и  не превосходят по модулю единицы, и они являются математическими функциями, описывающими так называемые периодические процессы – процессы при которых происходят чередования увеличении и уменьшения в ограниченном диапазоне количественных значений величин. Указанные соотношения имеют вид:

  (4)

Физический смысл этих соотношений можно интерпретировать как выражение непрерывности «характеристического пространства», в котором возможно существование треугольника как единого объекта, а не только как системы трех несвязанных друг с другом отрезков, т.е. возможна процедура идентификации треугольника. Если один из коэффициентов равен нулю, например =0, то сумма квадратов двух других коэффициентов равна единице. Угол соответствующий нулевому коэффициенту равен  или  и называется прямым, а треугольник, имеющий такой угол, называется прямоугольным. Все три точки m, M, Q такого треугольника, называемые вершинами треугольника, лежат на одной окружности. Отрезок MQ является диаметром этой окружности – наибольшим отрезком, соединяющим две точки окружности. Если один из коэффициентов равен минус единице (угол соответствующий ему равен 180⁰ или ), то два других коэффициента равны единице (соответствующие им углы равны нулю). Это соответствует выше указанному случаю, когда треугольник вырождается в прямую.  Произведение отрезка (его длины) на косинус угла между ним – и другой прямой называется проекцией отрезка на соответствующую прямую. С учетом этой терминологии, можно говорить, что сторона треугольника равна сумме проекций на нее двух других сторон. В прямоугольном треугольнике квадрат размера стороны, лежащей против прямого угла и называемой гипотенузой (как указывалось выше, она является диаметром окружности, на которой лежат все три этих точки), равен сумме квадратов размеров двух других сторон треугольника называемых катетами. Это соотношение называется теоремой Пифагора. Справедливость указанных выше соотношений для квадратов косинусов углов и размеров сторон прямоугольного треугольника легко может быть прослежена исходя из равенств (4). Действительно, подставляя в правую часть первого из этих равенств значения для размеров сторон из второго и третьего равенств (с учетом =0), получим первое из выше указанных соотношений для квадратов косинусов углов. Умножая второе равенство на , а третье равенство на  и складывая эти произведения, получим (с учетом первого равенства) теорему Пифагора. Заметим, что выше полученные для прямоугольного треугольника соотношения применяются для практических  вычислений самих углов и косинусов их с использованием размеров сторон треугольника.

Можно сказать, что соотношения (4) являются фундаментальным законом, и мы в дальнейшем будем неоднократно его использовать. Объект, состоящий из трех материальных тел, которые можно идентифицировать относительно и с использованием друг друга, будем называть простейшим материальным телом. Согласно (4) изменение пространственной удаленности одной пары объектов составляющих такое тело может повлечь за собой изменение удаленности и двух других его пар. В этом случае материальное тело будем называть деформируемым или упругим -  способным  изменять свои размеры. Если в простейшем теле изменения удаленности двух составляющих его объектов не вызывают изменение удаленности каждого из них до третьего объекта называемого центром (например, это может иметь место, если два объекта находятся на окружности с центром в третьем объекте), то такое тело называется недеформируемым или твердым телом. Можно говорить, что в простейшем теле центр его является изолированным от двух других его тел. Пространственная удаленность друг от друга таких твердых тел определяется удаленностью их центров, а для упругих тел необходимо знать удаленности всех составляющих их объектов. Физические объекты, у которых любые три пары составляющих их объектов являются упругими или твердыми телами, называют соответственно упругими или твердыми телами. Физические объекты, с которыми практически имеют дело, являются упругими. Твердыми телами теоретически можно считать лишь все составные части простейших физических объектов.

Далее более подробно обсуждается вопрос лишь об относительном движении объектов – изменении расстояния (пространственной удаленности) хотя бы между двумя из трех всегда существующих объектов как функции времени (их временной удаленности), т.к. в соответствии с традицией это представляется ключевой проблемой физики и естествознания в целом. Ниже указано, что каждые два объекта могут совершать два качественно отличающихся друг от друга движения – радиальное и тангенциальное. Заметим, что, рассуждая аналогично ниже изложенного, можно анализировать зависимости и других пар фундаментальных характеристик объектов связанных, как указывалось выше, между собой. Для любого физического объекта всегда существу­ют такие другие объ­ек­­ты (по крайней мере, существует один), относительно которых возможно изменение (движение)  этого объекта. Действительно, абсолютное отсутствие возможности изменений объекта относительно каких-либо других объектов означало бы невозможность наблюдения за ним, что эквивалентно отсутствию самого этого объекта. Ясно, что в силу функций выполняе­мых сигна­лом, нельзя фиксировать отно­ситель­­ное движение двух объек­тов, одним из ко­то­рых является сиг­нал. Это связа­но с тем, что определять изменение расстоя­ния между объектами а, следовательно, наблюдать от­но­си­тель­ное движение их, можно лишь с помощью сигнала и, следо­ва­­тель­­­но, толь­ко для пар объек­тов, ни один из которых не является сигналом. Поскольку фиксировать мож­но лишь излучение и поглощение сигна­ла, но не сам сигнал вне связи с этими событиями, то по­ня­тие движения сигна­ла  и все его кинематические параметры, могут быть введе­ны только относительно двух других объек­тов M и m, излучающих и поглощающих его. Формально можно счи­тать, что  при излуче­нии и при поглощении сиг­нала он удален  соответствен­­­но от объек­та поглощения и от объек­та излучения на величины удаленностей этих двух объек­тов друг от­ дру­га. Эти две удаленности не состоят из нескольких частей опреде­ля­емых в результате последовательных актов наблюдения, а определяются одним этапом наблюдения, в котором имеют место два простейших события – излучение и поглощение сигнала. На каждом этапе наблюдения не существуют никакие другие удаленности этих объектов и поэтому можно сказать, что они являются или бесконечно малыми или бесконечно большими, т.е. они являются квантами самих себя и совпадают с текущими удаленностями объек­тов М и m. Таким образом, при излучении и поглощении сигнала имеют место следующие соотношения:  и . Как следует из выше изложенного, между  пространственной и временной удаленностью любых двух физических объектов друг от друга существует функциональная зависимость, что позволяет определить ско­рость движе­ния сигнала во времени меж­ду излучающим и поглощающим объектами. Согласно (1) эта скорость равна отноше­нию соседних квантов пространственной и временной удален­ности сигнала от каждого из этих объектов, т.е. совпадает с отно­ше­нием пространственной  к времен­ной удаленности сигнала от каждого из объектов, между которыми движется сигнал. Напомним, что с учетом ранее указанного требования объективности и универсальности наблюдений, сам сигнал должен быть универсальным. Поэтому такая скорость сигнала, обозначаемая ниже ,  долж­на быть  наи­боль­шей из относитель­ных скоростей движения любых наблюдае­мых объ­­­ектов любыми субъектами, иначе с помощью сигнала нельзя будет наблюдать объекты, относительная скорость которых больше его скорости, и такой сигнал нельзя считать универсальным. Следо­ва­тельно, скорость универсального сигнала постоян­на, и она является фундаментальной константой. Исходя из этого, формально можно счи­тать, что в промежутке между излучением и поглощением сигнала он находи­т­­ся на прямой, проходящей через эти два объекта, и распола­гается между ними, т.е. предшествует лишь одному из объектов. Таким образом, время элементарного наблюдения за двумя объектами М и m, может быть выражено через рас­стояние между объектами  и ско­рость сигнала  следующим образом:

                          (5)

Здесь и ниже для упрощения написания и восприятия формул, в которых совместно фигурируют пространственная и временная удаленности двух объектов, нижние индексы у временной удаленности опущены, чтобы не повторяться. Очевидно, что пока сигнал движется между объектами, пространственная удаленность их друг от друга может измениться на какую-то бесконечно малую величину , зависящую от удаленности этих объектов от других всегда существующих (в количестве ни менее одного) объектов. Для определения скорости такого изменения необходимо эту величину разделить на время элементарного наблюдения определяемого (5). Не трудно проследить, что при этом скорость изменения объектов будет обратно пропорциональна расстоянию между ними:

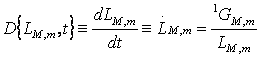       (6)

Такая зависимость относительной скорости объектов от их взаимной удаленности подтверждается опытным путем, в чем нагляднее всего можно убедиться, наблюдая, например, за движущимся относительно наблюдателя автомобилем (за любым другим объектом). Такое наблюдение может быть осуществлено или с использованием приборов, способных определять удаленности между автомобилем и наблюдателем на каждом этапе наблюдения или непосредственно самим наблюдателем. Скорость автомобиля, как ее воспринимает наблюдатель, увеличивается по мере приближения к наблюдателю и уменьшается по мере удаления от него. Принципиальное отличие таких наблюдений от показаний спидометра автомобиля находящегося внутри салона, обусловлено тем, что обычно такой спидометр показывает скорость автомобиля только относительно имеющихся под ним участков трассы, но не относительно наблюдателя, удаленность до которого меняется по мере перемещения автомобиля. Чаще всего, спидометр автомобиля показывает даже не эту скорость, а скорость вращения вала двигателя, которая может быть неоднозначным образом связана с изменением расстояния между автомобилем и участками трассы под ним. В частности, это имеет место, если автомобиль движется по скользкой или не абсолютно жесткой трассе. Зависимость (6) относительной скорости двух объектов от расстояния между ними может быть формально объяснена тем, что на каждом этапе наблюдения в качестве масштаба, используемого для сравнения изменений удаленности двух объектов, наблюдатель принимает расстояние между этими же объектами, замеренное на предшествующем этапе. Такой выбор масштаба представляется универсальным и часто единственно возможным, т.к. иной выбор, дополнительно потребует использования других объектов помимо двух наблюдаемых объектов и сигнала, доступ к которым, как правило, существенно затруднен, например, случае наблюдения за двумя объектами, находящимися в открытом море или в космосе. Но даже при наличии этих дополнительных объектов указанный выбор масштаба остается наиболее оптимальным, т.к. при использовании каких-то других объектов необходимо учитывать движение их относительно друг друга и относительно каждого из двух рассматриваемых объектов, что может принципиально усложнить определение искомой относительной скорости наблюдаемых объектов. Обратно пропорциональная зависимость скорости относительного движения двух объектов от расстояния между ними в определенной мере эквивалентна эффекту Доплера, согласно которому изменение расстояния между приемником и источником колебаний приводит к изменению скорости распространения звука (волны, или частоты колебаний его), излучаемого источником и принимаемого приемником. Выше изложенные рассуждения позволяют получить и следующие выражения для производных любого порядка от расстояния между объектами по времени, называемые кинематическими параметрами относительного движения двух объектов соответствующих порядков:

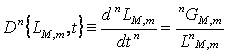                              (7)

Физический смысл величин  будет раскрыт ниже.

Соглас­но (7) при уве­ли­чении рас­стоя­ния между двумя измеримыми объ­ектами, и при прочих равных условиях, которые, как уже говорилось выше, никогда абсолютно точно не удается реализовать,  относительные ско­рость, уско­ре­ние и другие кинематические па­ра­­метры их уменьшаются, а при уме­нь­шении расстояния – эти параметры увеличиваются. Причем, чем более высокий порядок име­ют кинемати­ческие па­­ра­метры, тем быстрее про­ис­ходят их изменения. Если не учитывать возможные изменения пространственных и временных удаленностей между внутренними частями объектов (считать такие изменения бесконечно малыми), то различие относительных движений разных пар движущихся объектов, находящихся в одинаковых внешних условиях, может быть объяснено только разным числом составных частей у этих объектов.

 Следовательно, как самим объектам, так и системам их и любым частям объектов, вплоть до квантов, можно сопоставлять параметр, определяющий только различие числа составляющих частей и влияющий при прочих равных условиях на величину взаимодействия объектов. Повторим, что введение такого параметра оправдано в случае, если пространственные и временные удаленности частей внутри каждого объекта бесконечно малы по сравнению с соответствующими удаленностями между самими этими объектами, т.е. если каждый такой составной объект допустимо рассматривать не как систему, а как единый автономный объект. Поскольку изменения пространственных и временных удаленностей друг от друга внутренних частей в рассматриваемых случаях приняты отсутствующими, то упомянутый параметр, определяющий различие относительных движений (взаимодействий) разных пар таких объектов, должен быть связан только с различием материальных характеристик объектов этих пар. Этот параметр, обозначаемый ниже той же буквой что и объект, называется  массой объекта. Таким образом, введенное поня­тие массы характеризует только степень того, насколько объект яв­ляется со­став­ным, и определяется лишь числом частей (в конечном счете – числом квантов ма­­те­рии), из которых состоит объект. Т.е. физический смысл этого понятия совпа­да­ет со смыслом, который вкладывается в понятие количество материи (вещества, субстанции и т.п.), но не в понятие качество ее. Следовательно, нет необходимости приписывать мас­се никакие другие свой­ства типа: соз­давать гра­ви­тационные поля, обладать инерцией и т.п., как это делает традиционная эмпирическая физика.

В случае если два наблюдаемых объ­екта М и m изолированы от других объектов, то в соответствии с вышеуказанным свойством таких объектов сохранять свои характеристики, масса такого составного (тоже изолированного) объекта равная M+m остается постоянной, и может измениться только при изменении состояния изолированности его. Пространственная удален­ность этих двух объектов друг от друга, и диф­фе­рен­ци­а­лы всех по­рядков пространственной удаленности, могут ме­няться за элемен­тар­ные временные интервалы  только на одни и те же элементарные ве­личины. В этом слу­чае, в (7) коэф­фициент  взаимодействия двух объектов дол­жен быть постоянным и пропорциона­льным сум­ме масс взаимодей­ствую­щих объ­­ек­тов, т.е. массе составного объекта:

.

Здесь- коэффициент, который может быть назван коэффициентом автономного действия простейшего объекта единичной массы, т.е. такого действия, которое не зависит от взаимодействий любых других объектов между собой и даже от существования таких других объектов. Формально можно говорить, что автономное действие объекта это «взаимодействие» его с виртуальным «объектом», масса у которого отсутствует – равна нулю. В рассматривае­мом случае кинематические параметры относительного движения двух объектов определяемые (7) можно записать в виде суммы двух слагаемых, соответствующих автономным движениям (действиям) первого объекта относительно второго и второго относительно первого:

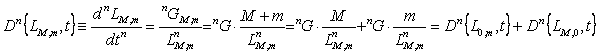(8)

Такая интерпретация не просто соответствует принятому традиционной физикой положению о сохранении пространственного направления и величины скорости авто­ном­ных движений изолированных материальных тел относительно инер­­­ци­альной системы отсчета, что является первым законом Ньютона, но и обобщает это положение на кинематические параметры любого порядка. Нетрудно заметить, что для случая , выражение (8) соответствует закону Всемирного тяготения классической физики. Далее, как видно из (8) имеет место соотношение  эквивалентное третьему закону Нью­тона о равенстве автономных действий и противодействий двух объектов. Таким образом, нет необходимости вводить понятие инерциальной системы отсчета, экспериментально идентифицировать которую принципиально нельзя, и априори постулировать законы Ньютона, поскольку их можно получать как следствия принятых исходных положений.

Относительное движение двух не изолированных друг от друга объектов М и m, но изолированных от всех других объектов, называют в эмпирической физике гравитационным взаимодействием этих объектов. Это взаимодействие двух объектов, является притягивающим, что обусловлено существованием (не равных нулю) квантов пространственной  и временной  удаленностей, и прямо пропорциональной зависимостью между ними (5), имеющей место благодаря понятию скорости движения сигнала, принятой максимально допустимой и, следовательно, постоянной величиной. Кроме того, это обусловлено еще и тем, что в качестве независимой принята временная характеристика объектов и, следовательно, знаменатели кинематических параметров, количественно определяющих взаимодействия, пропорциональны взаимной удаленности объектов в соответствующей степени, см. (7). Существуют два симметричных – качественно противоположных вида таких движений, отличающихся пространственной направленностью движения каждого из участвующих в них объектов: «друг к другу» и «друг от друга», т.е. взаимным сближением и удалением объектов. Оба эти движения является монотонными – сохраняющими свою пространственную напрвленность, что обусловлено невозможностью всех других объектов, в силу изолированности их, влиять на поведение рассматриваемых двух объектов. В силу существования горизонта, каждое из этих движений заканчивается тем, что пространственная удаленность между объектами достигает одного из двух экстремумов – минимума или максимума при которых расстояние между объектами становится соответственно бесконечно малым или бесконечно большим. Поскольку при обоих этих экстремумах относительные кинематические параметры двух рассматриваемых объектов принимают нулевые значения, то объекты при этом становятся изолированными еще и друг относительно друга, и тем самым относительно всех существующих объектов – становятся абсолютно изолированными. Это позволяет говорить, что при гравитационном взаимодействии объекты стремятся к состоянию абсолютной изолированности их. Понятно, что после достижения объектами одного из двух экстремумов относительное движение этих объектов, если и может возобновиться (появиться возможность определения относительного ускорения их), то только при движении, качественно противоположном предыдущему. Т.е. если до достижения экстремума объекты сближались, то после достижения экстремума объекты могут, лишь удаляться друг от друга, и наоборот. Таким образом, можно говорить, что гравитационное взаимодействие является проявлением стремления объектов восстановить абсолютную изолированность их, нарушение которой и является причиной возникновения гравитационного взаимодействия. Другими словами, два качественно противоположных вида относительных движения при гравитационном взаимодействии объектов могут лишь чередоваться и перемежаться состоянием абсолютной изолированности каждого из объектов, и каждое из этих трех состояний может считаться причиной или следствием других этих состояний. С учетом того, что гравитационное взаимодействие двух объектов является процессом, т.е. происходит с затратой времени, допустимо говорить, что этот качественно обратимый процесс является периодическим и что для него время обратимо. Что касается количественной обратимости таких процессов, то она имеет место, как указывалось выше, только в рамках второго приближения – приближения Галилея.

Качественное изменение гравитационного взаимодействия двух объектов, т.е. переход этих объектов в обычное взаимодействие может произойти только при уменьшении до конечной величины пространственной удаленности между каким-нибудь третьим объектом и каждым из рассматриваемых объектов. Это возможно, поскольку другие объекты (согласно определению, физические объекты существуют в количестве не меньше трех) тоже могут двигаться друг относительно друга, и могут приблизиться к рассматриваемым двум объектам на конечные расстояния. Понятно, что при качественном изменении гравитационного взаимодействия двух объектов (при этом они перестанут быть изолированными от всех других объектов) изменится аналитический вид взаимодействия таких объектов до этого определявшийся (8). Такое изменение взаимодействия объектов должно осуществляться в соответствии с соотношениями (4), определяющими значения удаленности между тремя не изолированными друг от друга объектами.

Основываясь на этих рассуждениях можно прийти к выводу, что в случаях любого счетного числа неизолированных друг от друга объектов возникновение взаимодействия их (каждой пары объектов) являются тоже следствием нарушения абсолютной изолированности объектов, а сами процессы относительных движений – это стремление восстановить ее. Понятно, что наблюдать и осмысливать поведение всех существующих в природе пар объектов, в таком же объеме как это допустимо для двух объектов, практически не возможно, и единственный выход – это наблюдать за ансамблями объектов, используя методы стохастических процессов. Именно этим и занимается получившая в последнее время развитие так называемая «Теория хаоса», некоторые положения которой изложены в интересных монографиях И. Пригожина внесшего в эту теорию существенный вклад, см. [11]. Согласно этой теории и для ансамблей может иметь место указанное выше чередование состояний изолированности и взаимодействия их между собой. Подтверждением этого является существование так называемых «химических часов», реализуемых, например, в реакции Белоусова-Жаботинского, в которой наблюдаются периодические сближения и удаления миллиардов молекул участвующих в этой реакции веществ. Ясно, что по мере увеличения числа наблюдаемых взаимодействующих объектов, уменьшается вероятность возникновения состояний их абсолютной изолированности (возможности фиксирования субъектом таких состояний), сокращается продолжительность пребывания в таком состоянии, если оно наступает, и увеличивается длительность процесса взаимодействия.

Исходя из изложенного, можно с большой степенью уверенности предположить (экспериментально проверить или опровергнуть это по понятным причинам невозможно), что поведение системы всех объектов вселенной будет происходить в качественном отношении в соответствии со сценарием гравитационного взаимодействия двух объектов. Имеется в виду, что допустимо пребывание всех объектов вселенной в двух глобальных (фундаментальных) состояниях абсолютной их изолированности, при которых они расположены наиболее и наименее компактным образом. Т.е. все объекты удалены друг от друга соответственно на бесконечно малые и бесконечно большие расстояния. Эти два состояния можно называть состояниями тепловой смерти вселенной, и они должны чередоваться с промежуточным для них состоянием, при котором объекты взаимно удалены на конечные расстояния. Это состояние, в котором находится вселенная сейчас, можно назвать состоянием жизни. До тех пор, пока не будет установлена причина существования такого чередования, т.е. пока не будет достоверно установлена возможность существование какого-то другого «метафизического» состояния, отличающегося от состояний смерти и жизни, прогнозируемый периодический процесс поведения всех объектов вселенной может считаться естественным (фундаментальным законом). Учитывая все выше изложенное, обнаружить третье упомянутое «метафизическое» состояние ни практической, ни даже теоретической надежды не существует. В настоящее время некоторые экспериментальные данные космологии позволяют предполагать, что вселенная находится в таком «состоянии жизни», когда все объекты ее, стремясь достичь абсолютной изолированности, удаляются друг от друга. Изложенные рассуждения укладываются в рамки положений, на которых основана теория о, так называемом, Большом Взрыве. Согласно этой теории современному состоянию вселенной предшествовало состояние, при котором все физические объекты (вся материя) были расположены наиболее компактным образом – были минимально удалены друг от друга. Исходя из этого, характеристики всей системы объектов можно отсчитывать от такого эксклюзивного состояния называемого «начальным». Формально можно считать, что в этом состоянии существовал лишь единственный материальный объект, из которого впоследствии возникли все другие материальные объекты. Теологи могут пытаться связывать такой единственный объект с понятием Бог-творец, часть которого имеется в каждом объекте и субъекте. Заметим, что теория Большого взрыва не рассматривает вопрос о том, что было до взрыва, и что будет после его завершения – после того, как объекты перестанут удаляться друг от друга.

Изложенное еще раз подтверждает, что существования экспериментально наблюдаемых на микроуровне дискретных изменений объектов (существования квантов энергии, массы, длины, времени и др.) лишает возможности какого-либо логического обоснования выбора математического понятия континуальность и связанного с ним понятия пространственно-временной континуум в качестве исходного понятия физики. Такой выбор был сделан на ранних этапах развития естествознания, когда существовавшие тогда технические возможности не позволяли обнаруживать дискретный характер всех физических явлений на фундаментальном уровне, и этот выбор имел цель соблюсти единообразие построения математики и физики. Это было обусловлено не только субъективными обстоятельствами, связанными с тем, что обе эти науки создавались, можно сказать, одновременно и параллельно одними и теми же учеными, но и объективными причинами. Действительно, принятые положения позволили достаточно корректно описывать поведения объектов на макроуровне единственно доступным с использованием существовавших в те времена технологий. Предположения, восходящие к атомизму Демокрита (ок. 470  до н.э.) и Лукреция (1 в. до н.э.), о том, что мир состоит из атомов находящихся в пустоте и их комбинаций долгое время оставались гениальными догадками. В дальнейшем, когда дискретность явлений стала достоверно наблюдаемой, эмпирическая физика, пытаясь хоть как-то сохранить понятие континуальность, вынуждена постулировать существование двух можно сказать качественно различных физик: макро и микро физики, для которых имеют место диаметрально противоположные закономерности. В макро физике исходят из существования непрерывных изменений объектов в пространственно-временном континууме – непрерывных изменений пространственных, временных и материальных характеристик объектов. Можно сказать, что тем самым постулируется существование и непрерывность действий объектов друг на друга или непосредственно с помощью «сил», как в механике Ньютона, или посредством «искривления» пространства, как в общей теории относительности Эйнштейна. Что касается микрофизики, то в ней тоже сохраняются представления о пространственно-временном континууме и о действиях объектов друг на друга. А для того, чтобы привести в соответствие такие представления с экспериментально наблюдаемой на микроуровне дискретностью явлений, предполагают существование каких-то носителей этих взаимных действий, которыми обмениваются физические объекты. И это, не смотря на то, что такие носители для наиболее давно известного гравитационного взаимодействия, так называемые «гравитоны», непосредственно и достоверно обнаружить, не удается. Указанное разбиение на две физики представляется в свете изложенного искусственным, т.е. обусловленным лишь неспособностью разработать единый подход к описанию поведения макро и микрообъектов в рамках принятого математического понятия пространственно-временного континуума.

Предлагаемый аксиоматический подход, в котором не используется понятие континуум, делает указанное разбиение на две физики не нужным и тем самым радикально меняет философию физики и частично всего естествознания. Проявляется это в том, что поскольку изменения объектов наблюдаются субъектом только друг относительно друга, и при этом используются лишь сами объекты, то отпадает необходимость искусственно вводить в физику представления о «силах/взаимодействиях» или «кривизне» пространственно-временного континуума, как самостоятельных и объективно существующих физических понятиях/сущностях. С помощью этих понятий в эмпирической физике делаются попытки определить внешние причины и объяснить механизмы изменений объектов. В то время как при аксиоматическом подходе вообще отпадает необходимость предполагать существование каких-либо специальных внешних причин изменений объектов, т.к. достаточно считать, что изменения объектов друг относительно друга являются естественным состоянием их, которое лишь наблюдается субъектами вышеуказанным простейшим способом – фиксированием излучения и поглощения объектов (изменений их числа на единицу). Или, говоря иначе, если и существуют причины изменений объектов, то эти причины заложены только в самих объектах, а не вне них, и скорее всего, однозначно установить механизмы таких изменений с помощью внешних объектов не удастся. Вне объектов можно и нужно выяснять лишь то, в каких случаях изменения не имеют место. Строго говоря, поскольку наблюдения любого объекта осуществляется субъектом относительно и с помощью других объектов, то это вообще не позволяет говорить об изменениях отдельных объектов, т.к. можно говорить лишь об изменениях их систем. Более того, нельзя исключать и того, что  на такие изменения влияет даже наблюдаемый субъект, например, выбором способа наблюдения или каким-то другим образом. По поводу такого влияния ведутся продолжительные дискуссии в естествознании вообще, и в квантовой механике, в частности, хотя полностью познать такое влияние субъекта (даже если допустить возможность существования его) нельзя, т.к. субъект, как указывалось выше, актуально недетерминирован.  

Как показывают экспериментальные наблюдения, в природе существуют не только гравитационные, но и другие качественно отличающиеся друг от друга взаимодействия двух объектов, например, так называемые электростатические (отталкивающие и притягивающие) взаимодействия, электромагнитные, тепловые, химические и другие взаимодействия. Отличительной особенностью всех таких взаимодействий является то, что они проявляются только в случае влияния каких-то других материальных объектов на процесс наблюдении за двумя объектами. В частности, возникновение ситуации при которой какой-либо третий объект Q становится неизолированным от двух гравитационно взаимодействующих объектов М и m, может привести к изменению такого взаимодействия между ними не только количественно, но и качественно. И даже может привести к прекращению взаимодействия между этими двумя объектами, т.е. может привести к тому, что два объекта станут изолированными друг от друга. Например, в зависимости от величины пространственной удаленности объекта Q относительно М и m, гравитационное взаимодействие этих объектов может трансформироваться в электростатическое или в электромагнитное взаимодействие. Для иллюстрации этого, и в первую очередь,  для определения понятия последних взаимодействий, необходимо предварительно уточнить определение тангенциального и радиального относительных движений объектов.

Как уже указывалось выше для трех и более объектов (а лишь в таком количестве объекты существуют в природе) относительное движение двух из них, может иметь место только при относительном движении, как минимум, еще другой пары объектов, одним из которых должен быть хотя бы один объект исходной пары. Другими словами, невозможно движение только одной какой-нибудь пары объектов, без того, чтобы в результате не реализовывалось относительное движение еще и другой смежной пары объектов, одним из которых был бы какой-нибудь объект первой пары, или – без того, чтобы не быть результатом движения другой такой смежной пары. При этом каждое из относительных движений этих смежных пар имеет место лишь в рамках одной процедуры, а не представляет собой два различных процесса, предшествующих друг другу. Невозможность относительного движения только одной пары объектов обусловлена фундаментальными соотношениями (4) (или сама обуславливает их), связывающими три удаленности между тремя не изолированными друг от друга объектами. Таким образом, принятое эмпирической физикой положение о том, что физические объекты самостоятельно обладают или электростатическими, или электромагнитными, или даже гравитационными свойствами, т.е. такие свойства существуют в объектах самостоятельно и вне связи с существованием как минимум двух других объектов, можно считать не имеющим под собой экспериментального обоснования. Такие свойства «в чистом виде» зафиксировать принципиально нельзя – они проявляются только в виде относительных движений как минимум трех объектов. Как показывают многочисленные эксперименты, ни электрические, ни магнитные заряды, ни даже гравитационные массы самостоятельно (в единственном числе) не существуют как физические объекты. Невозможно наблюдать ни появление, ни исчезновение, ни наличие только одного из этих объектов без соответственно появления, исчезновения, наличия другого физического объекта – не существуют ни гравитационные, ни электрические, ни магнитные монополи. Последним обстоятельством объясняется, в частности, то, что при возникновении электростатического или магнитного заряда одного знака возникает заряд противоположного знака.

Два объекта могут совершать два качественно отличающихся между собой относительных движения в зависимости от того, как меняется расстояние между этими объектами по сравнению с изменениями расстояний каждого из них до других не изолированных объектов. Относительное движение объектов m и М будем называть радиальным, если изменение (увеличение или уменьшение) расстояния между ними на каждом этапе наблюдения является наибольшим по сравнению с изменением расстояния каждого из этих объектов до любого другого не изолированного объекта системы. Движение объектов q и Q будем называть тангенциальным, если имеет место прямо противоположное предыдущему, т.е. имеет место наименьшее изменение расстояния между этими объектами по сравнению с изменениями расстояний их до любых других объектов, или, иначе говоря, если на каждых этапах наблюдения расстояние между q и Q остается постоянным. Траекториями радиальных и тангенциальных движений являются, соответственно прямые/радиусы, на которых расположены объекты m и М, и окружности с центрами в Q или в q и радиусом, равным расстоянию между q и Q. Говорят, что при радиальном относительном движении двух объектов остается постоянным пространственное направление движение, но максимально меняется взаимная удаленность их, а при тангенциальном движении сохраняется взаимная удаленность их, но максимально меняется пространственная направленность движения. Если имеет место радиальное или тангенциальное движение объектов М и m, и соответственно тангенциальное или радиальное движение другой пары объектов одним из которых является объект предыдущей пары M и Q или m и Q , то говорят, что прямые mM и mQ взаимно перпендикулярны. Направления радиального и тангенциального относительных движений каждой такой смежной пары объектов перпендикулярны друг другу, а направления радиального и тангенциального относительного движения разных пар этих трех объектов называют взаимно параллельными. При этом оба типа последних движений асимметричны друг по отношению к другу. Это означает, что движение одного типа какой-нибудь из выше указанных пар, например, М и m является движением другого типа смежной пары объектов Q и m, и наоборот. Скорости и другие кинематические параметры радиальных и тангенциальных относительных движений объектов, будут иметь направления движений соответствующих пар объектов и количественно определяться производными по времени от расстояний между этими объектами.

Убедимся, что описываемое эмпирической физикой поведение электрического заряда в магнитном поле, качественно совпадает с поведением обычного материального объекта m, движущегося радиально или тангенциально относительно двух других материальных объектов М или Q расположенных на взаимно перпендикулярных прямых mM и mQ. В соответствии с этим, и по аналогии с традиционным названием – электромагнитное взаимодействие зарядов назовем указанное поведение объектов m, М, Q радиально-тангенциальным взаимодействием их. При этом радиальное движение объекта соответствует электрическому взаимодействию его, а тангенциальное движение - магнитному. Аналогично указанной выше асимметричности радиального и тангенциального относительных движений, имеет место и асимметричность электромагнитных взаимодействий. В физике говорят, что электрическое взаимодействие вызывает магнитное взаимодействие и наоборот, или иначе – оба взаимодействия не могут существовать друг без друга. В соответствии с имеющим место фундаментальным соотношением (4) кинематические параметры радиального и тангенциального движений связаны между собой. Такая связь легко может быть установлена путем дифференцирования по времени соотношения, определяемого теоремой Пифагора, между катетами  и гипотенузой  прямоугольного треугольника . Указанное дифференцирование показывает, что ускорение радиального движения объекта пропорционально квадрату тангенциальной скорости его и обратно пропорционально радиусу кривизны траектории. При изменении направленности тангенциального движения (его знака)  будет меняться направленность (знак) радиального движения и наоборот. Аналогичная зависимость, как показали эксперименты голландского физика Х. К. Эрстеда (1777 – 1830) и американского физика Г. О. Роуланда (1848 – 1901), имеет место и для заряда, движущегося в магнитном поле (сила Лоренца), или для двух параллельных проводников с током, создающих магнитные поля и взаимодействующих друг с другом. Сила, действующая между двумя параллельными проводниками (относительное ускорение их), прямо пропорциональна произведению сил токов в проводниках и обратно пропорциональна расстоянию между ними. Если учесть, что под током понимается движение зарядов вдоль проводника, а сила тока пропорциональна скорости такого движения, то аналитическое описание взаимодействие зарядов аналогично существующей в кинематике связи радиального ускорения с тангенциальной скоростью.

Очевидно, что тангенциальные движения двух объектов, изолированных от всех других объектов, могут быть только с нулевым тангенциальным ускорением, поскольку изолированные объекты могут иметь только постоянные  радиальные относительные скорости. Для приближения Галилея это соответствует второму закону Кеплера утверждающему, что в процессе движения таких объектов не меняется произведение расстояния между двумя объектами на тангенциальную скорость движения одного из них относительно третьего объекта.  Для трех неизолированных друг от друга объектов тангенциальное движение двух из них связано с радиальными движениями двух других пар объектов, и поэтому возможно, что какие-нибудь два из этих объектов, удаленных на конечное расстояние могут стать изолированными один от другого. Сказанное является следствием соотношения (4) между пространственными удаленностями трех объектов, рассматриваемых как единый объект – прямоугольный треугольник. Радиальное и тангенциальное движения могут иметь каждое по две взаимно противоположные направленности, которым можно приписывать знаки «+» и «–», и называть соответственно «вперед» и «назад» друг к другу и «по часовой стрелке» и «против часовой стрелки». Радиальное относительное движение каждого из двух объектов будем называть «вперед» или «назад» друг к другу в зависимости от того, уменьшаются или увеличиваются расстояния между объектами. Тангенциальное относительное движение каждого из двух объектов будем называть происходящим «по часовой стрелке» в зависимости от того, движется ли соответствующий объект этой пары «назад» или «вперед» к какому-нибудь другому объекту системы, расположенному соответственно «слева» или «справа» относительно прямой, проходящей через этот объект и другой объект пары. В противном случае, тангенциальное движение происходит «против часовой стрелки».

Поскольку как видно из (8) кинематические параметры взаимодействия двух физических объектов зависят от масс и рас­стояния их друг до друга, то для многих целей целесообразно использовать величину, инте­г­раль­­но ха­рактеризующую эту зависимость. В качестве такой величины проще и удобнее всего взять сумму (интег­ра­л) произведений автономных действий каждого из этих объектов (каждой части/массы их) на элементарные изменения расстояния между ними во всем диапазоне изменения расстояний. Для приближения Галилея эта величина имеет вид:

   (9),

где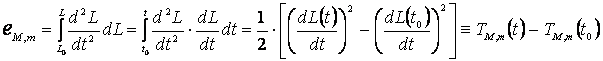 

Здесь  и   это моменты времени и соответствующие им расстояния между объектами М и m, одно из которых, например, расстояние, соответствующее моменту с нулевыми индексами предшествует другому расстоянию. Величи­ну  называют энергией системы двух объектов, приобретаемой (накап­ли­­ва­­е­мой) в ре­зуль­тате взаимодействия их друг с другом. Величины  и  мо­гут быть названы энергия­ми самих этих объ­ектов, приобретаемыми ими за тот же интервал времени в резуль­тате взаи­модействия между собой внутренних объектов составляющих их. Следовательно, энергия системы вычисляется путем сум­мирования энергий со­став­ля­ющих ча­стей. Го­во­рят, что энергия сис­темы сосредоточена в объектах, составля­ю­­щих систему, или распределена между ними. Понятно, что поскольку каждая система объектов может рассматриваться как самостоятельный единый объект, то введенное понятие энергии является фундаментальной интегральной харак­теристи­кой такого объекта (системы составляющих его объектов), в которой отражены все три фундаментальные характеристики его. Если объект изоли­ро­ван от всех других объ­ек­тов, то согласно определению этого понятия значение энергии объекта не может измениться. Это положение подтверждается экспериментально и является содержанием закона сохранения энергии. Тем са­мым не нужно при­писывать энергии различ­ные формы (гравитационную, тепловую, электромагнитную, химическую и др.) или считать ее субстанцией (?) и априори постулировать закон сохранения ее как это делается в традици­он­ной физике. Этот закон, как и все другие законы эмпирической физики, тоже является одним из следствий исходных положений принятых в аксиоматической физике.

По мере удаления объектов  и   друг от друга и от других объектов - , т.е. стремления каждого из них к абсолютной изолированности, будет иметь место со­гласно (6) и все энергии будут стремиться к  - неполо­житель­­ным минимальным значениям. При сближении объектов  и  вплоть до их объединения в единый составной объект , т.е. при   все энергии будут согласно (6), стремиться к не­отрицатель­ным максимальным зна­чениям ;  . Сле­­дова­тель­но, объект не мо­жет в резуль­тате излучения приобрести дополнительную энер­гию, а в результате по­глощения объектов потерять часть своей энергии. Наибольшую энергию сис­тема двух объектов приобретает когда , т.е. при взаимном пог­лощении объектов, начи­на­ю­­щих взаимо­дей­ст­­во­вать из состояния абсолютной изолиро­ванности - . Относительная скорость объектов в этом случае достигнет своего максимального значения , а величи­на энергии будет равна:

       (10)

Отношение энергии объекта к его массе будем называть плотностью энергии. Максимальные значения плотности энергии (до­­пусти­мые природой) и соответствующие им объекты/сос­то­я­ния будем называть фундаментальными. Как указано выше, каждый объект является составным и его можно считать состоящим из пар объектов и, следовательно, первоначально начинающимся из двух одинаковых квантов, имеющих равные массы. Поэ­то­му максимальное значе­ние энергии, которое может быть накоп­лено составным объ­ек­том массой , определяется согла­с­но (10) следующей фор­му­­лой:

                 (11)

В этой формуле, совпадающей с известной формулой теории относительности Эйнштейна, учтено, что относительные скорости лю­бых частей фундаментального объекта должны быть по определению одинаковыми и равными максимальной относительной скорости физических объектов, совпадающей со скоростью    универсального сигнала. Заметим, что в формуле (11), кроме всего прочего, нашло отражение еще и то, что согласно  (6), максимальные относительные скорости объектов достигаются при минимальных относительных расстояниях между ними. Следовательно, в фундаментальном объекте все расстояния между составляющими его частями, и размеры самого объ­­­­­­екта имеют наименьшие конечные зна­чения по сравнению с любыми не фундаментальными объектами такой же массы. Примером фундаментального объекта является нейт­рон­ная зве­­з­­­­да, плотность (отноше­­­ние массы к объе­му), и раз­меры которой равны кг/м³  и м. По­нят­но, что фундаментальны­ми могут быть только объекты, любые составляющие части которых тоже фунда­мен­тальны. Все такие объекты имеют одинаковую плотность энергии равную , а скорость погло­ще­ния и из­лу­чения фундаментальным объектом любого другого объекта тоже будет одинакова и равна . Отсюда следует, что скорости излучения и поглощения квантов материи всегда будут равны , поскольку они являются фундаментальными материальными объектами.

Необходимо иметь в виду, что согласно (6), интервал наблюдения за двумя объектами (как указано выше, он эквивалентен понятию квант временной удаленности их) связан с пространственной удаленностью объектов и в случае относительного дви­жения их такая связь влияет на саму эту удаленность. Учет этого влияния принципиален лишь в случаях, когда ско­рость  относительного движения объектов соизмерима со скоростью сигнала , и поскольку этот эф­фект эквивалентен релятивистским эффектам эмпирической физики, то он может быть наз­ван анало­гич­но. Количественно релятивистский эффект определяется ниже приведенным выражением (12), в котором удаленности на начальном и последующих этапах наблюдения обозначены соответственно  и  . Понятно, что эти удаленности тождественны между собой при 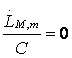, т.е. 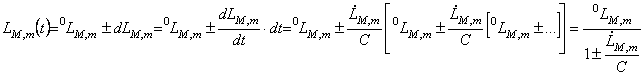при отсутствии движения объектов друг относительно друга после начала наблюдения или (что тоже самое) в случае, если скорость сигнала бесконечно велика по сравнению с относительной скоростью объектов:(12)

здесь  знаки « + » или « - » должны приниматься в зависимости от того, движется ли сигнал между двумя объектами в направлении их относительного движения «друг к другу» или «друг от друга». Понятно, что пространственная взаимная удаленность двух объектов не должна зависеть от того, на каком из них сигнал рождается, а на каком он умирает. Для того чтобы исключить такую зависимость нужно брать половину суммы результатов наблюдений этих двух вариантов. К тому же, исходя из практической возможности наблюдателя, осуществлять процесс наблюдения, сигнал всегда должен излучаться одним из наблюдаемых объектов и поглощаться им же после «отражения» (процедуры поглощение/излучение) от другого объекта, что как раз и соответствует реализации этих двух вариантов. При этом имеет место соотношение:

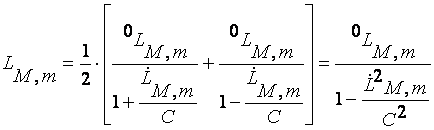                  (13)

Как нетрудно заметить, эта формула отличается от известных зависимостей теории относительности для движущегося объекта отсутствием радикала в знаменателе, что сказывается на количественном различии получаемых с их помощью результатов, хотя в качественном отношении они приводят к одинаковым эффектам. Анализ решения известной проблемы перигелия Меркурия, см. [15], во многом благодаря которой теория относительности получила признание научного сообщества, показывает, что применение формулы (13) в этом случае дает лучшие приближения к наблюдаемым результатам, чем это имеет место при использовании зависимостей  теории относительности.

Поскольку автономные движения любого объекта не зависят от существования других объектов и согласно (8) пропорциональны своей массе, то кинематические характеристики трех пар объектов M, m, Q и расстояния между ними  связаны между собой следующими соотношениями. В этих соотношениях учитывается различие пространственных направлений радиальных относительных движений объектов по аналогии с тем, как это сделано в соотношениях (4):

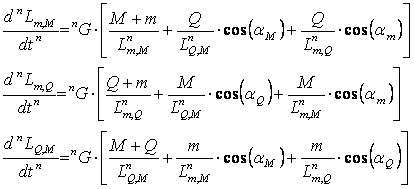         (14)

С учетом соотношений (4) связывающих между собой размеры сторон треугольника и косинусы его углов, соотношения (14) представляют собой полную систему трех дифференциальных уравнений для определения трех неизвестных – расстояний  между каждыми двумя из трех объектов. Несложный анализ этих соотношений показывает, что взаимодействия одной пары объектов будут качественно симметричны взаимодействиям двух других пар их, т.е. если взаимодействия двух пар объектов будут взаимно притягивающими, то взаимодействие третей пары будет отталкивающим и наоборот. Наиболее очевидно это проявляется в случае взаимодействия трех объектов расположенных на одной прямой. Действительно, в случае, если объект  m находится между объектами M и Q, то подставляя в первое соотношение (14) равенства , получим:

         (15)

Понятно, что в зависимости от знака фигурных скобок в (15) взаимодействие М с m будет отталкивающим (при знаке минус) или притягивающим (при знаке плюс). Если еще и , то это взаимодействие будет обратно пропорциональным расстоянию между объектами в соответствующей степени n. Такое взаимодействие называют электростатическим. В зависимости от значений  это взаимодействие может количественно соотноситься с гравитационным взаимодействием, в том числе и превосходить его в довольно широком диапазоне, включая и диапазон 10⁴², экспериментально наблюдаемый для элементарного заряда. В соответствии с ранее указанной аналогией в поведении зарядов в магнитном поле и обычных материальных объектов M, Q и m, на эти объекты можно смотреть, как на электрические заряды, которые могут одновременно появиться, или исчезнуть (как заряды, но не как физические объекты), т.е. перераспределиться. Объекты M и Q можно считать зарядами противоположных знаков, а объект m - зарядом, знак которого совпадает с зарядом М и противоположен заряду Q или, наоборот, в зависимости от взаиморасположения объектов. Поскольку относительные скорости объектов не могут превышать скорость универсального сигнала, то и скорость движения зарядов, т.е. скорость протекания тока (да и скорость любых других процессов) тоже не может превышать скорость такого сигнала. Понятно, что перераспределение зарядов вызывает перераспределение энергии между объектами, т.е. то, что в эмпирической физике называют переносом её в пространстве. В объекте, все составляющие которого изолированы от всех других объектов, сумма зарядов одного знака равна суммарному заряду противоположного знака – объект электрически нейтрален и сохраняет свою энергию. Изменить энергию или «зарядиться» (приобрести заряд одного знака) объект может лишь при взаимодействии с другими объектами. В результате обязательно должен возникнуть заряд противоположного знака. В силу того, что характеристики объектов имеют нижние пределы – кванты значений, то имеет нижний предел и величина заряда – элементарный заряд.

Понятно, что для получения количественных значений характеристик элементарного заряда необходимо в рамках приведенных качественных рассуждений построить соответствующую экспериментальным данным физическую модель взаимодействий всех внутренних неизолированных друг от друга микрообъектов элементарного заряда. Хотя последняя цель и не ставилась в рамках настоящей работы, но все же, здесь напрашивается следующее замечание. Как видно из выше приведенного рассмотрения взаимодействия трех объектов, превышение электростатического взаимодействия над гравитационным тем больше, чем ближе друг к другу расположены два из них и чем больше суммарная их масса по сравнению с массой третьего объекта. Таким образом, даже в рамках простейшей модели из трех объектов возможно качественное представление ядра атома как скопление двух объектов большой массы или как один объединенный объект повышенной массы, а электрон, считающийся элементарным зарядом можно представить как менее массивный и более удаленный от ядра объект. Совершенно очевидно, что рассмотрение систем объектов с большим числом их и с различными расположениями объектов друг относительно друга позволит описать любые виды взаимодействий объектов, в том числе и так называемые сильные и слабые взаимодействия. При этом не нужно наделять объекты различными, качественно отличающимися друг от друга, свойствами. Например, не нужно считать, что одни объекты могут всегда только притягиваться друг к другу, т.е. обладать только гравитационными свойствами, а другие объекты могут, как отталкиваться, так и притягиваться, с гораздо большей интенсивностью – обладать электростатическими свойствами или свойствами так называемых «сильного» и «слабого» взаимодействий. В соответствии с этим не обязательно представлять электрический ток как процесс движение вдоль проводника элементарных зарядов – «свободных электронов». Достаточно, по-видимому, ассоциировать ток с «эффектом домино», в котором роль «падающих», правильнее в этом случае говорить последовательно поворачивающихся,  элементов могут играть электрически нейтральные материальные объекты, состоящие из трех объектов расположенных в вершинах прямоугольных треугольников. Понятно, что каждый такой элемент имеет возможность бесконечное число раз поворачиваться по или против часовой стрелке, и после каждого «падения/поворота» такой элемент сохраняет возможность  осуществлять это неоднократно. Этим можно объяснить возможность сколь угодно долгого протекания тока в проводнике в двух противоположных направлениях без каких-либо структурных изменений в нем, если конечно не будет превышена критическая скорость протекании тока в проводнике (сбой последовательности поворотов элементов) приводящая к повреждению его. Разработка конкретных моделей поведения систем объектов, способных с тем или иным приближением количественно описывать различные наблюдаемые явления реальных материальных объектов, выходит за рамки настоящей работы, и может быть выполнена усилиями достаточного числа специалистов, разделяющих выше изложенную парадигму аксиоматического подхода к физике.

Убедимся, что кинематические параметры взаимодействий материальных объектов имеющих конечные размеры могут принимать тоже не более чем конечные значения. Наибольшие значения эти параметры  могут иметь лишь для двух объектов изолированных от всех других объектов, поскольку в этом случае относительное движение их обязательно монотонно, благодаря чему объекты всегда испытывают или только притягивающее или только отталкивающее взаимодействие. Эти наибольшие значения будут достигнуты в случае, если такие взаимодействия будут максимально продолжительными, что будет иметь место, если два объекта начнут взаимодействовать из состояния абсолютной изолированности – изолированности даже друг от друга, и  закончат когда пространственная удаленность их примет экстремальные значения – когда произойдет излучение или поглощение объектов друг другом. Численные значения кинематических параметров первого и второго порядка – скорости и ускорения могут быть получены пока лишь для приближения Галилея, для которого известно значение коэффициента автономного действия, называемого гравитационной постоянной м³/(кг×сек²⁾. Без принципиального ограничения общности, можно принять, что во всем диапазоне взаимодействия двух объектов и М , в том числе и когда , оба объекта можно идентифицировать, т.е. отличать друг от друга, хотя каждый из них является отдельной системой объектов. Это будет иметь место в ниже рассмотренном случае, когда один из объектов, например – , несоизмеримо меньше по размерам и массе объекта М, и оба этих объектов являются фундаментальными и, следовательно, всегда сохраняющими постоянные значения всех своих характеристик. Чтобы убедиться в том, что полученные результаты не предопределены релятивистскими эффектами, априори ограничивающими значения кинематических параметров из-за конечной скорости сигнала, проведенные вычисления выполнены без учета этих эффектов. Кроме того, чтобы оценить имеющие место влияния формы составного объекта М и распределения масс в этой форме, рассмотрены два простейших случая. В одном случае объект М принят шаром, а в другом – кубом. Оба они имеют одинаковые объемы - , равномерно распределенные плотности материи - и соответственно диаметр и ребро -. Ниже приведены выражения ,  описывающие ускорения объектов М (шара и куба) относительно объекта  удаленного на расстояние  от центров этих составных объектов. Эти выражения, полученные путем суммирования относительных ускорений всех частей этих объектов в соответствии с формулой (8) в которой принято , т.е. интегрированием по всему объему объектов М, имеют вид:

для шара: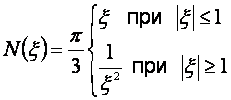    

для куба:    ,  где

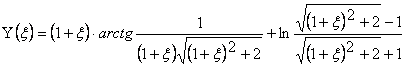
Проинтегрировав один раз уравнение (8) по времени в интервале , соответствующему начальному и текущему этапам наблюдения, получим следующее выражение для относительной скорости объектов М и :

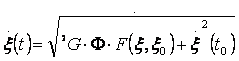,          (16)

где                          

 

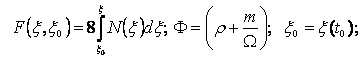
Для шара последнее выражение определяется формулой:

 

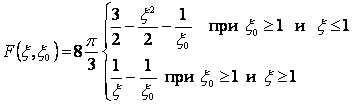
Полученные формулы показывают, что максимальные относительные ускорения объектов имеют место при  (при достижении объектом m границы объектов М). При этом выражения _, определяющие эти ускорения, принимают следующие значения: - для шара и  - для куба. Максимальные относительные скорости объектов достигаются при  и , т.е. при слиянии объектов начавших взаимодействовать из состояния бесконечной большой удаленности друг от друга. Выражения _, определяющие эти скорости, принимают значения:  - для шара и  - для куба. Учитывая, что объект m принят неизмеримо меньше объекта М, то второе слагаемое в величине  можно не учитывать ввиду малости его. Подставляя в (16) выше приведенные значения гравитационной постоянной, а также значения размеров и плотности нейтронной звезды, получим следующий диапазон значений скоростей поглощения объекта m фундаментальным шаром и кубом М  м/сек.  Эти значения с учетом принятых допущений и точности параметров нейтронной звезды, вполне соответствуют экспериментально определенной максимальной скорости объектов - скорости света м/сек. Таким образом, кванты электромагнитного излучения, частным случаем которых являются кванты света, называемые фотонами, могут быть приняты в качестве универсального сигнала, что практически имеет место не только при научных наблюдениях астрономических объектов методами радиолокации, но и при любых бытовых визуальных наблюдениях, о чем говорилось выше. Действительно, чтобы увидеть что-либо свет должен пройти путь от наблюдаемого объекта до прибора или глаза наблюдателя.

Очевидно, что поскольку любой физический объект является составным, он может считаться периодической колебательной системой. Это связано с тем, что составляющие такую систему объекты могут двигаться друг относительно друга, и в результате этого характеристики составного объекта будут меняться в диапазоне, определяемом, в конечном счете, максимальными и минимальными значениями их. Временная и пространственная характеристики такого объекта могут ассоциироваться соответственно с периодом и амплитудой (размахом) этих колебаний. Как уже отмечалось практические возможности субъектов фиксировать характеристики некоторых из таких колебательных систем, ограничены существованием горизонта. Такие ограничения проявляются в случаях, когда удаленности составляющих систему объектов становятся или бесконечно малыми или бесконечно большими. Отсюда следует, что по мере приближения к соответствующим экстремумам значения характеристик объектов становятся экспериментально определяемыми лишь с ограниченными точностями. Это, а также то, что кинематические параметры определяются итерационными процессами конечной длительности, и при этом такие процессы предшествует друг другу, соответствует соотношениям «неопределенности» Гейзенберга и «дополнительности» Бора имеющим место в эмпирической физике, и согласно которым эти параметры не могут быть экспериментально определены одновременно и с одинаковой точностью.

Наиболее явно периодичность прослеживается в поведении планет и микрообъектов. Относительные движения любых колебательных систем формально  могут рассматриваться как распространения волн материи, определяемых своими частотами, скоростью движения и энергией. В частности, как уже указывалось выше скорость излучения и поглощения квантов материи, обладающих, как и каждый материальный объект пространственной, временной и материальной характеристиками, любым другим объектом должна равняться , поскольку кванты являются фундаментальными объектами. Если колебания составляющих систему объектов происходят в одной плоскости (это, например, всегда будет иметь место, если число объектов системы не больше трех), то они называются поляризованными в этой плоскости. Поскольку согласно (7) относительные скорости объектов нелинейно зависят от расстояния между ними, то амплитуда колебаний а, следовательно, и энергия системы объектов будут зависеть от частоты колебаний системы . В первом приближении можно принимать последнюю зависимость линейной, как это и имеет место в следующем законе Планка для квантов:

,                         (17)

где  кг м² /с - постоянная Планка.

Представление о порядках значений характеристик кванта материи может дать рассмотренная выше расчетная модель двух фундаментальных объектов М и m, в которой оба этих объекта нужно рассматривать как кванты. Будем считать, что эти кванты являются одинаковыми шарами массой  радиусом , поглощение которых друг другом происходит с относительной и скоростью  при . Возводя в квадрат равенство (16) в которое нужно подставить  и  получим следующее значение для отношения размера кванта к его массе:

 м/кг,     (18)

          С учетом закона Планка (17), имеет место следующее соотношение:

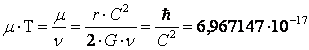кг с    (19)

Имея выражения (8) для кинематических параметров различных порядков, можно интегрируя дифференциальные уравнения, в которых используются эти выражения, получать с необходимой точностью зависимости пространственной удаленности двух объек­тов от времени. Как уже указывалось, чем выше порядок используемых кинематических параметров (чем детальнее осуществляется «расчленение» и последующее «сочленение»), тем большая точность определения таких зависимостей. Отсюда ясно, что ис­поль­зование в фундаменталь­ных законах эмпирической физики про­из­вод­ных лишь вто­рого поряд­­­­­ка от рас­­стояния по времени, можно рас­сма­три­вать как второе прибли­жение при описа­нии физи­ческой картины ми­ра, которое будем на­зы­вать физикой Галилея/Ньютона. Подходы Аристоте­ля, которыми довольствовалось человечество на ранних этапах своего развития, и в которых фи­гурировала лишь первая производная от рассто­яния по времени, поскольку считалось, что  сила вызывает лишь перемещение тел (создает скорость, но не ускорение их), можно рассматривать как первое прибли­же­ние и называть физикой Аристотеля. Если следовать Лейбницу, который рассматривал покой как предельный слу­чай движения, а не противоположность его, то ста­ти­ческое состоя­ние объек­тов, ко­торое эквивалент­но нулевой степени удаленности их друг от друга а, следовательно, и нуле­вому порядку произ­водной от расстояния по времени, мож­но рассматривать как «нуле­вое приближение». Таким образом, использование в фундаментальных закономерностях физики производных бо­лее высокого порядка приведет к более точному и полному описанию картины мира. Учитывая эмпирический характер  современной физики, а также то, что последующие уточнения являются слиш­ком малыми, чтобы быть непосредственно и повсеместно зафиксированными существующими экспериментальными технологиями (иначе это уже имело бы место), то приближения третьего и более высоких порядков еще не востребованы физикой. Понятно, что это не исключает возможность и необходимость использование более высоких приближений в дальнейшем. Можно сказать с уверенностью, что потребность в таких приближениях появится в ближайшее время, и они будут востребованы не только теорией при формулировании фундаментальных законов физики, но и использованы практикой при создании новых технологий.

Но уже сейчас имеется две фундаментальные проблемы, полностью решить которые в эмпирической физике ограниченной рамками второго приближения до сих пор не удается, и которые автоматически решается, в аксиоматической физике лишенной этих ограничений. Этими двумя проблемами являются так называемая проблема «Великого объединения» (объединение всех фундаментальных взаимодействий) – представление их как проявление одной и той же сущности, и одна из самых трудных и загадочных проблем носящая название «Стрелы Време­ни» введенное в 1928 г. известным английским физиком и астроном Артуром Эддингтоном. Суть последней проблемы состоит в следующем принципиальном расхождении между принятыми в эмпирической физике фундаментальными законами естествознания и наблюдаемым поведением физических объектов. Для всех реальных физических процессов и явлений наблюдается несимметричность последовательности выполнения их (так называемая необратимость «направления»), заключающаяся в том, что при попытках «вернуться назад» – повторить процесс в обратной последовательности (в обратном «направлении»), система не возвращается в исходное состояние. Поскольку временную характеристику объекта  мы выбрали в качестве независимой переменной, а остальные характеристики  являются функциями ее, то говорят, что для реальных процессов с участием физических объектов время всегда течет толь­ко в одном направлении – от прошлого к будущему. Говоря иначе, время является индикатором единственного направления всех изменений в природе, т.е. – индикатором того, какой из двух процессов «прямой» или «обратный» предшествует во временном отношении друг другу. Не смотря на существующую несимметричность наблюдаемых физических явлений, до сих пор в эмпирической физике считается, что все фундаментальные закономерности (аналитический вид их) для отдельных объектов обла­да­ют временной обратимостью или инвари­ант­­ностью относительно знака времени. Временная инвариант­ность на фундаментальном уровне в эмпирической физике обеспечивается тем, что в ней ограничиваются вторым приближением, согласно которому во все фундаментальные закономерности время входит только в виде второй производной от физических величин по времени, что эквивалентно тому, что дифференциал времени в знаменателях этих выражений фигурирует только в виде квадрата.

Как извест­но, любая теория, тем более фундаментальная, не может считаться правильной, если существует, хотя бы одно экспериментально наблюдаемое явление, противоречащее ей. Но поскольку имеет место противоречие не с одним, а со всеми наблюдаемыми явлениями, то эмпирическая физика предпочитает руководствоваться следующим алогичным правилом: «если теория не соответствует фактам, то тем хуже для фактов». Для объяснения и корректировки повсеместно наблюдаемой в макроявлениях необратимости используют различные искусственные рассуждения и приемы, логически не вытекающие из исходных концепций. В частности, не аргументировано изменяют дифференциальные или интегральные уравнения, описывающие эти процессы и явления, искусственно вводя в них члены с производными по вре­ме­ни нечетного порядка, или прибегают к другим искусственным приемам. При этом считают, что таким способом учитывается влияние чего-то другого (?), не рассматриваемого в данной задаче, чтобы не усложнять ее, но действующего на наблюдаемые объекты и создающего каким-то образом (?) диссипацию, приводящую к необратимости. Тем самым предполагают, что если корректно рассматривать явления, т.е. учитывать все влияющие друг на друга объекты (в соответствии с обратимыми фундаментальными законами эмпирической физики), то необратимость не имела бы место. Другими словами, считают, что в абсолютно изолированной системе объектов, т.е. в системе для которой исключено всё внешнее влияние на внутренние объекты,  необратимость не существует. Такое объяснение необратимости представляется необоснованным и неспособным решить эту проблему принципиальным образом, т.к. в реальных процессах все влияющие друг на друга объекты и явления  всегда участвуют вне зависимости от наших возможностей учитывать такое их взаимное влияние. В конце концов, природа (все существующие материальные объекты) в целом является абсолютно изолированной системой, но тем, ни менее необратимость в ней имеет место. Таким образом, принятое эмпирической физикой положение об обратимости времени в законах фундаментальных  взаимодействий и объяснение фактически наблюдаемой необратимости реальных физических явлениях влиянием не учитываемых объектов, является несостоятельным. В своей лекции по случаю присуждения в 2004 году Нобелевской Премии по физике авторитетный российский ученый В. Л. Гинзбург назвал проблему объяснения необратимости первой из «… трех «великих» проблем современной физики», ждущей своего разрешения.

Вместе с тем, очевидно, что если в соответствии с вышеприведенными возможностями аксиоматического подхода к физике не ограничиваться только вторым приближением, а использовать более высокие при­бли­жения и, следовательно, использовать производные по времени более чем второго порядка, то не­обра­тимость времени возникает уже в самих фундаментальных закономерностях. При этом отпадает необходимость искусственно вводить какую-либо причину необратимости, обусловленную существованием чего-то не учитываемого. Небезынтересным представляется мнение А. Пуанкаре, высказанное им о том, почему применение более высоких приближений для описания физических явлений вызывает отторжение его. «…В конце концов, как из всего этого видно, пришлось бы заключить, что порядок уравнений, определяющих расстояния, выше второго. Почему бы это могло смущать нас – почему мы находим вполне естественным, что ряд явлений зависит от начальных значений первых производных расстояний, и в тоже время не решаемся допустить, что они могут зависеть от начальных значений вторых производных? Это может быть только следствием известных привычек, выработанных в нашем сознании постоянным изучением обобщенного принципа инерции его следствий» (выделение моё Б.Р.), см. [3], стр.81. Надеюсь, что каждый согласится с тем, что «привычки» не могут служить надежным основанием для построения сколько-нибудь серьезной теории, не говоря уже – о построении физики, являющейся основой естествознания.

В силу малости поправок вносимых более высокими приближениями заметные проявления необратимости за счет учета таких приближений в случаях рассмотрения малого числа объектов крайне малы. Для фиксирования необратимости в таких системах объектов требуются более тщательные и длительные наблюдения, чем для систем большого числа объектов, в которых малые поправки для отдельных пар объектов «резонируют» друг с другом, накапливаются и увеличиваются, и тем самым существенно сокращается время проявления необратимости по сравнению с единичными парами объектов. Это наглядно проявляется для систем наблюдаемых объектов, как в земных условиях, так и в планетарных масштабах. Например, при проведении астрономических наблюдений за системой относительно небольшого числа доступных для наблюдения планет обнаружить необратимость существенно сложнее, чем для систем большого числа (скоплений) планет, т.к. для этого требуются несравнимо большие временные затраты, чем те, которые обычно имеют место. Можно сказать, что рост диссипации с ростом числа наблюдаемых объектов и длительности наблюдения это еще одно проявление закона перехода количества в качество. По-видимому, впервые мысль о том, что проявление необратимости времени можно объяснить неточностью фундаментальных исходных закономерностей, была высказана в 50 годах ХХ столетия известным советским астрономом Н.А. Козыревым (1908 – 1983). Но тогда эту дерзкую мысль не удалось достаточно полно, ни разработать теоретически, ни тем более обосновать экспериментально.

Как видно из изложенного, поскольку идентифицировать физические объекты – определять три фундаментальные характеристики (протяженность, длительность и материальность) можно только относительно и лишь с помощью друг друга, то отпадает необходимость использовать понятие «пространственно-временного» континуума как нечто реально существующего – способного быть хоть как-то влиять на физические объекты. В том, как понимается в эмпирической физике «пространственно-временной» континуум, как минимум одна из трех фундаментальных характеристик физического объекта, а именно – материальная, непосредственно не фигурирует даже  в названии такого континуума. Такой континуум не является физическим объектом, т.к. считается единственным и, следовательно, его нельзя идентифицировать в соответствии с определением этой процедуры для физических объектов – нельзя определить характеристики континуума путем сравнения и сопоставления с чем-либо другим. Отказ от использования в аксиоматической физике «пространственно-временного континуума» как чего-то объективно существующего обусловлен принятым определением физики как науки изучающей лишь определяемые относительно и с помощью друг друга физические объекты. Такой отказ приводит к необходимости коренным образом изменить традиционную исходную парадигму физики, согласно которой любые изменения каждого отдельного физического объекта обязательно происходят только в этом континууме и только благодаря какому-либо действию извне на этот объект. В эмпирической физике такое действие называют силой приложенной к объекту или силовым полем (иногда просто полем) действующим на наблюдаемый объект. При этом, гносеологией этого действия и его связью с другими физическими объектами, как правило, не интересуются, т.к. фактически рассматривается поведение только того объекта, на который это действие оказывается. Наиболее  всеобъемлющим и можно сказать первым проявлением такой парадигмы эмпирической физики, является положение о действии на любой материальный объект, даже сколь угодно удаленный от всех других объектов, так называемой инерции,  вызывающей один из видов движения объекта  в пространстве – движение с нулевым ускорением относительно «инерциальной системы» отсчета. Для того чтобы обосновать положение такой парадигмы о всегда имеющем место внешнем влиянии на объекты известный австрийский физик и философ Эрнст Мах (1838-1916) связывал существование инерции с влиянием бесконечно удаленных планет, и эти  взгляды Маха оказывали влияние на молодого Эйнштейна. В настоящее время многие считают, что инерция (от лат. inertia — бездействие) или инертность это внутреннее автономное свойство любого материального тела, благодаря которому оно может совершать естественное движение в пространстве, т.е. движение, совершаемое без влияния извне и поэтому сохраняющее все свои характеристики (направление, скорость и ускорение). Фактически в эмпирической физике считается, вопреки приятой в ней парадигме взаимодействия, что гравитационные, электростатические, магнитные и другие свойства объекта, как и в случае с инертностью тоже, присущи ему самому. Другими словами считается, что эти  свойства имеют внутренний автономный характер и непосредственно не зависят от действия и даже существования других объектов, хотя и проявляются только при наличии других аналогичных объектов. Во всяком случае, убедительных и экспериментально обоснованных аргументов опровергающих автономность самих этих свойств – независимость их от других объектов, с помощью которых эти свойства только и можно обнаружить, пока не существуют, по крайней мере, в отношении гравитации. Это противоречие эмпирической физики является фундаментальным, и в рамках парадигмы эмпирической физики не подающимся до сих пор разрешению, не смотря на неоднократные и давно продолжающиеся попытки его снять. Очередную попытку планируется предпринять в следующем – в 2008 году, в ЦЕРНе (Женева), где будет запущен новый ускоритель — Большой адронный коллайдер (Large Hadron Collider, LHC). Можно надеяться, что эта попытка еще больше проявит необходимость смены парадигмы традиционной физики – переход от эмпирической физики к аксиоматической.

Понятно, что возможность описывать поведения физических объектов только друг относительно друга и отказ благодаря этому от использования пространственно-временного континуума влечет за собой отказ и от использования понятия действие на отдельные физические объекты, вызывающее изменения поведения их в этом континууме. Это приводит, кроме всего прочего, еще и к тому, что не существует задача одного тела – определение поведения только одного объекта под действием внешних сил, и обратной задачи – определение действующих на объект сил, исходя из его поведения в какой-то системе отсчета. Заметим, что в традиционной эмпирической физике такие задачи существуют и являются основными, можно сказать, определяющими смысл физики. Параллельно с ненужностью понятия действие на отдельные объекты, отпадает необходимость использовать понятие системы отсчета, если оно отличается от понятия физические объекты, и понятие координат каждого объекта в этих системах, если оно отличается от понятия взаимной удаленности объектов. Это означает, что отпадает необходимость постулировать какие-либо законы преобразования координат при переходе к разным системам отсчета. Тем самым, отказ от использования пространственно-временного континуума приводит в соответствие способы описания изменений физических объектов фактически имеющим место способам наблюдения за ними. Это позволяет говорить о физике как о наиболее последовательной и всеобъемлющей науке изучающей природу.

Понятие система отсчета заимствовано из математики, где оно формализовано наиболее строгим образом без упоминания фундаментальных физических характеристик, и широко используется для описания математических объектов. Понятие система отсчета, а также и понятие пространство, возникли на ранних этапах развития естествознания при наблюдениях за явлениями, ограниченными только  земными условиями. При этом явно или неявно предполагается существование абсолютной системы – единой неизменяемой и неподвижной материальной среды, называемой в различные времена эфиром, пространством, субстанцией и др. Первоначально роль такой среды отводилась плоти земли, только относительно которой доступно было наблюдать любое движение каждого земного объекта и каждой системы отсчета. Наблюдения за объектами осуществляемые с помощью разных практически доступных материальных систем отсчета должны в этом случае сопоставляться друг с другом посредством наблюдения за поведением самих этих систем отсчета относительно единой абсолютной системы. В свете выше изложенного, использование понятий систем отсчета, не являющихся физическими объектами, например,  «инерциальных» систем искусственно введенными для наблюдения за физическими объектами, представляется необоснованным, поскольку эти понятия не всегда используются даже при наблюдениях в земных условиях, не говоря уже о внеземных наблюдениях. Мы наблюдаем материальные объекты, как с помощью приборов, так и непосредственно, только относительно других конечных материальных объектов. Поэтому вышеуказанные континуальные понятия эмпирической физики не являются необходимыми для познания природы. «В природе мы познаем собственно только движение, без которого чувственное впечатление невозможно. Все прочие понятия, например геометрические, произведены нашим умом искусственно, будучи взяты в свойствах движений, а потому пространство само собой отдельно для нас не существует». Это мнение геометра – гениального Н. И. Лобачевского, одного из создателей неэвклидовой геометрии, существенно изменившей наши взгляды на естествознание, см. [12], стр. 158.

Поведение систем большого числа (больше четырех) объектов более рационально описывать не набором пространственных удаленностей их друг от друга, как это обсуждалось выше, а с использованием, так называемых пространственных координат, представляющих собой пространственные удаленности этих наблюдаемых физических объектов до объектов какой-то одной другой системы объектов. Эту другую систему объектов будем называть системой отчета или телом отсчета, поскольку любую систему объектов можно представлять как одно тело – один физический объект. Понятно, что желательно, чтобы  эта система сохраняла свои характеристики, или чтобы изменения этой системы были бы несравнимо меньшими, чем изменения описываемой с ее помощью системы объектов. Необходимым и достаточным условие этого является постоянство (малая изменяемость) пространственных удаленностей любых трех ее объектов, т.е. такая система должна быть твердым телом. С учетом этого каждый объект описываемой системы объектов может иметь в такой системе отсчета не более трех однозначно идентифицирующих его пространственных координат, являющихся пространственными удаленностями его до каждого из этих трех взаимно неподвижных объектов системы отсчета. Если для однозначной идентификации каждого физического объекта в системе отсчета необходимы все три координаты, то говорят, что такая система отсчета является трехмерной, что эквивалентно утверждению о том, что описываемые в ней объекты расположены в трехмерном пространстве. Если для идентификации каждого описываемого объекта достаточно лишь двух координат или лишь одной координаты, то такие системы отсчета называют соответственно двумерной и одномерной. При этом в соответствующих случаях говорят, что объекты расположены в двух - и в одно мерных пространствах. С помощью пространственных координат объектов можно в случае необходимости определять и изменения пространственных удаленностей друг от друга любых двух объектов описываемой системы. Число таких пар у систем четырех и большего числа физических объектов намного превышает число самих объектов а, следовательно, и число их координат, чем и объясняется целесообразность использования пространственных координат, а не удаленности объектов друг от друга для описания поведения систем большого числа объектов.

          Для любой наблюдаемой системы объектов, в силу существования выше сформулированной фундаментальной закономерности природы, всегда можно с той или иной точностью найти практически неизменяемый объект (материальное тело), который можно было бы считать телом (системой) отсчета для описываемой системы объектов. Это имеет место, как для астрономических наблюдений, так и для различных земных ситуаций, в частности, для так называемых упругих структур или конструкций. Заметим, что с помощью таких структур в эмпирической физике определяются используемые в ней константы, например, гравитационная постоянная. Имеются в виду так называемые  опыты «по взвешиванию» Земли (опыты Кавендиша (1731-1810)) с помощью «крутильных весов». С тем чтобы исключить разночтения ниже изложенного, формализуем само определение упругих конструкций, совпадающее, по сути, с выше введенным понятием упругие тела, и уточним физический смысл используемых при этом терминов (в частности таких как «упругая связь», «собственные формы, частоты, нагрузка», и др.). Под упругой/деформируемой структурой или конструкцией будем понимать такую систему не менее трех материальных тел, в которой изменение относительной пространственной удаленности каких-нибудь двух из них приводит к изменению относительной удаленности любого другого тела этой системы относительно хотя бы одного из этих двух тел.

При этом говорят, что каждые два таких тела «связаны друг с другом упругой связью»  или упруго действуют друг на друга. Изменение относительной пространственной удаленности упруго связанных тел конструкции называют деформированием ее. В эмпирической физике говорят, что для возможности каких-либо движений/изменений объекта необходимо, чтобы на него (на каждую его часть, движущуюся/изменяющуюся вместе с самим объектом как одно целое) оказывалось какое-либо действие со стороны других объектов. Это действие называют нагрузкой и говорят, что необходимым условием деформирования конструкции является действие на разные ее тела разных нагрузок, в  частности, надо чтобы нагрузки действовали не на все тела конструкции. В упругой конструкции имеет место зависимость между величинами нагрузок и степенью деформирования ее. Если изменение относительной пространственной удаленности каких-нибудь двух и более тел составляющих конструкцию не представляет интерес, то такую систему тел удобнее рассматривать как единую недеформируемую часть конструкции, т.е. рассматривать ее как твердое тело. Каждое твердое тело должно характеризоваться, помимо своих пространственных координат, еще и своими размерами, и поэтому такую часть конструкции иногда называют конечно-размерной массой или конечным элементом. Во многих задачах для идентификации такой массы удобнее задавать дополнительно к пространственным координатам не размеры этой массы, а ее, так называемые угловые координаты, которые могут быть получены путем арифметических операций с пространственными координатами материальных тел составляющих такую массу. Заметим, что угловые координаты используются для идентификации не только конечных, но также и континуальных масс – материальных тел, размеры которых считают бесконечно малыми. Относительные изменения пространственных и угловых координат упруго связанных тел конструкции называются соответственно нормальными и сдвиговыми деформациями ее. Заметим, что принятое определение упругой структуры/конструкции не требуют обязательного представления упругих связей между ее телами как материальных объектов, т.е. объектов имеющих фундаментальные физические характеристики. Это положение имеет место не только для континуальной упругой структуры, ее еще называют упругой средой, т.е. такой для которой нет необходимости или возможности (скорее всего – пока) экспериментально определять значения размеров и относительных удаленностей, соседних друг к другу материальных объектов, составляющих такую среду. Это же положение имеет место и для дискретной упругой структуры, для которой размеры объектов составляющих ее и относительные удаленности всех пар таких объектов являются конечными – способными быть определенными непосредственно опытным путем.  Подчеркнем, что выбор континуального или дискретного представления конкретной упругой структуры является, в конечном счете, сугубо субъективным и это необходимо иметь в виду, и относиться скептически к утверждениям о том, что одно из этих представлений объективно является аппроксимацией (упрощением или приближением) другого представления. Заметим, что необязательность представления упругих связей между телами как материальных объектов может иметь место не только при расчетах строительных или машиностроительных упругих конструкций, но и при рассмотрении других систем объектов, в которых пространственные удаленности объектов тоже «связаны» друг с другом, например, планет солнечной системы или других планетарных систем.

Нагрузки, вызывающие изменения только пространственных или только угловых координат тел, называют соответственно силами или моментами. При этом говорят, что силы вызывают поступательные движения тел, а моменты – вращательные движения (повороты). На каждое тело могут действовать независимые друг от друга, как силы, так и моменты. Как уже указывалось, изменения пространственной удаленности друг от друга двух физических объектов может происходить только при изменении удаленностей от них других объектов, которыми могут быть как внешние, так и внутренние объекты конструкции. При этом можно говорить, что на участвующие в деформировании тела могут действовать соответственно внешние и внутренние нагрузки. Состояния и формы деформирования, которые конструкция приобретает под действием внешних нагрузок, приложенных к каким либо телам ее, иногда называют вынужденными состояниями и формами. В случае если конструкция абсолютно изолирована, т.е. если все тела конструкции имеет постоянные скорости относительно любых внешних объектов, то говорят, что внешние нагрузки на конструкцию отсутствуют, а состояние ее называют естественным, тривиальным или недеформированным (внешними нагрузками). От этого состояния «отсчитывают» любое другое искусственное, нетривиальное, деформируемое состояние, которое конструкция приобретает в случае действия на нее внешних нагрузок, т.е. при не изолированности от нее всех внешних объектов. Изолированная конструкция может иметь так называемые собственные формы деформирования благодаря существованию внутренних нагрузок. Количество таких форм совпадает с числом материальных тел конструкции. Иногда говорят, что собственные формы являются вынужденными формами деформирования, приобретаемыми конструкцией только под действием приложенных к ее телам внутренних нагрузок. Вынужденные и собственные формы деформирования    конструкции могут совпадать друг с другом, и в этом случае говорят, что эти формы конструкция приобретает под действием собственных нагрузок. Понятно, что собственные нагрузки должны быть по величине пропорциональны величинам масс тел, к которым приложены эти нагрузки и собственным формам конструкции. Это будет иметь место, например, если все тела конструкции совершают синхронные колебания относительно тела отсчета или, что тоже, если тело отсчета совершает гармонические колебания относительно конструкции. Частоты таких колебаний называются собственными частотами, а квадраты их являются коэффициентами пропорциональности между собственными формами, умноженными на массы, и собственными нагрузками. Такие собственные нагрузки называют инерционными нагрузками.

То, что в изложенном выше аксиоматическом подходе к физике различные фундаментальные взаимодействия, получаются как следствия априори принятых исходных постулатов, а не как экспериментально установленные факты, приводит к необходимости принципиального пересмотра взгляда на физику и математику как соответственно чисто эмпирическую и аксиоматическую науки. Можно даже сказать, что возникает необходимость пересмотреть взгляд на естествознание как на нечто абсолютно объективное и не зависящее от человека (субъекта), призванного лишь познавать то, что априори создано и существует вне связи с ним. Образно говоря, человечество, являющееся неотъемлемой частью природы, более правильным считать не просто читателем книги под названием «Естествознание», но и соавтором такой книги. Человек является не просто частью природы, а такой частью, без которой не возможно и бессмысленно познания природы. Патетически говоря, создавая природу Создатель пришел к необходимости создания человека для того, чтобы кто-то мог познать и насладиться его гениальным творением. И, не создав, в конце концов, человечество,  вряд ли имело бы смысл, да и возможно было бы заниматься таким творчеством. Пересмотр взглядов на естествознание имеет не только философское, но и сугубо практическое значение, которое не может не оказать существенного влияния на повседневную жизнь, поскольку на основании такого пересмотра могут быть более глубоко познаны существующие и созданы новые технологии.

Как неоднократно указывалось выше, математика и физика имеют одинаковые как идеологию построения, основанную на использовании понятия предшествования, так и конструктивную методологию. Об этом свидетельствует и то, что основное понятие математики – натуральные числа нельзя осмыслить вне понятия физический объект, прочем, как и нельзя, осмыслить понятия физические объекты без понятия натуральные числа. Единство гносеологии математики и физики проявляется также и в том, что фундаментальные математические константы могут определяться путем проведения экспериментов с физическими объектами, как это делается в физике при определении своих констант, например, гравитационной постоянной. В частности, иррациональное число  можно определять с помощью известного физического метода «иглы Бюффона» или, как относительно недавно (в девяностых годах ХХ века) было показано, с помощью так называемого «бильярдного» метода. Причем, точность определения этой константы зависит лишь от числа проводимых опытов. В последнее время все больше становится понятным, что математические вычисления а, следовательно, и любые логические суждения, это всегда некий физический процесс на квантовом уровне. На указанное пытался обратить внимание научного мира еще в 1960 г. американский физик Р. Ландауэр. К сожалению, в то время среди ученых господствовал взгляд на вычисления как на некоторую абстрактную логическую процедуру, изучать которую следует математикам, а не физикам. На эквивалентности математических суждений и физических процессов основывается идея создания в недалеком будущем, так называемого квантового компьютера, отличить который от «человеческого мозга» будет еще труднее (практически невозможно) чем для современных компьютеров. Понятно, что имеется в виду, что еще труднее будет установить такое отличие не при визуальном, а при интерактивном общении человека с компьютером.

В последнее время произошли существенные подвижки во взглядах на естествознание вообще, и на математику – в частности. Вот мнение современного и авторитетнейшего математика - россиянина В. И. Арнольда: «Математика является экспериментальной наукой – частью теоретической физики и членом семейства естественных наук», см. [13].  Исходными объектами математики являются несоставные (математические) объекты, а физики – составные (физические) объекты. Этим объясняется и существование у физических объектов дополнительных характеристик  по сравнению с математическими объектами. Можно сказать, что два такие вида объектов отличаются друг от друга соответственно отсутствием и наличием возможностей наблюдения за изменением количественного состава их, которое приводит к качественным изменениям объектов. Такие изменения могут происходить только при излучении и поглощении объектов, что возможно у физических (составных) объектов и не возможно для математических (несоставных) объектов. В свою очередь, различие возможностей таких наблюдений можно объяснить тем, что для математических объектов эти два события неразличимы (величина предшествования их бесконечна), а для физических объектов – различимы (величина предшествования их конечна). Если использовать физическую терминологию,  то речь может идти о том, что скорость «движения сигнала в математике» бесконечна, а в физике – конечна. Или говоря иначе, интервал времени между событиями «излучения и поглощения» сигнала в математике (для математических объектов) отсутствует, т.е. имеет бесконечные значения, тогда как для различимых событий в физике интервал конечен. Поэтому физические объекты имеют массу и могут изменяться во времени в отличие от математических объектов. Таким образом, математика с этой точки зрения может рассматриваться как предельный случай физики. Более детальное раскрытие единства математики и физики, учитывая колоссальный объем знаний, накопленных этими древнейшими науками, едва ли целесообразно в рамках настоящей статьи.

Аксиоматический подход к построению физики позволяет, как показано выше, существенно упростить ее и продвинуться в решении основных проблем. Например, позволяет отказаться от представления физики в виде двух наук – макро и микрофизики, парадигмы которых основаны соответственно на непрерывности и дискретности физических явлений и поэтому имеющих разные фундаментальные закономерности. Появляется возможность понять, что собой представляют и почему существуют различные виды взаимодействия объектов – гравитационные, электростатические, магнитные, сильные, слабые и др., и благодаря такому пониманию появляется возможность описывать их как проявление одной и той же сущности. Получают объяснение причина существования необратимости физических явлений – причина существования «Стрелы Времени», и другие не вполне ясные в рамках традиционного подхода вопросы, например, существование инерции.

Общеизвестно уже со времен Эвклида, что наибольшие шансы на успех могут иметь лишь аксиоматически (но не эмпирически) построенные теории. Т.е.  теории, построенные исходя из небольшого числа самых общих и очевидных положений, а не теории, основанные только на специальных экспериментально наблюдаемых и часто не связанных между собой, физических явлениях – эмпириях. Именно аксиоматически построенные теории могут считаться, по мнению известного специалиста ХХ века в области философии науки Карла Поппера, хорошими теориями, поскольку они позволяют делать предсказания, которые в принципе не могут быть экспериментально опровергнуты. Традиционная физика, построенная эмпирически,  такой «хорошей» теорией не является и поэтому она вряд ли может иметь позитивные перспективы по сравнению с аксиоматической физикой. Наиболее ясно это понимают сами физики-теоретики, о чем свидетельствует, например, следующее высказывание авторитетного физика ХХ века Стивена Хокинга. «В теоретической физике для продвижения вперед поиск логической последовательности всегда был важнее, чем экспериментальные результаты. Многие прекрасные теории отвергались, т.к. не согласовывались с наблюдениями, но я не знаю, ни одной серьезной теории, которая бы продвинулась только на основе эксперимента. Теория всегда приходит первой, она возникает из желания получить стройную математическую модель», см. [14] стр. 50.

Совершенно очевидно, что переход от эмпирической физики к аксиоматической физике, сколь болезненным в психологическом плане бы он не был, приведет к весьма позитивным практическим результатам, предсказать которые весьма трудно. Как любят шутить физики-теоретики «что может быть более практичнее, чем хорошая теория».

 

ЛИТЕРАТУРА

1.    Картер Б. Совпадение больших чисел и антропологический      принцип космологии//Космология теория и наблюдение.М.,1978.

2.    Начала Евклида, книги 1-V1, перевод. Д. Д. Мордухай-Болтовского, М.–Л., Гостехиздат, 1948.

3.    А. Пуанкаре. О науке, «Наука», М., 1983.

4.    А. В. Погорелов. Основания геометрии, «Наука», М., 1968.

5.    Г. Кантор. К обоснованию учения о трансфинитных множествах, «Наука», М., 1985.

6.    Переписка Лейбница и Кларка. Пятое письмо Лейбница, §45.

7.    Б. Ротгауз. Начала нетрадиционной эволюции физики. Сайт в Интернет  http://rotgauz.narod.ru.

8.    П.Я. Чаадаев, "Статьи и письма", М., изд-во "Современник", 1989 г.

9.    А. Сухотин. Парадоксы науки, М.: «Молодая гвардия», 1980. Электронная версия, дата обновления 3 ноября 2001 года http://n-t.org//ri/sh/pn05.htm.

10.                    Математическая энциклопедия, М., 1977.

11.                    И. Пригожин, И. Стренгенрс. Время, хаос, квант. К решению парадокса времени, «ЭдиториалУРРС» М., 2001.; Порядок из хаоса. Новый диалог человека с   природой, «ЭдиториалУРРС» М., 2001.

12.                    Лобачевский Н.И.. Полн. собр. Соч. т.2, М. – Л., 1949.

13.                    В.И. Арнольд. Математика и математическое образование в современном мире. http://elementy.ru/lib/430178/430281.

14.                    С. Хокинг. Черные дыры и молодые вселенные.      Санкт-Петербург, изд-во Амфора/Эврика,  2001.

15.                    Н. Т. Роузвер. Перигелий Меркурия, от Леверье до Эйнштейна, «Мир», М. 1985.

16.                    Брайан Дэвис (Brian Davies). Куда движется математика? http://elementy.ru/lib/164681/164682

 

Dr. Borys Rotgauz, Merziger Str. 23, 40476 Düsseldorf, Deutschland,

tel. +49(0) 211 9348181,

 E-mail: brotgauz@mail.ru

http://rotgauz.narod.ru/

Последние редакционные изменения 16.11.07

Обсудить в форуме сайта